图像处理与计算机视觉--第五章-图像分割-自适应阈值分割
文章目录
-
- 1.自适应阈值分割介绍
- 2.自适应阈值函数参数解析
- 3.高斯概率函数介绍
- 4.自适应阈值分割核心代码
- 5.自适应阈值分割效果展示
- 6.参考文章及致谢
1.自适应阈值分割介绍
在图片处理过程中,针对铺前进行二值化等操作的时候,我们希望能够将图片相应区域内所有的信息提供保留。实验室环境下,相应的素材是模板化的,但是将实验室方法应用于现实环境中时,我们会发现光影环境对于效果的影响其实是很大的。在这种情况下进行处理,会使得结果不如人意:一块黑,一块白,且黑的区域的特征无法提取。这时候自适应阈值算法尤为重要。与全局阈值不同,它更加注重上下文关系,将原本图片分割成更小的区域进行判断,极大地降低了阴影对于图片本身的影响。
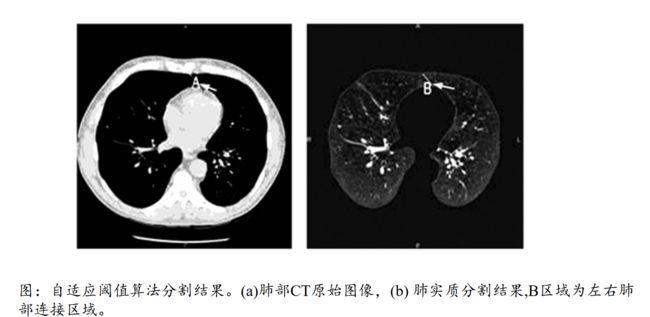
自适应阈值用于二值化处理图像,具有比较好的处理效果,相比对全阈值处理方法,自适应阈值中的每一个像素点的阈值都不是固定相同的,而是由其领域中的图像像素点加权平均计算而得到的,这样的处理方法有如下好处:
1.每个像素位置处的二值化阈值不是固定不变的,而是由其周围邻域像素的分布来决定的。
2.亮度较高的图像区域的二值化阈值通常会较高,而亮度较低的图像区域的二值化阈值则会相适应地变小。
3.不同亮度、对比度、纹理的局部图像区域将会拥有相对应的局部二值化阈值,这样处理出的图像效果更加明显。
2.自适应阈值函数参数解析
在Opencv库函数中,给出了自适应阈值分割的函数如下所示:
fig1 = cv2.adaptiveThreshold(src, maxValue, adaptiveMethod, thresholdType, blockSize, C, dst=None)
接下来我将具体解释adaptiveThreshold()中各个参数的意义,如下所示:
"""
fig=cv2.adaptiveThreshold(src, maxValue, adaptiveMethod, thresholdType, blockSize, C, dst=None)
参数解释:
1.src:原图像,就是你需要进行自适应阈值分割处理的图像
2.maxValue:最大像素点,其含义表示如果某点的像素值大于对应的阈值,那么将像素值取为255.
3.adaptiveMethod:计算阈值的方法,Opencv中包括了两种:1.cv.ADAPTIVE_THRESH_MEAN_C:计算出领域的平均值作为阈值。
2.DAPTIVE_THRESH_GAUSSIAN_C:计算出领域的高斯均值作为阈值。
4.thresholdType:取值类型,只有两个取值:1.THRESH_BINARY 2.THRESH_BINARY_INV
5.blockSize:计算单位是像素的邻域块大小选择,这是局部邻域大小,只能取奇数,如3/5/7/9/11等
6.C:阈值偏移量,正负数都可以,所以阈值的大小=C+adaptiveMethod计算出的阈值值
"""
3.高斯概率函数介绍
高斯分布是人工智能方面很常见的一种概率分布函数,常见的一维高斯概率密度分布函数如下所示:
p ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 p(x)=\frac1{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} p(x)=σ2π1e−2σ2(x−μ)2
在高斯分布函数中,我们可以随意调节标准差 σ \sigma σ和 μ \mu μ的值,来进行高斯分布的变换,如下所示:
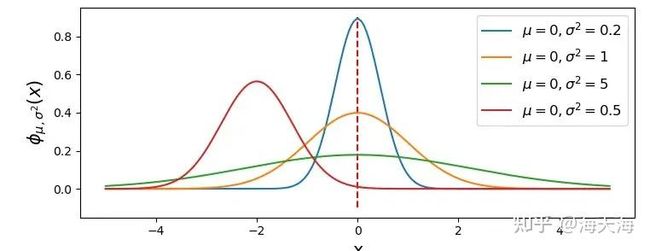
在图像处理中,我们一般用到二维的高斯概率分布函数,如下所示:
f ( x , y ) = ( 2 π σ 1 σ 2 1 − ρ 2 ) − 1 e x p [ − 1 2 ( 1 − ρ 2 ) ( ( x − μ 1 ) 2 σ 1 2 − 2 ρ ( x − μ 1 ) ( y − μ 2 ) σ 1 σ 2 + ( y − μ 2 ) 2 σ 2 2 ) ] f\left(x,y\right)=\left(2\pi\sigma_{1}\sigma_{2}\sqrt{1-\rho^{2}}\right)^{-1}exp\left[-\frac{1}{2\left(1-\rho^{2}\right)}\left(\frac{\left(x-\mu_{1}\right)^{2}}{\sigma_{1}^{2}}-\frac{2\rho\left(x-\mu_{1}\right)\left(y-\mu_{2}\right)}{\sigma_{1}\sigma_{2}}+\frac{\left(y-\mu_{2}\right)^{2}}{\sigma_{2}^{2}}\right)\right] f(x,y)=(2πσ1σ21−ρ2)−1exp[−2(1−ρ2)1(σ12(x−μ1)2−σ1σ22ρ(x−μ1)(y−μ2)+σ22(y−μ2)2)]
当我们令 σ 1 \sigma_{1} σ1= σ 2 \sigma_{2} σ2= σ \sigma σ,同时将 μ \mu μ和 ρ \rho ρ置为0,得出的高斯概率函数如下所示:
g ( x , y ) = 1 2 π σ 2 e − ( x 2 + y 2 ) 2 σ 2 g(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{(x^2+y^2)}{2\sigma^2}} g(x,y)=2πσ21e−2σ2(x2+y2)
高斯概率函数是相对于二维坐标产生的,其中(x,y)为点坐标,要得到一个高斯滤波器模板,应先对高斯函数进行离散化,将得到的值作为模板的系数。例如:要产生一个33的高斯滤波器模板,以模板的中心位置为坐标原点进行取样,模板在各个位置的坐标,如下图所示(x轴水平向右,y轴竖直向下)
标准差 σ =1.3 的 33 的整数形式的高斯滤波器如下:
K = 1 16 ⋅ [ 1 2 1 2 4 2 1 2 1 ] K=\dfrac{1}{16}\cdot\begin{bmatrix}1&2&1\\2&4&2\\1&2&1\end{bmatrix} K=161⋅ 121242121
标准差σ的值可以任意选取,如果σ较小,那么生成的模板的中心系数较大,而周围的系数较小,这样对图像的平滑效果就不是很明显;反之,σ较大,则生成的模板的各个系数相差就不是很大,比较类似均值模板,对图像的平滑效果比较明显,不管选择什么 σ值,我们构建3*3高斯核的时候要确保这九个点加起来为1,从而得到最终的高斯模板。
4.自适应阈值分割核心代码
import cv2
import numpy as np
from matplotlib import pyplot as plt
# 支持中文
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
def adaptiveThreshold_test():
img = cv2.imread(r'C:\Users\Zeng Zhong Yan\Desktop\py.vs\Mechine Learning\lena.jpg',0)#读入图片
img = cv2.medianBlur(img, 5)#中值滤波来处理图像
#图像切割
#全图像二值化/全局阈值法处理图像
ret, th1 = cv2.threshold(img, 127, 255, cv2.THRESH_BINARY)
#平均值计算阈值方法(cv2.ADAPTIVE_THRESH_MEAN_C)-偏移值
th2 = cv2.adaptiveThreshold(img, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, 11, 2)
#高斯值计算阈值方法(cv2.ADAPTIVE_THRESH_GAUSSIAN_C)-偏移值
th3 = cv2.adaptiveThreshold(img, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, 11, 2)
#图像可视化绘制
titles = [u'原始图像', u'全局阈值处理图像',u'自适应平均阈值处理图像', u'自适应高斯阈值处理图像']
images = [img, th1, th2, th3]
for i in range(4):
plt.subplot(2, 2, i + 1), plt.imshow(images[i], 'gray')
plt.title(titles[i])
plt.xticks([]), plt.yticks([])
plt.show()
if __name__ == '__main__':
adaptiveThreshold_test()
5.自适应阈值分割效果展示
6.参考文章及致谢
本章内容的完成离不开大佬文章的启发和帮助,在这里列出名单,如果对于内容还有不懂的,可以移步对应的文章进行进一步的理解分析。
1.自适应阈值图像切割:https://blog.csdn.net/weixin_43977647/article/details/115354680?spm=1001.2014.3001.5502
如果大家这这篇blog中有什么不明白的可以去他的专栏里面看看,内容非常全面,应该能够有比较好的解答。
在文章的最后再次表达由衷的感谢!!

