归并排序详解(递归+非递归)
目录
归并排序
归并排序的思想
递归实现
非递归实现
归并排序
归并排序和之前讲的快速排序、希尔排序、堆排序一样,时间复杂度是O(N*logN)。
它相对难理解一点,接下来我就从递归以及非递归两个方面详细介绍一下这种排序。
归并排序的思想
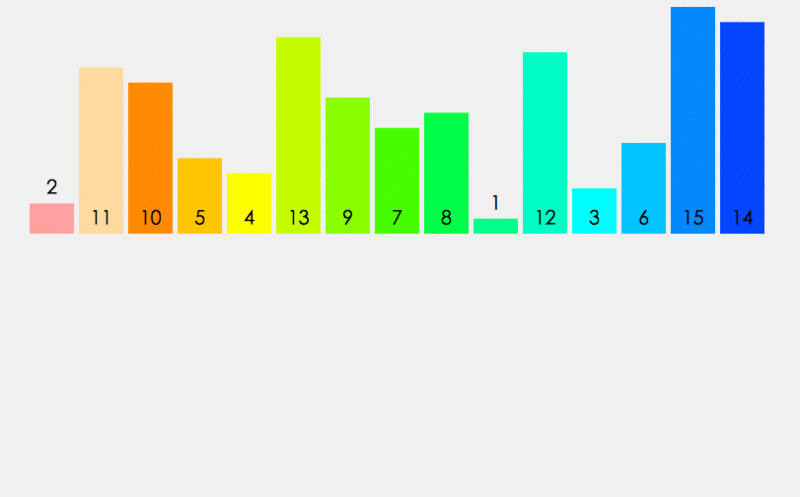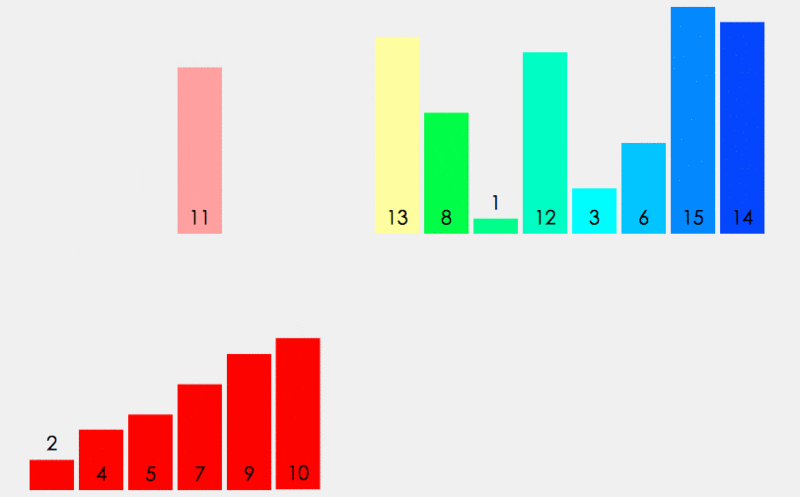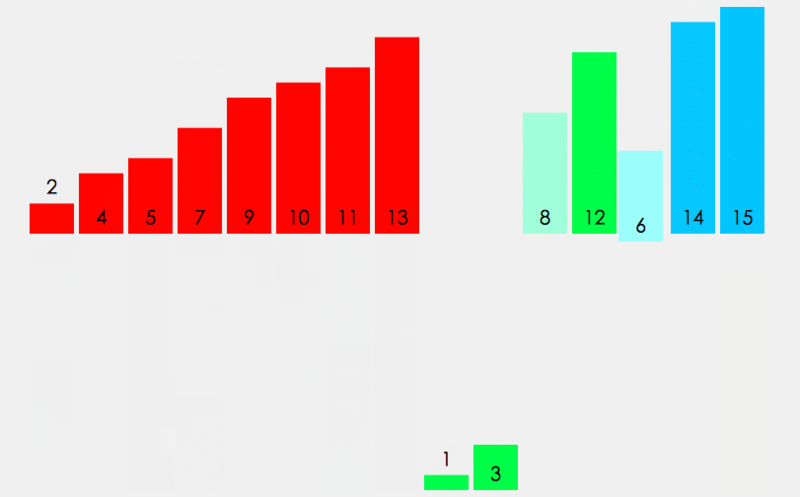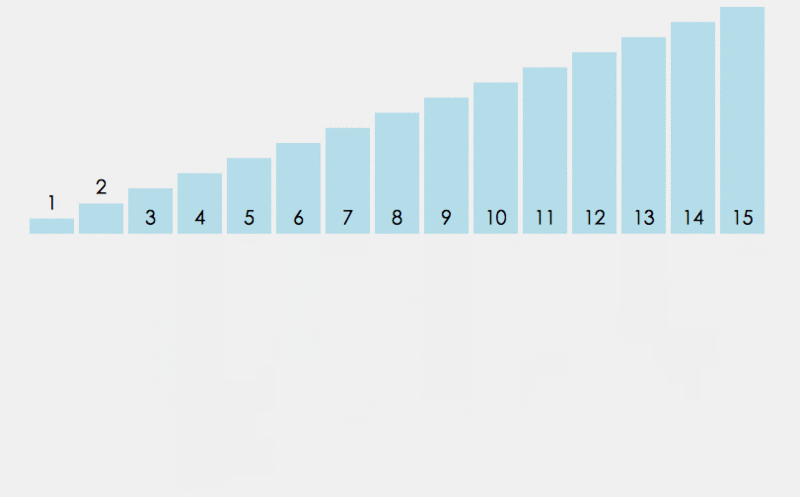
一个数组从中间将其分为左右两个区间,如果左右区间都是有序的,那么就可以进行归并,分别从两个区间取小的数尾插到新开辟的数组中,不断取小的尾插直到排完。
那么如果两个区间没有序呢?—— 那就再将这个问题划分子问题,左区间进行上述操作,右区间也进行上述操作......一直分治下去,直到左右区间只剩一个数,就划分为最小子问题,无需再往下分了,这个过程也就是递归的过程。
这就是归并排序的思想,划分子问题,分而治之。
递归实现
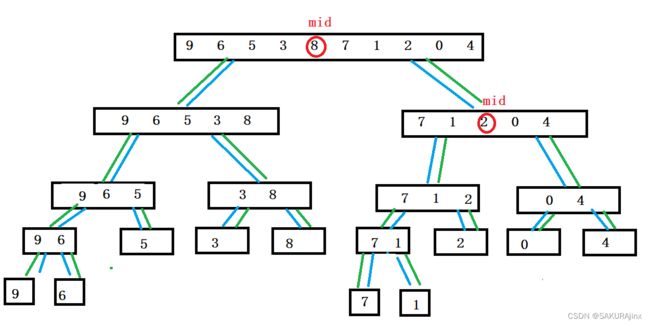
假设有一个数组a[10] ={9,6,5,3,8,7,1,2,0,4} 要将它排成升序,可以先找出数组的中间位置,将数组从中间分开,划为两个区间,分别将两个区间排成有序的。
那如何将这两个区间排成有序的呢?————再重复上面步骤分别划分左右两个区间,再将其排成有序的,重复上述步骤......直到左右区间都分的只剩一个数,那也就可以认为它是有序的。整个过程就是一个递归调用的过程。
大家觉得这个递归过程像什么呢? 是不是有点像二叉树。这里的归并递归过程有点类似二叉树里面求树的高度,先递归计算左右子树的高度,都是用的后序遍历。
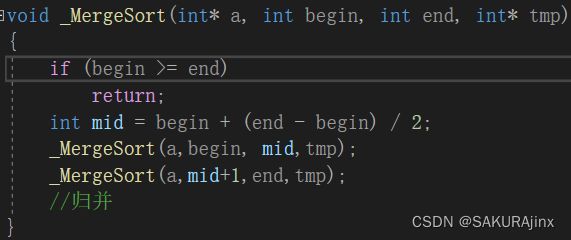
先将大体框架完成一下:
void _MergeSort(int* a, int begin, int end,int* tmp)
{
if (begin >= end)
return;
int mid = begin + (end - begin) / 2;
_MergeSort(a,begin, mid,tmp);
_MergeSort(a,mid+1,end,tmp);
//归并
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
_MergeSort(a, tmp, 0, n-1);
free(tmp);
tmp = NULL;
}
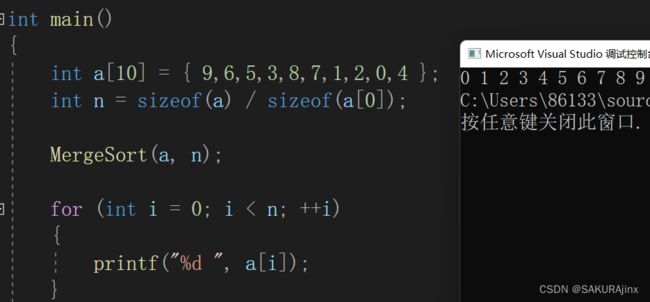
int main()
{
int a[10] = { 9,6,5,3,8,7,1,2,0,4 };
int n = sizeof(a) / sizeof(a[0]);
MergeSort(a, n);
for (int i = 0; i < n; ++i)
{
printf("%d ", a[i]);
}
return 0;
}归并排序一般用两个子函数,这样方便一些。
先计算中间位置,得出左右区间,对左右区间递归排序,直到各自只剩一个数时返回。
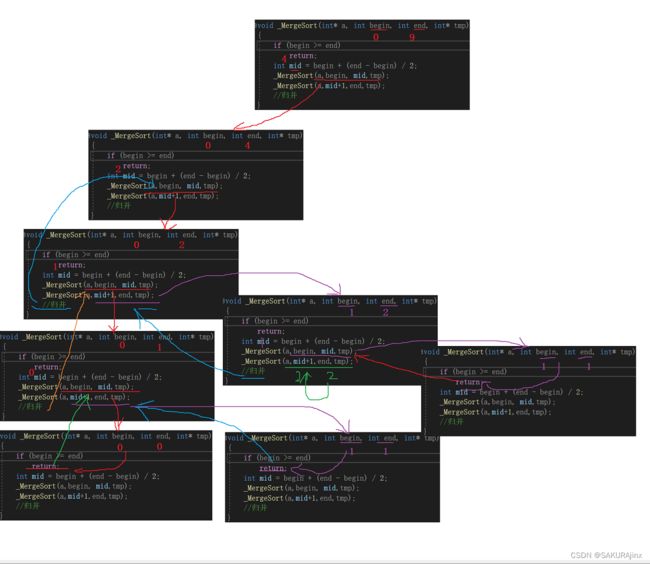
上面是局部递归展开图(归并过程没写),可借助展开图来理解递归过程。
接下来实现归并细节。
依据上图,先将左右区间的边界值表示出来:左区间 [begin,mid] 右区间 [mid+1,end]
找到每一组里面小的那个数,尾插到新开辟出的数组里,不断地取小的尾插,尾插一次就memcpy拷贝回原数组。
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
return;
int mid = begin + (end - begin) / 2;
_MergeSort(a,begin, mid,tmp);
_MergeSort(a,mid+1,end,tmp);
//归并
int i = begin;
int begin1 = begin, end1 = mid,
begin2 = mid + 1, end2 = end;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}时间复杂度:O(N*logN), 递归深度为logN,每一层递归因为要遍历选小的数,所以是O(N),合起来就是O(N*logN)
空间复杂度:O(N),开辟了额外的tmp空间,这里不及快排,快排空间复杂度是O(logN)
非递归实现
在深度了解递归的情况下,我们也可以用非递归来实现。非递归实现还是有一定难度的,不太好理解,建议将递归展开图多画画,吃透了再实现非递归。
归并排序的非递归,我们不借助栈或队列等结构实现,直接用迭代手撕。
其本质和递归异曲同工,只是用循环完整的呈现了全部过程。
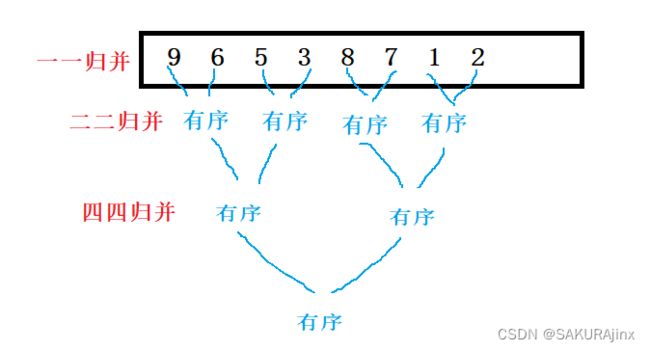
递归方法是一路往下走,到最底层只剩一个数归并,返回上一层有两个数,两两归并,依次往上返回。这里非递归相当于是反过来了,最开始一一归并,然后将有序的两两归并.......
大体思路简单,但是控制边界值挺麻烦,先实现大框架:
我们要一开始一一归并,再两两归并.......可以设定一个gap,让它一开始为1,每归并完一层就*2,
就可以实现控制了。
void MergeSortNon(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int j = 0; j < n; j += gap * 2)
{
int i = j;
int begin1 = j, end1 = j + gap - 1,
begin2 = j + gap, end2 = j + 2 * gap - 1;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
gap *= 2;
memcpy(a, tmp, sizeof(int) * n);
}
}
free(tmp);
tmp = NULL;
}注意这里begin1 ,end1,begin2,end2的初始值。对照着图可以推出来。
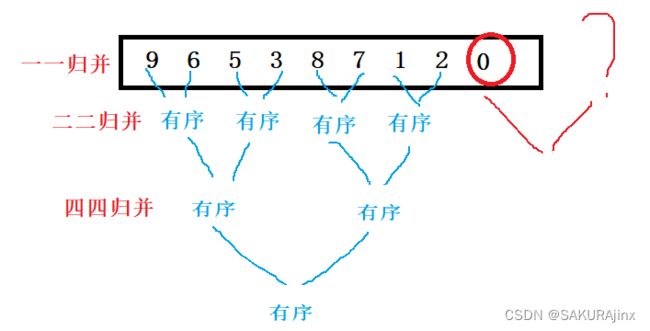
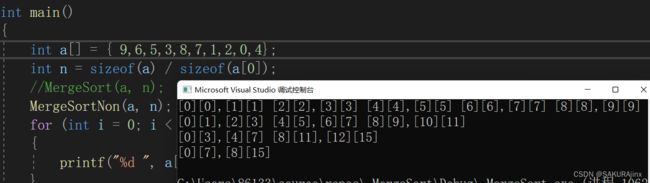
这是基本框架,但是注意:上面数组里面个数正好为8,是2^3,当数组个数不是2^n时,情况就完全不同了。
比如个数为9,10时,如图:
比如这样两种情况就会出现问题。
以左图为例,对照代码看:当gap = 4时,j = 8,begin2 = 9,end2 = 9 越界了。
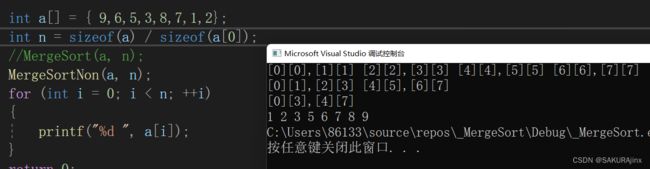
同理,右边也一样,其他情况下也会产生越界。为了方便观察什么情况下会越界,我们加入打印。
int i = j;
int begin1 = j, end1 = j + gap - 1,
begin2 = j + gap, end2 = j + 2 * gap - 1;
printf("[%d][%d],[%d][%d] ", begin1, end1, begin2, end2);当数组元素个数为2^n 时
当数组元素个数为奇数个时
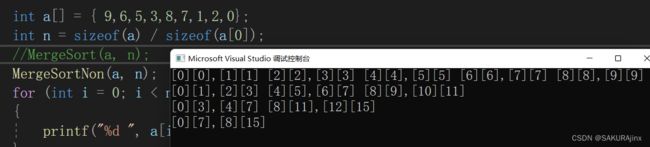
当数组元素个数是偶数个但不为2^n 时
根据上图,我们把越界情况分为三种:
1、第一组end1越界
2、第二组begin2,end2全部越界
3、第二组end2越界
针对上述三种情况进行修正,就可以避免越界实现非递归。
如果拷贝的地方是像上面一样全部归并完了再拷贝的,那就比较麻烦了。因为中间可能会拷回去越界的随机值,所以需要一一修正边界,不推荐这种拷贝方式。
可以将拷贝放到循环里,归并多少数据就拷贝多少数据,就不会产生越界拷贝随机数的情况了,也不需要一一修正边界。
如果是第一组end1越界,那他后面也不需要归并了,直接break出去就行。
如果是第二组begin2,end2全部越界,那也是一样,说明不需要归并,也直接break即可。
如果是第二组end2越界,那end2前面一个数还需要归并,此时修正一下end2,改成n-1。
void MergeSortNon(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int j = 0; j < n; j += 2 * gap)
{
int begin1 = j, end1 = j + gap - 1,
begin2 = j + gap, end2 = j + 2 * gap - 1;
int i = j;
//第一组end1越界
if (end1 >= n)
{
printf("[%d][%d]", begin1, n - 1);
break;
}
//第二组全部越界
if (begin2 >= n)
{
printf("[%d][%d]", begin1, end1);
break;
}
//第二组end2越界
if (end2 >= n)
{
printf("[%d][%d]", begin2, n - 1);
//修正end2,继续归并
end2 = n - 1;
}
printf("[%d][%d],[%d][%d] ", begin1, end1, begin2, end2);
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//归并哪一段,拷贝哪一段
memcpy(a + j, tmp + j, sizeof(int) * (end2 - j + 1));
}
printf("\n");
gap *= 2;
}
free(tmp);
tmp = NULL;
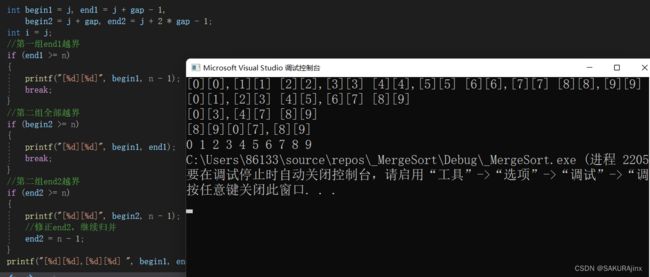
}为了方便观察,这里添加几个打印
是不是和之前画图分析的过程一样呢。这就是非递归的玩法。
如果是一次拷贝的修正边界值,麻烦一点,大家可以去尝试一下。