算法学习笔记（代码随想录，JS语言）

前提：

1.库函数:
如果题目关键的部分直接用库函数就可以解决，建议不要使用库函数。
如果库函数仅仅是 解题过程中的一小部分，并且你已经很清楚这个库函数的内部实现原理的话，那么直接用库函数。

一、数组

一、数组的特点：

1.下标从0开始
2.储存的内存的空间地址是连续的，因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。
3.不能直接删除只能覆盖元素

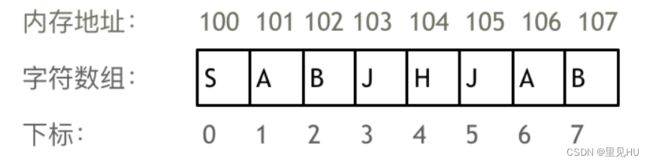
补充：
在c++中二维数组的内存地址也是连续的
在Java中二维数组的内存地址不是连续的（列表映射的方法）

1.二分法

适用：数组是有序排列的
特点：1.左右闭合 2.左闭右开（右开的情况下就不要将每次让right==middle时，不让middle进行计算和比较）

1.1搜索插入位置

核心：
1.在目标值没有的时候应该初始化为数组的长度后进行添加（升序）
2.不断的在小于等于的区间赋值位置的坐标值

var searchInsert = function(nums, target) {
   let l = 0,r = nums.length - 1,n=nums.length
   while(l <= r){
       let mid = parseInt((l+r)/2)
       if(target > nums[mid]){
           l = mid+1
       }else if(target <= nums[mid]){
        //    只需要记录右值也就是插入的中间位置
           n = mid
           r = mid-1
       }
   }
   return n
};

1.2x的平方根

var mySqrt = function(x) {
    let left = 0, right = x,ans=0
    while(left <= right){
        let mid = parseInt((right+left)/2)
        if(mid*mid <= x){
            ans = mid
            left = mid + 1
        }else {
            right = mid - 1
        }
    }
    return ans
};

1.3在排序数组中查找元素的第一个和最后一个位置

核心：1.找到一个不包含目标元素的左右边界 2.利用二分法查找左右边界 3.三种再数组中的情况要考虑清楚
情况一：target 在数组范围的右边或者左边，例如数组{3, 4, 5}，target为2或者数组{3, 4, 5},target为6，此时应该返回{-1, -1}
情况二：target 在数组范围中，且数组中不存在target，例如数组{3,6,7},target为5，此时应该返回{-1, -1}
情况三：target 在数组范围中，且数组中存在target，例如数组{3,6,7},target为6，此时应该返回{1, 1}

//  核心：1.找到一个不包含目标元素的左右边界 2.利用二分法查找左右边界 3.三种再数组中的情况要考虑清楚
var searchRange = function (nums, target) {
    // 1.元素数组之外（左右边界都等于负数）
    //    两个边界函数
    const left = function(nums, target) {
        let leftboder = -2
        let l = 0, r = nums.length - 1
        while (l <= r) {
            let mid = parseInt((l + r) / 2)
            if (target <= nums[mid] ) {
                r = mid - 1
                leftboder = r
            } else {
                l = mid + 1
            }

        }
        return leftboder
    }
   const right = function(nums, target) {
        let rightboder = -2
        let l = 0, r = nums.length - 1
        while (l <= r) {
            let mid = parseInt((l + r) / 2)
            if ( target < nums[mid]) {
                r = mid - 1
            } else {
                l = mid + 1
                rightboder = l
            }

        }
        return rightboder
    }
    let leftboder = left(nums, target)
    let rightboder = right(nums, target)
    //    三种情况的判断
    // 第一种情况
    if (leftboder === -2 || rightboder === -2) return [-1, -1]
    // 第三种情况
    if (rightboder - leftboder > 1) return [leftboder + 1, rightboder - 1]
    // 第二种情况
    return [-1, -1]

};

1.4有效的完全平方根数

//  就是求这个数字的平方根 和x的平方根一样的道理，在[0,num]寻找中间值等于x
var isPerfectSquare = function(num) {
    let l = 0 ,r = num 
    while(l <= r){
        let mid = parseInt((l+r)/2)
        if(mid*mid < num){
            l = mid + 1
        }else if(mid*mid > num) {
            r = mid - 1
        }else{
            return true
        }
    }
    return false
};

2.移除元素(双指针)

• 数组中的内存保存是连续的，因此移动一个元素，其他的元素都要跟着改变，在原地更改的情况下，使用双指针

//  数组中原地移除val的元素（指针）
//  快指针寻找不是val得值，慢指针进行记录
var removeElement = function(nums, val) {
    let k = 0 //初始化记录值
    for(let i = 0;i < nums.length; i++){
        if(nums[i] != val){
            // 原地进行更改
            nums[k++] = nums[i]
        }
    }
    // k值就是num数组的长度
    return k
};

2.1删除排序数组中的重复项

// 关键：fast去过滤去重的数字， slow记录去重的数字

// 关键：fast去过滤去重的数字， slow记录去重的数字
var removeDuplicates = function(nums) {
    let slow = 1,fast = 1  //这里不用考虑第一个
    while(fast < nums.length){
        if(nums[fast] != nums[fast-1]){
            nums[slow] = nums[fast]
            slow++
        }
        fast++
    }
    return slow //输出新的长度那就是slow的值
};

2.2移动零

关键：原地数组进行操作（双指针，快指向非0，慢指向0，符合这两个条件后依次进行交换，否则继续进行比较）

//  容易想到依次循环判断是否为0 以空数组进行存储变量，后面补零即可
//  1.移动0到末尾
// 2.保持非零元素额相对顺序
// 3.原地数组进行操作（双指针，快指向非0，慢指向0，符合这两个条件后依次进行交换，否则继续进行比较）
var moveZeroes = function(nums) {
    let slow = 0,fast = 0
    while(fast < nums.length){
        if(nums[fast] != 0){
            if(nums[slow] == 0){
                 [nums[slow],nums[fast]] = [nums[fast],nums[slow]] 
            }
             slow++    
        }
        fast++
    }
};

2.3 比较含退格的字符串

关键：1.两个指针遍历 2.退格计数器 3.根据计数器去移动指针 4.一次次的根据指针去判断两个俩个字符串

var backspaceCompare = function(s, t) {
    // 初始化变量
    let i = s.length -1,j = t.length -1,skipS = 0,skipT = 0
    // 大循环
    while(i >= 0 || j >= 0){
        // s的循环
        while(i>= 0){
            if(s[i]=="#"){
                skipS++
                // 指针向前移动
                i--
            }else if(skipS > 0){
                skipS--
                i--
            }else {
                break
            }
        }
        // t的循环
        while(j >= 0){
            if(t[j]=="#"){
                skipT++
                j--
            }else if(skipT > 0){
                skipT--
                j--
            }else{
                break
            }
        }
        // 两个参数进行比较，有一个不一样则退出
       if(s[i] != t[j])  return false
       i--
       j--
    }
    // 如果大循环里面的依次遍历全部相等话就为真
    return true
};

拓展：因为else if会判断在它上面的if或else if是否满足条件，如果满足条件，不管else if是否满足条件，都不会执行。只有else if上面的if或者else if不满足条件，才会进行判断

2.4有序数组的平方

//  非递减那么就是升序,这个数组是升序
// 思路：双指针从外向内进行比较
// 1.数组两个边界最大的值排序到后面
// 2.新数组记录最大的值
// 3.从外向内
var sortedSquares = function(nums) {
    let n = nums.length-1
    let arr = new Array(n).fill(0)
    let x = n
    let left = 0, right = n
    while(left <= right){
        if(nums[left]*nums[left] > nums[right]*nums[right]){
            arr[x--] = nums[left]*nums[left]
            left++
        }else {
            arr[x--] = nums[right]*nums[right]
            right--
        }
    } 	
    return arr
};

3.滑动窗口

最大滑窗是在迭代右移右边界的过程中更新结果，而最小滑窗是在迭代右移左边界的过程中更新结果。
最小窗口长度

while j < len(nums):
    判断[i, j]是否满足条件
     j += 1
    while 满足条件：
        不断更新结果(注意在while内更新！)
        i += 1 （最大程度的压缩i，使得滑窗尽可能的小）

最大滑动窗口

while j < len(nums):
    判断[i, j]是否满足条件
      j += 1
    while 不满足条件：
        i += 1 （最保守的压缩i，一旦满足条件了就退出压缩i的过程，使得滑窗尽可能的大）
    不断更新结果（注意在while外更新！）
  

3.1长度最小的子数组

//  滑动窗口
// 符合>= target 的最小子数组的长度
// 1.暴力：两层循环，依次去挨个查找然后找出最小长度
// 2.滑动窗口，如果满足条件后就会持续的更新（这道题是通过sum减值去更新窗口）
var minSubArrayLen = function (target, nums) {
    let slow = 0, fast = 0, sum = 0, res = nums.length + 1
    while (fast < nums.length) {
        sum += nums[fast++]
        while (sum >= target) {  //滑动窗口的缩小不是符合条件一次就好，而是滑动多次去更新这个值,
        // 而且先要记录符合的长度，再去动态的缩小
            res = res < fast - slow ? res : fast - slow //结果值不是自己加的。而是滑动窗口的长度
            sum -= nums[slow++]  //滑动窗口的核心
        }
    }
    return res > nums.length ? 0 : res//不存在的话也就是遍历结束没有符合长度大于了最大数组值
};

$3.2水果成篮

白话题意：求满足某个条件（数组值最多就两类的连续数组，例如[1,2,2,1,2]）的最长数组长度

$3.3最小覆盖字串(困难)

4.螺旋矩阵

4.1顺时针打印矩阵/螺旋矩阵

//  四条边界
// 1.四条边顺序打印结束之后  2.向内缩进  3.缩进条件为对应的边界  重点是先减了边界后再去对比
var spiralOrder = function (matrix) {
    let left = 0, right = matrix[0].length - 1, top = 0, bottom = matrix.length - 1
    let arr = [], x = 0
    while (true) {
        // 从左向右打印
        for (let i = left; i <= right; i++) {
            arr[x++] = matrix[top][i]
        }
        if (++top > bottom) break
        // 从上向下打印

        for (let i = top; i <= bottom; i++) {
            arr[x++] = matrix[i][right]
        }
        if (--right < left) break
        // // 从右到左
        for (let i = right; i >= left; i--) {
            arr[x++] = matrix[bottom][i]
        }
        if(--bottom < top) break
        // 从下到上打印
        for (let i = bottom; i >= top; i--) {
            arr[x++] = matrix[i][left]
        }
        if (++left > right) break

    }
    // 这四个break就是其中有一个不符合条件就退出
    return arr
};

4.2螺旋矩阵2

var generateMatrix = function(n) {
    let left = 0 , right = n-1, top = 0, bottom = n -1
    let  x = 0, y = 1
    let arr = new Array(n).fill(0).map(()=>new Array(n).fill(0))
    while(true){
        for(let i = left; i <= right ; i++){
            arr[top][i] = y++
        }
        if(++top > bottom) break
        for(let i = top; i <= bottom ; i++){
            arr[i][right] = y++
        }
        if(--right < left) break
        for(let i = right; i >= left ; i--){
            arr[bottom][i] = y++
        }
        if(--bottom < top) break
        for(let i = bottom ; i >= top ; i--){
            arr[i][left] = y++
        }
        if(++left > right) break
    }
    return arr
};

二、链表

初始化链表：

class ListNode {
  val;
  next = null;
  constructor(value) {
    this.val = value;
    this.next = null;
  }
}

1、初始化一个空结点，没有复制，指针指向list

    ListNode list=new ListNode();

2、初始化一个空结点，初始值为0，指针指向为list

    ListNode list=new ListNode(0);

3、初始化一个空结点，初始赋值为0，并且list的下一个next指针指向head，指针指向为list

    ListNode list=new ListNode(0,head);

链表是一种通过指针串联在一起的线性结构，每一个节点由两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向null（空指针的意思）。链接的入口节点称为链表的头结点也就是head。

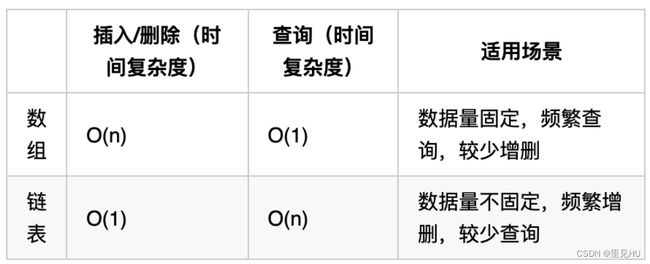
1.移除链表元素

var removeElements = function(head, val) {
    // 为了让头指针一样操作删除，设置一个虚拟的头指针指向它
    let pre = new ListNode(0,head)
    let cur = pre
    while(cur.next){
        if(cur.next.val == val){
            cur.next = cur.next.next
        }else {
            // 不是目标元素就直接移动cur
            cur = cur.next
        }
    }
    return pre.next
};

2.设计链表

详细参考题解回答：Steven Lee

• 单链表中的节点应该具有两个属性：val 和 next。val 是当前节点的值，next 是指向下一个节点的指针/引用。如果要使用双向链表，则还需要一个属性 prev 以指示链表中的上一个节点。假设链表中的所有节点都是 0-index 的。
• 实现功能
  get(index)：获取链表中第 index 个节点的值。如果索引无效，则返回-1。
  addAtHead(val)：在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
  addAtTail(val)：将值为 val 的节点追加到链表的最后一个元素。
  addAtIndex(index,val)：在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度，则该节点将附加到链表的末尾。如果 index 大于链表长度，则不会插入节点。如果index小于0，则在头部插入节点。
  deleteAtIndex(index)：如果索引 index 有效，则删除链表中的第 index 个节点。
• 对于js来说，链表是一种全新的数据类型，我们首先应该先了解其定义才能去实现它。
  1.链表对象
  如果将链表用js对象表示，那它应该具有的最基本的几个属性：
  length 链表长度
  start 头部节点/起始节点
  目前MyLinkedList就是一个空的链表对象

var MyLinkedList = function () {
  let length = 0
  let start = null
};

2.初始化链表节点
因为js没有原生支持链表，所以创建一个节点我们也需要写个方法，把它new出来。一个链表节点能有什么东西呢？只有两个很简单的属性：
val 当前节点的数值
next 下一个节点指向（也可以理解为一个指针）
prev

MyLinkedList.prototype.node = function (val) {
  this.val = val
  this.next = null
  this.prev = null
}

3.获取某一个链表节点的值
因为链表对象无法直接通过下标的方式获取（数组的第3位这种），链表要想获取第N位的值，只能从头部节点向后一个节点一个节点的查找直到找到对应的节点。
要实现的get方法就是传入一个索引，获取对应索引的链表节点的val。

MyLinkedList.prototype.get = function (index) {
  if (index < 0 || index >= this.length) return -1
  let current = this.start
  while (0 < index) {
    current = current.next
    index--
  }
  return current ? current.val : -1 //对于索引位溢出的情况直接返回了-1
}

4.链表头部插入
想要头部插入一个节点，思路很简单，首先将要插入的节点的next（下一节点）指向当前链表的起始节点，然后再将当前链表的起始节点指向插入的头部节点，最后将链表的length++即可实现。

MyLinkedList.prototype.addAtHead = function (val) {
  let tempNode = new this.node(val) //要想给链表插入节点，首先需要new一个节点，传入该节点的val即可实现。
  tempNode.next = this.start || null
  this.start = tempNode
  this.length++
}

5.链表尾部插入
和头部插入节点很像，我们只需要多一步操作：找到最后一个节点即可。
通过判断节点是否含有next节点可以判断当前节点是不是最后一位，如果是最后一位直接插入到最后一位节点之后即可。

MyLinkedList.prototype.addAtTail = function (val) {
  let tailNode = new this.node(val)
  let tempNode = this.start
  while (tempNode && tempNode.next) {
    tempNode = tempNode.next
  }
  if (tempNode) {
    tempNode.next = tailNode
  } else {  //如果开始为空的情况 直接让插入的尾节点当做头结点，头指针指向这个新加的头结点
    tempNode = tailNode
    this.start = tailNode
  }

  this.length++
};

6.链表任意插入
1.初始化节点cur2.将 cur 的 next 字段链接到 prev 的下一个结点 next3.将 prev 中的 next 字段链接到 cur 。

MyLinkedList.prototype.addAtIndex = function (index, val) {
  if (index <= 0) return this.addAtHead(val)
  if (index === this.length) return this.addAtTail(val)
  if (index > this.length) return

  let addNode = new this.node(val)
  let cur = this.start

  while (index-- > 1) {
    cur = cur.next
  }
  addNode.next = cur.next
  cur.next = addNode
  this.length++
};

7.链表任意位置删除
1.找到 cur 的上一个结点 prev 及其下一个结点 next 2.接下来链接 prev 到 cur 的下一个节点 next 。

MyLinkedList.prototype.deleteAtIndex = function (index) {
  if (index < 0 || index >= this.length) return
  if (index) {
    let i = 1
    let cur = this.start
    while ((index - 1) >= i) {
      cur = cur.next
      i++
    }
    if (cur && cur.next) {
      cur.next = cur.next.next
    }
    this.length--

  } else {
    this.start = this.start.next
    this.length--
  }
}

完整版

var MyLinkedList = function () {
  let length = 0
  let start = null
};

MyLinkedList.prototype.node = function (val) {
  this.val = val
  this.next = null
  this.prev = null
  return this
}

MyLinkedList.prototype.get = function (index) {
  if (index < 0 || index >= this.length) return -1
  let current = this.start
  while (0 < index) {
    current = current.next
    index--
  }
  return current ? current.val : -1
}

MyLinkedList.prototype.addAtHead = function (val) {
  let tempNode = new this.node(val)
  tempNode.next = this.start || null
  this.start = tempNode
  this.length = this.length ? ++this.length : 1
};

MyLinkedList.prototype.addAtTail = function (val) {
  let tailNode = new this.node(val)
  let tempNode = this.start
  while (tempNode && tempNode.next) {
    tempNode = tempNode.next
  }
  if (tempNode) {
    tempNode.next = tailNode
  } else {
    tempNode = tailNode
    this.start = tailNode
  }

  this.length = this.length ? ++this.length : 1
};

MyLinkedList.prototype.addAtIndex = function (index, val) {
  if (index <= 0) return this.addAtHead(val)
  if (index === this.length) return this.addAtTail(val)
  if (index > this.length) return

  let addNode = new this.node(val)
  let cur = this.start

  while (index-- > 1) {
    cur = cur.next
  }
  addNode.next = cur.next
  cur.next = addNode
  this.length++
};

MyLinkedList.prototype.deleteAtIndex = function (index) {
  if (index < 0 || index >= this.length) return
  if (index) {
    let i = 1
    let cur = this.start
    while ((index - 1) >= i) {
      cur = cur.next
      i++
    }
    if (cur && cur.next) {
      cur.next = cur.next.next
    }
    this.length--

  } else {
    this.start = this.start.next
    this.length--
  }
};

3.反转链表

1.双指针法
关键：前指针进行交换和空变量

var reverseList = function(head) {
    if(!head || !head.next) return head  //空节点或者一个节点的时候只需返回头结点即可
    let pre = null, cur = head, temp = null
    // 排除空链表或者到尾结点的时候
    while(cur){
        // 翻转链表不是交换值，而是交换彼此的指针
        temp = cur.next
        cur.next = pre
        pre = cur
        cur = temp
    }
    return pre
};

2.递归法

var reverse = function (pre, head) {
    // 如果输入的这个尾结点为空,那么就结束条件，递归的结束条件
    if (!head) return pre
    let temp = head.next
    head.next = pre
    pre = head
    return reverse(pre, temp)
}
var reverseList = function (head) {
   return reverse(null,head)  //调用了某个函数记得一点要返回它的返回值
};

4.两两交换链表中的节点

//  三步
// 虚拟头指向 2 ；2 指向 1 ；1指向3
var swapPairs = function(head) {
    if(!head || !head.next) return head
    let ret = new ListNode(null,head)  // 将虚拟头结点指向head，这样方面后面做删除
   let cur = ret  //声明一个现在的节点指向头结点
    while(cur.next && cur.next.next){  //因为是两两交换所以要判断是否还有两个节点
        let temp = cur.next  //存储变量
        let temp2 = cur.next.next.next  //存储变量
        
        cur.next = cur.next.next //步骤一
        cur.next.next = temp  //步骤二
        cur.next.next.next = temp2 //步骤三

        cur = cur.next.next  //cur移动两位进行下一轮的交换
    }
    return ret.next //返回真正的头结点
};

5.删除链表的倒数第N个节点

双指针的经典应用，如果要删除倒数第n个节点，让fast移动n+1步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。

```javascript
//  这道题使用快慢指针 /快慢指针同时指向头结点，从而根据条件进行移动
var removeNthFromEnd = function(head, n) {
    // 创建虚拟头节点
    let res = new ListNode(null,head)
    let  fast= res
    let slow = res
    // 让快指针先向前移动n次
    while(n-- > 0 && fast.next){
        fast = fast.next
    }
    // 让快指针多移动一步
    fast = fast.next
    // 让快慢指针同时进行移动
    while(fast){
        fast = fast.next
        slow = slow.next
    }
    // 进行删除节点
    slow.next = slow.next.next
    return res.next
};

6.链表相交

1.求出两个链表的长度，并求出两个链表长度的差值，然后让curA移动到，和curB 末尾对齐的位置
2.就可以比较curA和curB是否相同，如果不相同，同时向后移动curA和curB，如果遇到curA == curB，则找到交点。

//交点不是数值相等，而是指针相等
var getLength = function (head) {
    let length = 0, cur = head
    while (cur) {
        cur = cur.next
        ++length
    }
    return length
}
var getIntersectionNode = function (headA, headB) {
    let curA = headA, curB = headB
    // 获取两个链表的长度
    let lengthA = getLength(headA)
    let lengthB = getLength(headB)

    // 保证链表的A是长链表,进行交换头结点以及长度
    if (lengthB > lengthA) {
        // js中的解构赋值
        // 下面交换变量注意加 “分号” ，两个数组交换变量在同一个作用域下时
        // 如果不加分号，下面两条代码等同于一条代码: [curA, curB] = [lenB, lenA]
        [lengthB, lengthA] = [lengthA, lengthB];
        [curA, curB] = [curB, curA];
    }
    let i = lengthA - lengthB
    // 获取差值后让长的链表先移动
    while (i-- > 0 && curA) {
        curA = curA.next
    }
    // 现在让他们同时移动，以及去对比是否有相同的值,循环条件为指针不为空，以及两个值不相等
    while (curA && curA != curB) {  //存在且相等
        curA = curA.next
        curB = curB.next
    }
    // 如果有相等的就跳出上面的循环，此时curA或者curB就是相交节点，如果循环结束后还是没有焦点，那么curA为空
    return curA
};

7.环形链表I

var hasCycle = function (head) {
    let fast = head, slow = head
    // 循环条件为快指针不为空，为空则不相交
    while (fast && fast.next) { //这里fast的话也就是判断空节点或者一个节点
         fast = fast.next.next
        slow = slow.next
        if (fast == slow) {
            return true
        }
    }
    return false
};

8.环形链表II

1.(x + y) * 2 = x + y + n (y + z)
2.当 n为1的时候，公式就化解为 x = z:从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点。
3.那么 n如果大于1是什么情况呢，就是fast指针在环形转n圈之后才遇到 slow指针。

var detectCycle = function(head) {
     let fast = head, slow = head
    // 循环条件为快指针不为空，为空则不相交
    while (fast && fast.next) { //这里fast的话也就是判断空节点或者一个节点
         fast = fast.next.next
        slow = slow.next
        if (fast == slow) {  //当快慢指针相遇的时候再命名两个指针同时倒退直至相遇就是入口的节点
        let index1 = head
        let index2 = fast
            while(index1 != index2){ 
                index1 = index1.next
                index2 = index2.next
            }
            return index1//返回环的入口
        }
    }

三、哈希表

• 哈希表：都是用来快速判断一个元素是否出现集合里。

• 对于哈希表，要知道哈希函数和哈希碰撞在哈希表中的作用.

• 哈希函数是把传入的key映射到符号表的索引上。

• 哈希碰撞处理有多个key映射到相同索引index上时的情景，处理碰撞的普遍方式是拉链法和线性探测法。

• 拉链法：发生冲突的元素都被存储在链表中

• 线性探测法：一定要保证tableSize大于dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题

• 哈希法也是牺牲了空间换取了时间，因为我们要使用额外的数组，set或者是map来存放数据，才能实现快速的查找。

1.有效的字母异位词

1.解法哈希表

var isAnagram = function(s, t) {
    // 使用数组当做哈希表，存放对应出现的次数，通过ASII码进行做对应
    let arr = new Array(26).fill(0)
    let x = "a".charCodeAt()
    // 循环遍历第一个字符串
    for(let i = 0 ; i < s.length ;i++){
        arr[s[i].charCodeAt() - x]++
    }
     for(let i = 0 ; i < t.length ;i++){
        arr[t[i].charCodeAt() - x]--
    }
    // 循环遍历数组中是否有不为0的元素
    for(let i = 0; i < arr.length;i++){
        if(arr[i] != 0) return false  // record数组如果有的元素不为零0，说明字符串s和t 一定是谁多了字符或者谁少了字符。
    }
    return true
};

2.解法
// t 是 ss 的异位词等价于「两个字符串排序后相等」。因此我们可以对字符串 ss 和 tt 分别排序，看排序后的字符串是否相等即可判断。此外，如果 ss 和 tt 的长度不同，tt 必然不是 ss 的异位词。

var isAnagram = function (s, t) {
    // 1.长度不同那么里面出现的字符和数量一定不同
    if (s.length != t.length) return false
    // 2.进行排序载进行对比 sort是数组的方法，先将字符串转换为数组
//   先是将字符串里面的数值列举出来，然后进行排序，再进行拼接成字符串再进行比较
    return [...s].sort().join('') === [...t].sort().join('')
};

1.1赎金信

//  1.短的字符串只能使用长字符串中的一次!
// 2.短的字符串由长字符串中的字母构成!
// 因为全都是英文字母组成26个小写，直接编写一个数组存放字母出现的次数
var canConstruct = function(ransomNote, magazine) {
    if(ransomNote.length > magazine.length) return false
    // 创建一个空数组存放出现字母出现的次数
    let arr = new Array(26).fill(0)
    // 1.先遍历长的字符串，统计每个字符串出现的次数
    for(let ch of magazine){
        arr[ch.charCodeAt() - 'a'.charCodeAt()]++
    }
    for(let ch of ransomNote){
        arr[ch.charCodeAt() - 'a'.charCodeAt()]--
        // 如果减到为负值说明M里面没有R里面的字母，或者字符数量不够多
        if(arr[ch.charCodeAt() -'a'.charCodeAt()] < 0){
            return false
        }
    }
    return true
};

1.2字母异位词分组

1.字符串的相同点为哈希表的键
2.具有相同点的键即存为哈希表的值
总结：遍历每个字符串，对于每个字符串，得到该字符串所在的一组字母异位词的标志，将当前字符串加入该组字母异位词的列表中。遍历全部字符串之后，哈希表中的每个键值对即为一组字母异位词。
分别使用排序和计数作为哈希表的键。

//  字母异位词指字母相同，但排列不同的字符串
// 方法一 计数
// 1.对象的键为计数 2.对象的键值为值  键和键值都是数组,键是数组就能计数，键值是数组就能存放相同计数的值
1.对象的键为计数 2.对象的键值为值  键和键值都是数组,键是数组就能计数，键值是数组就能存放相同计数的值
var groupAnagrams = function(strs) {  //str只是一个数组
    // 初始化一个空对象
    let map = new Object()
    for(let s of strs){
        // 初识化一个计数器 都是小写字母所以直接使用26个英文字母的数组进行计数
        let count = new Array(26).fill(0)
        for(let i of s){
            count[i.charCodeAt() - 'a'.charCodeAt()]++
        }
        // 进行对象里面的键值判断是否存在
        map[count] ? map[count].push(s) :map[count] = [s] //这里让键值等于一个数组，所以前面可以直接push
    }
    // 返回数组，对象转换为数组
    return Object.values(map)
};


// 方法二排序
var groupAnagrams = function(strs) {
    const map = new Map()
//   将排序之后的字符串作为哈希表的键
    for(let s of strs){
        let arr = Array.from(s)  //将字符串转换为数组，将每个数组进行排序
        arr.sort()
        // 将排序好的数组转换为字符串作为键值
        let key = arr.toString()
        // 开始没有key和arr或者s 就要取一个值进行判断
        let list = map.get(key) ? map.get(key) : []
         list.push(s)
        map.set(key,list)

    }
    return Array.from(map.values())
};

$1.3找到字符串中所有字母异位词（滑动窗口）

滑动窗口+哈希表
https://leetcode.cn/problems/find-all-anagrams-in-a-string/solution/hua-dong-chuang-kou-tong-yong-si-xiang-jie-jue-zi-/

2.两个数组的交集

用哈希表进行去重主要使用set
直接使用set 不仅占用空间比数组大，而且速度要比数组慢，set把数值映射到key上都要做hash计算的。
但是要注意，使用数组来做哈希的题目，是因为题目都限制了数值的大小。
而这道题目没有限制数值的大小，就无法使用数组来做哈希表了。
而且如果哈希值比较少、特别分散、跨度非常大，使用数组就造成空间的极大浪费。

var intersection = function(nums1, nums2) {
    // 初始化将长的数组元素放入哈希表中
    if(nums1.length < nums2.length){
        [nums1,nums2] = [nums2,nums1]
    }
    let set = new Set(nums1)  //无论是数组还是字符串都会将元素分开放进去
    let set1 = new Set()
    for(let ch of nums2){
        set.has(ch) && set1.add(ch)
    }
    return Array.from(set1)
};

扩展
与&&运算时 ，如果前面的都为true，就会继续向后执行，直到出现为false的结果或者到最后一个
或||运算，只要遇到真就返回那个真，不然就一直向后
set.add()会自动去重

3.两个数组的交集 II

不用哈希表，使用索引值去销毁

var intersect = function(nums1, nums2) {
    if(nums1.length < nums2.length){
        [nums1,nums2] = [nums2,nums1]
    }
    // let set = new Set(nums1)
    let arr = []
    for(let ch of nums2){
        let index = nums1.indexOf(ch)
        if(index !=-1){
            arr.push(ch)
            nums1[index] = null;
        }

    }
    return arr
};

4.快乐数

不是快乐数的话会无限循环，那么也就是说求和的过程中，sum会重复出现，重复出现后就返回false，快速判断一个元素是否出现集合里的时候，就要考虑哈希法

方法一，位数求和函数+根据条件使用哈希表进行判断是否重复+从而一直求和进行判断

// 方法一，位数求和函数+根据条件使用哈希表进行判断是否重复+从而一直求和进行判断
var isHappy = function (n) {
    // 初始化一个哈希表判断sum是否重复
    let set = new Map()
    // 创建一个取和函数
    let getsum = function (n) {
        let sum = 0
        while (n) {
            let d=  (n % 10)//初始化变量不能和+=一起使用
            sum += d*d
            n = Math.floor(n/10)
        }
        return sum
    }
    // 如果不符合这两个条件就一直进行求和，然后进行判断
   while(true){
     let sum =  getsum(n)   
    if(set.has(sum)) return false
    if(sum === 1) return true
    set.set(sum,1)
    // 一定记得更新n值从而继续进行求和
    n = sum
   }
   
}

// 方法二，快慢指针，慢指针是旧值，快指针是新值，新值和旧值相等时，或者快等于1时则退出返回对应

var isHappy = function (n) {
    let getNext = function (n) {
        let totalSum = 0;
        while (n > 0) {
            let d = n % 10;
            n =parseInt( n / 10);
            totalSum += d * d;
        }
        return totalSum;
    }
初始化快慢值
    let slow = n;
    let fast = getNext(n);
    while (fast !== 1 && fast !== slow) {
        slow = getNext(slow);
        fast = getNext(getNext(fast));
    }
    符合某一个条件后就退出，从而判断快指针对应的值
    // 返回判断是否为1，不是一则相等则不是快乐数
    return fast === 1;
};

5.两数之和

    // 1. 哈希表中存放数值，目标值依次遍历相减数组中的元素
    // 2.相减值查看哈希表中是否有这个元素，有则直接返回下标，无则加入当前值以及下标
var twoSum = function(nums, target) {
    let map = new Map()
    // 因为返回的是索引值，因此需要下标值，使用循环而不是迭代
    for(let i = 0; i < nums.length; i++){
        if(!map.has(target - nums[i])){
            map.set(nums[i],i)
        }else {
            let index = map.get(target-nums[i])
            return [index,i]
        }

    }
};

6.四数相加II

//  1.定义一个map存储两个数组的和作为key值，value值作为出现次数
// 2.遍历两个数组数组出现的各种情况，进行放置到哈希表中
// 3.定义一个计数器
// 4.遍历后面两个数组中的值是否为负数，符合条件计数器加上对应出现的次数，不符合加0
var fourSumCount = function(nums1, nums2, nums3, nums4) {
    let map = new Map()
    for(let ch1 of nums1){
        for(let ch2 of nums2){
            const sum = ch1 + ch2
         map.set(sum,(map.get(sum) || 0)+1)  
        }
    }
    // 声明一个计数器
    let count = 0
    for(let ch3 of nums3){
        for(let ch4 of nums4){
            const sum = ch3+ch4
        count += (map.get(0-sum)||0)
        }
    }
    return count
};

7.三数之和

//  思路1.两个数组和存入哈希表中记录坐标，遍历第三个数组进行取值符合则取三个的坐标值
// 但是无法考虑到去重的情况，因为要求是不重复的三元组，重复的数组直接跳过，因此使用双指针进行去重
// 思路2.将数组进行排序，双指针去重进行收缩
var threeSum = function (nums) {
    let newnums = nums.sort((a, b) => a - b)
    let arr = []
    //    排除特殊情况，如果排序后第一个值大于0则直接返回空
    if (newnums[0] > 0) return []
    //    初始化第一值，作为i值
    for (let i = 0; i < newnums.length; i++) {
        let l = i + 1, r = newnums.length - 1
        if (newnums[i] > 0) return arr
        // 去重1
        if (i > 0 && newnums[i] == newnums[i - 1]) continue
        // 开始循环收缩左右指针，循环条件为相等，相等后重新进行遍历
        while (l < r) {
            // 数值放在循环更新里面，不然怎么更新sum,进行判断啊

            let kl = newnums[l], kr = newnums[r], k = newnums[i]
            let sum = kl + kr + k
            // 如何和大于0，则右指针收缩
            if (sum > 0) {
                r--
                // 去重2 23去重不需要也没关系，因为不符合会一直收缩，符合后在符合那里也会一直收缩
                //  while (r >l && newnums[r] == newnums[r + 1]) r--
            } else if (sum < 0) {
                l++
                // 去重3
                //  while (r >l &&newnums[l] == newnums[l - 1]) l++
            } else {
                // 如果和相等的情况下，可以将下标值压入新的数组中
                arr.push([k, kl, kr])
                // 去重相等之后也要继续去重
                while (r > l && newnums[r] == newnums[r - 1]) r--
                while (r > l && newnums[l] == newnums[l + 1]) l++
                // 找到答案时双指针进行收缩
                l++
                r--
            }

        }
    }
    return arr
};

8.四数之和

//  和三数之和区别是将多一层循环暴力列举可能，然后拿双指针降一层循环
// 注意：1.target可能是负值，因此要进行判断过滤
// 2.多层循环进行叠加
var fourSum = function (nums, target) {
    let len = nums.length, arr = []
    // 数组的元素起码大于四位数字，否则无法对应
    if (len < 4) return []
    // 双指针必须要排排序排序
    nums.sort()
    // 第一层循环
    for (let i = 0; i < len - 3; i++) {
        // 去重
        if (i > 0 && nums[i] === nums[i - 1]) continue
        // 第二层循环
        for (let j = i + 1; j < len - 2; j++) {
            if (j > i + 1 && nums[j] === nums[j - 1]) continue
            // 内层双指针
            let l = j + 1, r = len - 1
            while (l < r) {
                let sum = nums[i] + nums[j] + nums[r] + nums[l]
                if (sum > target) {
                    r--
                    // while (r >l && nums[r] == nums[r + 1]) r--
                } else if (sum < target) {
                    l++
                    // while (r >l &&nums[l] == nums[l - 1]) l++
                } else {
                    arr.push([nums[i], nums[j], nums[l], nums[r]])
                    // 相等之后，还要继续进行移动，因此要继续去重
                    while (l < r && nums[l] === nums[l + 1]) l++
                    while (l < r && nums[r] === nums[r - 1]) r--
                    // 找到答案时开始同时收缩
                l++
                r--
                }

            }
        }
    }
    return arr
};

四、字符串

1.反转字符串

对于字符串，我们定义两个指针（也可以说是索引下标），一个从字符串前面，一个从字符串后面，两个指针同时向中间移动，并交换元素。
因为字符串也是一种数组，所以元素在内存中是连续分布，这就决定了反转链表和反转字符串方式上还是有所差异的。

var reverseString = function (s) {
    let n = s.length
    let left = 0, right = n - 1
    while (left < right) {
        // 交换三步骤可以简写  [s[left], s[right]] = [s[right], s[left]];
        let temp = s[right]
        s[right] = s[left]
        s[left] = temp
        left++
        right--
    }
};

2.反转字符串II

所以当需要固定规律一段一段去处理字符串的时候，要想想在在for循环的表达式上做做文章。

//  1.2k个进行翻转，for循环中进行操作
// 2.细节是小于2k,大于k,或者小于k个的翻转
var reverseStr = function(s, k) {
    // 先将字符串转换为数组然后可以操作交换
    let arr = s.split("")
    for(let i = 0;  i < s.length ; i += 2*k){
        let l = i-1//这里减一是为了与右边进行同步
        // 右边界进行判断处理
        let r = i + k > arr.length ? arr.length : i + k
        // 初识值l在外，r也在外，因此要在进行数据交换之前进行加减
        while(++l < --r){  //先进行向内缩进再进行交换
            [arr[l],arr[r]] = [arr[r],arr[l]]
            
           
        }
    }
    return arr.join("")
};

3.替换空格

var replaceSpace = function (s) {
    // 先统计空格数，然后延长数组，使用双指针进行交换
    let count = 0
    // 字符串的操作先将数组转化为数组
    let arr = s.split("")
    for (let i = 0; i < arr.length; i++) {
        if (arr[i] === ' ') {
            count++
        }
    }
    //创建左右指针
    let l = arr.length - 1
    let r = arr.length + count * 2 - 1
    // 进行指针的移动以及判断进行交换
    // 循环结束的条件为左指针移动到头
    while (l >= 0) {
        if (arr[l] === ' ') {
            arr[r--] = "0"
            arr[r--] = "2"
            arr[r--] = "%"
            l--
        } else {
            [arr[r],arr[l]] = [arr[l],arr[r]]
            l--
            r--
        }

    }
    return arr.join("")
};

$4.翻转字符串里的单词

5.左旋转字符串

//  局部翻转+整体翻转
// 1.翻转前n
// 2.翻转后面
// 3.翻转整个
var reverseLeftWords = function (s, n) {
    // 因为JS内部的reverse方法不能指定翻转位置，自己封装函数
    let reverse = function (arr, start, end) {
        while (start < end) {
            [arr[start], arr[end]] = [arr[end], arr[start]]
            start++
            end--
        }
        return arr
    }
    // 转换字符串为数组
    let arr = Array.from(s)
    let len = arr.length
    // reverse(arr, 0, len-1)
    // reverse(arr, 0, len -n- 1)
    // reverse(arr, len-n, len-1)
    reverse(arr, 0, n-1)
    reverse(arr, n, len-1)
    reverse(arr, 0, len-1)
    return arr.join("")
};

# 6.实现 strStr() KMP

扩展：
KMP算法是一种改进的字符串匹配算法，KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n) [1] 。

匹配过程：最长相符前后缀(将前缀表进行记录，冲突后，找到前缀表前一位所对应的值与其相等的前缀后面的一个位置继续匹配) 位置其实就是最长相等前后缀的长度

前缀：包含首字母，不包含尾字母的就是前缀
前缀表：记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

next数组：用来回退到下一个地址

#最长公共前后缀？

#7.重复的子字符串 KMP

五、双指针法

六、栈和队列

队列是先进先出，栈是先进后出
栈提供push 和 pop 等等接口，所有元素必须符合先进后出规则，所以栈不提供走访功能，也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素

1.用栈实现队列

使用栈来模式队列的行为，如果仅仅用一个栈，是一定不行的，所以需要两个栈一个输入栈，一个输出栈，这里要注意输入栈和输出栈的关系
思路：

• 在push数据的时候，只要数据放进输入栈就好，
• 但在pop的时候，操作就复杂一些，输出栈如果为空，就把进栈数据全部导入进来（注意是全部导入）
• 再从出栈弹出数据，如果输出栈不为空，则直接从出栈弹出数据就可以

      // 使用两个数组的栈方法（push, pop） 实现队列
    //   push(x) -- 将一个元素放入队列的尾部。
// pop() -- 从队列首部移除元素。
// peek() -- 返回队列首部的元素。
// empty() -- 返回队列是否为空。
// 利用数组的pop push方法模拟栈封装一个队列
         function myQueue() {
            this.stackIn = []
            this.stackOut = []
        }
        // 给构造函数的原型上封装队列的push方法
        myQueue.prototype.push = function(x){
            this.stackIn.push(x)
        }
        // pop方法  队列的输出是先进先出,两个栈模拟先进先出：
        // 输出栈如果为空，就把进栈数据全部导入进来（注意是全部导入）
        //  再从出栈弹出数据，如果输出栈不为空，则直接从出栈弹出数据就可以
        myQueue.prototype.pop = function(){
            let length = this.stackOut.length
            if(length) { //输出栈不为空则依次先将输出栈中的元素推出
             return   this.stackOut.pop() 
            }
            // 输出栈如果为空，就把进栈数据全部导入进来（注意是全部导入）
            while(this.stackIn.length){
                this.stackOut.push(this.stackIn.pop())
            }
            // 全部导入后再出栈
            return this.stackOut.pop()
        }
        // 获取头部数据
        myQueue.prototype.peek = function(){
            // 先将绑定的数据栈中最后一位导出，再推进去就是头部数据
            const x = this.pop()
            this.stackOut.push(x)
            return x;
        }

        // 
        myQueue.prototype.empy = function(){
            return !this.stackIn.length && !this.stackOut.length
        }

2.用队列实现栈

var MyStack = function () {  //push尾 shift头   栈：push尾 pop尾
    this.queue = []
};

/** 
 * @param {number} x
 * @return {void}
 */
MyStack.prototype.push = function (x) {
    return this.queue.push(x)
};

/**
 * @return {number}
 */
MyStack.prototype.pop = function () {
    let size = this.queue.length
    while (size > 1) {
        this.queue.push(this.queue.shift())  //这个循环的目的就是将头元素后面的元素都放到自己的后面
        --size //先减减
    }
    return this.queue.shift()
};

/**
 * @return {number}
 */
MyStack.prototype.top = function () {
    let x = this.pop()
    this.queue.push(x)
    return x
};

/**
 * @return {boolean}
 */
MyStack.prototype.empty = function () {
    return !this.queue.length
};

3.有效的括号

在匹配左括号的时候，右括号先入栈，就只需要比较当前元素和栈顶相不相等就可以
三种情况：1.2.3.

//  只包括 '('，')'，'{'，'}'，'['，']' 的字符串
var isValid = function (s) {
    let stack = [] //创建一个栈，将没有左符号放入
   let map = {
       "{":"}",
       "(":")",
       "[":"]"
   }
   for(let c of s){
    //  如果是左括号是入栈
       if(c in map){
           stack.push(c)  //这一步获取整个字符串的左括号，将左括号压入栈中
           continue //符合就继续循环判断
       }
    //    如果不是左括号就是右括号，就开始对比栈中元素是否一一对应
    //   将字符串中的左括号入栈之后，，开始比较栈顶的元素依次比较,并且依次弹出
    if(c !== map[stack.pop()]){  //根据左括号去寻找对应的右括号
        return false //有一个不相同则返回错  //第一种右侧多了情况，相等不相同的情况
    }
   
   }   
     return !stack.length //相等相同的情况，左侧多了的情况
};

4.删除字符串中的所有相邻重复项

• **在企业项目开发中，尽量不要使用递归！**在项目比较大的时候，由于参数多，全局变量等等，使用递归很容易判断不充分return的条件，非常容易无限递归（或者递归层级过深），造成栈溢出错误
• 从栈中弹出剩余元素，此时是字符串ac，因为从栈里弹出的元素是倒序的，所以在对字符串进行反转一下,但是本题是使用数组模拟栈，不用依次推出来，直接转换为字符串

var removeDuplicates = function(s) {
    // 栈进栈和栈顶里面的元素进行对比，依次进行对比 压栈进栈
    let stock = []
    for(const ch of s){
        if(stock.length && stock[stock.length-1] == ch){
            stock.pop(ch)
        }else {
            stock.push(ch)
        }
    }
    // 将数组连接成字符串
    return stock.join('')
};

5.逆波兰表达式求值

//  逆波兰式的优势：
//  去掉括号也行正常运行
//  适合用栈操作运算：遇到数字则入栈；遇到运算符则取出栈顶两个数字进行计算，并将结果压入栈中
// 其实逆波兰表达式相当于是二叉树中的后序遍历。 大家可以把运算符作为中间节点，按照后序遍历的规则画出一个二叉树。
var evalRPN = function(tokens) {
    let stock = []
    for(let ch of tokens){
        if(ch == "+" || ch == "-" || ch == "*" || ch == "/"){
            let num1 = parseInt(stock.pop())
            let num2 = parseInt(stock.pop() ) //这个才是上一次的表达式结果
            if(ch == '+'){stock.push(num2+num1)}
            if(ch == '-'){stock.push(num2-num1)}
            if(ch == '*'){stock.push(num2*num1)}
            if(ch == '/'){stock.push(parseInt(num2/num1))}
        }else {
            stock.push(ch)
        }
    }
    // 返回栈中的结果
     return stock.pop()
};

￥6.滑动窗口最大值

单调队列，即单调递减或单调递增的队列，和优先级队列不同，只需维护最大的那个数字将大小进行替换。

7.前 K 个高频元素

优先级队列：其实就是一个披着队列外衣的堆，因为优先级队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列。
堆：堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。

8.简化路径

七、二叉树

八、回溯算法

九、贪心算法（不要忽视）

十、动态规划

十一、排序算法

摘要：
冒泡：依次比较两个相邻元素，前一个元素比后一个元素大，就交换，最大元素在末尾。
选择：从序列中选择最小的元素存放在新序列的起始位置，再从剩余的元素中继续寻找最小元素，存放到新序列末尾，依次执行，直到排序完成
插入：第一个元素看做有序序列，从第二个元素开始，插入有序序列，当前元素与前面已经排好序的元素比较，小于就交换。
归并希尔：采用二分法，将序列一直不断的分组，直到小于2个元素，分组排序后再合并。
快速：找一个基准，剩余元素与基准进行对比，小于放入left，大于放入right，递归调用。