【Numpy】
目录
常数
#判断array中是否有几个空值
数据类型
时间日期和时间增量
给定一系列不连续的日期序列。填充缺失的日期,使其成为连续的日期序列。
如何得到昨天,今天,明天的的日期
数组
array
如何在给定起始点、长度和步骤的情况下创建一个numpy数组序列
如何将图像转换为numpy数组
asarray
fromfunction
固定数组
创建一个二维数组,其中边界值为1,其余值为0
利用数值范围来创建ndarray
结构数组
数组的属性
副本与视图
索引与切片
整数索引
#利用负数下标翻转数组
切片索引
dots 索引
整数数组索引
numpy.take
使用切片索引到numpy数组时,生成的数组视图将始终是原始数组的子数组, 但是整数数组索引,不是其子数组,是形成新的数组。
布尔索引
去除数组中的空值
数组迭代
应用
数组操作
更改形状
numpy.ndarray.shape
numpy.ndarray.flat
numpy.ndarray.flatten([order='C'])
umpy.ravel(a, order='C')
numpy.reshape(a, newshape[, order='C'])
数组转置
numpy.transpose(a, axes=None)
numpy.ndarray.T
更改维度
numpy.newaxis
numpy.squeeze(a, axis=None)
数组组合
numpy.concatenate((a1, a2, ...), axis=0, out=None)
numpy.stack(arrays, axis=0, out=None)
numpy.vstack(tup)
numpy.hstack(tup)
数组拆分
numpy.split(ary, indices_or_sections, axis=0)
numpy.vsplit(ary, indices_or_sections)
numpy.hsplit(ary, indices_or_sections)
数组平铺
numpy.tile(A, reps)
numpy.repeat(a, repeats, axis=None)
添加和删除元素
np.unique
应用
#将 arr的2维数组按列输出。
给定两个随机数组A和B,验证它们是否相等。
在给定的numpy数组中找到重复的条目(第二次出现以后),并将它们标记为True。第一次出现应为False。
函数
np.diff
np.hstack
np.logical_not
np.mean
numpy是python中基于数组对象的科学计算库。
拥有n维数组对象; 拥有广播功能(后面讲到); 拥有各种科学计算API
n维数组(ndarray)对象,是一系列同类数据的集合,可以进行索引、切片、迭代操作。
常数
#nan = NaN = NAN 表示空值
import numpy as np
#两个np.nan 不相等
print(np.nan == np.nan)
print(np.nan != np.nan)
#用于统计数组中非零元素的个数
z = np.count_nonzero(x)
print(z)
#np.inf 正无穷大
Inf = inf = infty = Infinity = PINF
#np.pi 圆周率
#np.e#判断array中是否有几个空值
x = np.array([1, 1, 6, np.NAN, 3])
print(x)
y = np.isnan(x)
print(y)
z = np.count_nonzero(y)
print(z) 空值计算结果还是空值
空值和空值比较是False np.isnan(x)
浮点数比较 isclose()
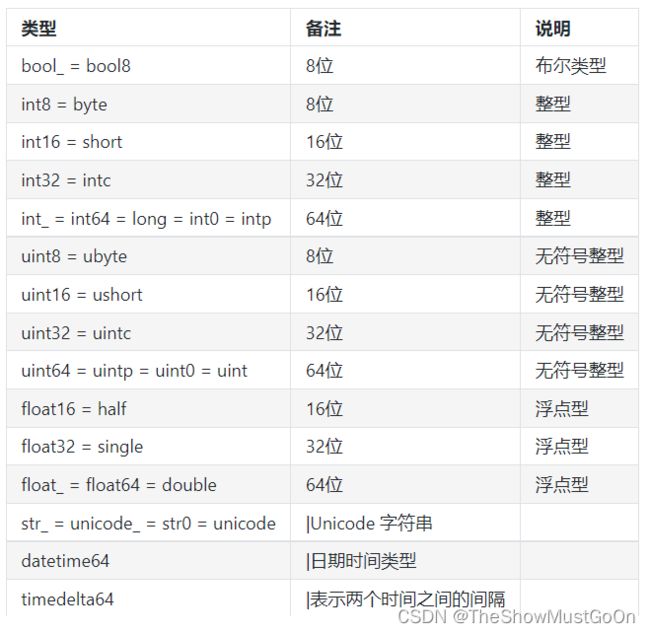
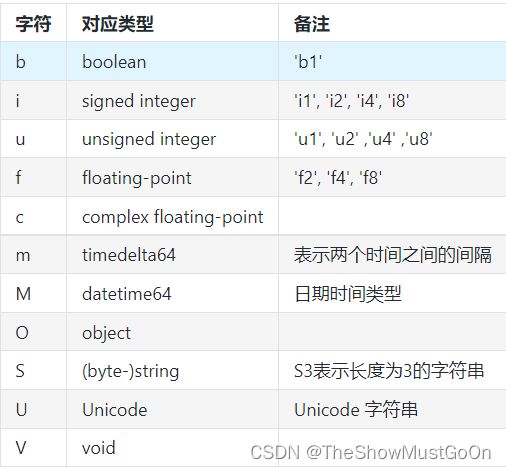
数据类型
dtype=np.bool_
numpy 的数值类型实际上是 dtype 对象的实例。
class dtype(object):
def __init__(self, obj, align=False, copy=False):
pass#itemsize输出array元素的字节数
a = np.dtype('b1')
print(a.type) #
print(a.itemsize) # 1
a = np.dtype('i1')
print(a.type) #
print(a.itemsize) # 1
a = np.dtype('i2')
print(a.type) #
print(a.itemsize) # 2
a = np.dtype('i4')
print(a.type) #
print(a.itemsize) # 4
a = np.dtype('i8')
print(a.type) #
print(a.itemsize) # 8
a = np.dtype('u1')
print(a.type) #
print(a.itemsize) # 1
a = np.dtype('u2')
print(a.type) #
print(a.itemsize) # 2
a = np.dtype('u4')
print(a.type) #
print(a.itemsize) # 4
a = np.dtype('u8')
print(a.type) #
print(a.itemsize) # 8
a = np.dtype('f2')
print(a.type) #
print(a.itemsize) # 2
a = np.dtype('f4')
print(a.type) #
print(a.itemsize) # 4
a = np.dtype('f8')
print(a.type) #
print(a.itemsize) # 8
a = np.dtype('S')
print(a.type) #
print(a.itemsize) # 0
a = np.dtype('S3')
print(a.type) #
print(a.itemsize) # 3
a = np.dtype('U3')
print(a.type) #
print(a.itemsize) # 12 #numpy.iinfo()函数显示整数类型的机器限制
ii16 = np.iinfo(np.int16)
print(ii16.min) # -32768
print(ii16.max) # 32767
ii32 = np.iinfo(np.int32)
print(ii32.min) # -2147483648
print(ii32.max) # 2147483647
#numpy.finfo()函数显示浮点类型的机器限制。
ff16 = np.finfo(np.float16)
print(ff16.bits) # 16
print(ff16.min) # -65500.0
print(ff16.max) # 65500.0
print(ff16.eps) # 0.000977
ff32 = np.finfo(np.float32)
print(ff32.bits) # 32
print(ff32.min) # -3.4028235e+38
print(ff32.max) # 3.4028235e+38
print(ff32.eps) # 1.1920929e-07时间日期和时间增量
#从字符串创建 datetime64 类型时,默认情况下,numpy 会根据字符串自动选择对应的单位。
a = np.datetime64('2020-03-01')
print(a, a.dtype) # 2020-03-01 datetime64[D]
a = np.datetime64('2020-03')
print(a, a.dtype) # 2020-03 datetime64[M]
a = np.datetime64('2020-03-08 20:00:05')
print(a, a.dtype) # 2020-03-08T20:00:05 datetime64[s]
a = np.datetime64('2020-03-08 20:00')
print(a, a.dtype) # 2020-03-08T20:00 datetime64[m]
a = np.datetime64('2020-03-08 20')
print(a, a.dtype) # 2020-03-08T20 datetime64[h]
#字符串创建 datetime64 类型时,可以强制指定使用的单位。
a = np.datetime64('2020-03', 'D')
print(a, a.dtype) # 2020-03-01 datetime64[D]
a = np.datetime64('2020-03', 'Y')
print(a, a.dtype) # 2020 datetime64[Y]
print(np.datetime64('2020-03') == np.datetime64('2020-03-01')) # True
print(np.datetime64('2020-03') == np.datetime64('2020-03-02')) #False
#从字符串创建 datetime64 数组时,如果单位不统一,则一律转化成其中最小的单位。
a = np.array(['2020-03', '2020-03-08', '2020-03-08 20:00'], dtype='datetime64')
print(a, a.dtype)
# ['2020-03-01T00:00' '2020-03-08T00:00' '2020-03-08T20:00'] datetime64[m]
#使用arange()创建 datetime64 数组,用于生成日期范围。
a = np.arange('2020-08-01', '2020-08-10', dtype=np.datetime64)
print(a)
# ['2020-08-01' '2020-08-02' '2020-08-03' '2020-08-04' '2020-08-05'
# '2020-08-06' '2020-08-07' '2020-08-08' '2020-08-09']
print(a.dtype) # datetime64[D]
a = np.arange('2020-08-01 20:00', '2020-08-10', dtype=np.datetime64)
print(a)
# ['2020-08-01T20:00' '2020-08-01T20:01' '2020-08-01T20:02' ...
# '2020-08-09T23:57' '2020-08-09T23:58' '2020-08-09T23:59']
print(a.dtype) # datetime64[m]
a = np.arange('2020-05', '2020-12', dtype=np.datetime64)
print(a)
# ['2020-05' '2020-06' '2020-07' '2020-08' '2020-09' '2020-10' '2020-11']
print(a.dtype) # datetime64[M]
#timedelta64 表示两个 datetime64 之间的差。timedelta64 也是带单位的,并且和相减运算中的两个 datetime64 中的较小的单位保持一致。
a = np.datetime64('2020-03-08') - np.datetime64('2020-03-07')
b = np.datetime64('2020-03-08') - np.datetime64('202-03-07 08:00')
c = np.datetime64('2020-03-08') - np.datetime64('2020-03-07 23:00', 'D')
print(a, a.dtype) # 1 days timedelta64[D]
print(b, b.dtype) # 956178240 minutes timedelta64[m]
print(c, c.dtype) # 1 days timedelta64[D]
a = np.datetime64('2020-03') + np.timedelta64(20, 'D')
b = np.datetime64('2020-06-15 00:00') + np.timedelta64(12, 'h')
print(a, a.dtype) # 2020-03-21 datetime64[D]
print(b, b.dtype) # 2020-06-15T12:00 datetime64[m]
# 生成 timedelta64时,要注意年('Y')和月('M')这两个单位无法和其它单位进行运算(一年有几天?一个月有几个小时?这些都是不确定的)。
a = np.timedelta64(1, 'Y')
b = np.timedelta64(a, 'M')
print(a) # 1 years
print(b) # 12 months
c = np.timedelta64(1, 'h')
d = np.timedelta64(c, 'm')
print(c) # 1 hours
print(d) # 60 minutes
print(np.timedelta64(a, 'D'))
# TypeError: Cannot cast NumPy timedelta64 scalar from metadata [Y] to [D] according to the rule 'same_kind'
print(np.timedelta64(b, 'D'))
# TypeError: Cannot cast NumPy timedelta64 scalar from metadata [M] to [D] according to the rule 'same_kind'
#timedelta64 的运算
a = np.timedelta64(1, 'Y')
b = np.timedelta64(6, 'M')
c = np.timedelta64(1, 'W')
d = np.timedelta64(1, 'D')
e = np.timedelta64(10, 'D')
print(a) # 1 years
print(b) # 6 months
print(a + b) # 18 months
print(a - b) # 6 months
print(2 * a) # 2 years
print(a / b) # 2.0
print(c / d) # 7.0
print(c % e) # 7 days
# numpy.datetime64 与 datetime.datetime 相互转换
import numpy as np
import datetime
dt = datetime.datetime(year=2020, month=6, day=1, hour=20, minute=5, second=30)
dt64 = np.datetime64(dt, 's')
print(dt64, dt64.dtype)
# 2020-06-01T20:05:30 datetime64[s]
dt2 = dt64.astype(datetime.datetime)
print(dt2, type(dt2))
# 2020-06-01 20:05:30
#将指定的偏移量应用于工作日,单位天('D')。计算下一个工作日,如果当前日期为非工作日,默认报错。可以指定 forward 或 backward 规则来避免报错。(一个是向前取第一个有效的工作日,一个是向后取第一个有效的工作日)
#offsets 为偏移量
# 2020-07-10 星期五
a = np.busday_offset('2020-07-10', offsets=1)
print(a) # 2020-07-13
a = np.busday_offset('2020-07-11', offsets=1)
print(a)
# ValueError: Non-business day date in busday_offset
a = np.busday_offset('2020-07-11', offsets=0, roll='forward')
b = np.busday_offset('2020-07-11', offsets=0, roll='backward')
print(a) # 2020-07-13
print(b) # 2020-07-10
a = np.busday_offset('2020-07-11', offsets=1, roll='forward')
b = np.busday_offset('2020-07-11', offsets=1, roll='backward')
print(a) # 2020-07-14
print(b) # 2020-07-13
# 返回指定日期是否是工作日。
# 2020-07-10 星期五
a = np.is_busday('2020-07-10')
b = np.is_busday('2020-07-11')
print(a) # True
print(b) # False
# 统计一个 datetime64[D] 数组中的工作日天数
begindates = np.datetime64('2020-07-10')
enddates = np.datetime64('2020-07-20')
a = np.arange(begindates, enddates, dtype='datetime64')
b = np.count_nonzero(np.is_busday(a)) #用来测试 有个True
print(a)
# ['2020-07-10' '2020-07-11' '2020-07-12' '2020-07-13' '2020-07-14'
# '2020-07-15' '2020-07-16' '2020-07-17' '2020-07-18' '2020-07-19']
print(b) # 6
#自定义周掩码值,即指定一周中哪些星期是工作日。
# 掩码是一串二进制代码对目标字段进行位与运算,屏蔽当前的输入位。
# 2020-07-10 星期五
a = np.is_busday('2020-07-10', weekmask=[1, 1, 1, 1, 1, 0, 0])
b = np.is_busday('2020-07-10', weekmask=[1, 1, 1, 1, 0, 0, 1])
print(a) # True
print(b) # False
# 返回两个日期之间的工作日数量。
# numpy.busday_count(begindates, enddates, weekmask='1111100', holidays=[], busdaycal=None, out=None)
# Counts the number of valid days between begindates and enddates, not including the day of enddates.
# 2020-07-10 星期五
begindates = np.datetime64('2020-07-10')
enddates = np.datetime64('2020-07-20')
a = np.busday_count(begindates, enddates)
b = np.busday_count(enddates, begindates)
print(a) # 6
print(b) # -6 给定一系列不连续的日期序列。填充缺失的日期,使其成为连续的日期序列。
import numpy as np
#给定
dates = np.arange('2020-02-01', '2020-02-10', 2, np.datetime64)
print(dates)
# ['2020-02-01' '2020-02-03' '2020-02-05' '2020-02-07' '2020-02-09']
print(np.diff(dates))
# [2 2 2 2]
for item in zip(dates, np.diff(dates)):
print(item)
# (numpy.datetime64('2020-02-01'), numpy.timedelta64(2,'D'))
# (numpy.datetime64('2020-02-03'), numpy.timedelta64(2,'D'))
# (numpy.datetime64('2020-02-05'), numpy.timedelta64(2,'D'))
# (numpy.datetime64('2020-02-07'), numpy.timedelta64(2,'D'))
out = []
for date, d in zip(dates, np.diff(dates)):
out.extend(np.arange(date, date + d))
fillin = np.array(out)
print(fillin)
# ['2020-02-01' '2020-02-02' '2020-02-03' '2020-02-04' '2020-02-05'
# '2020-02-06' '2020-02-07' '2020-02-08']
output = np.hstack([fillin, dates[-1]])
print(output)
# ['2020-02-01' '2020-02-02' '2020-02-03' '2020-02-04' '2020-02-05'
# '2020-02-06' '2020-02-07' '2020-02-08' '2020-02-09']如何得到昨天,今天,明天的的日期
import numpy as np
yesterday = np.datetime64('today', 'D') - np.timedelta64(1, 'D')
print(yesterday)数组
array
# numpy 提供的最重要的数据结构是ndarray,它是 python 中list的扩展。
# def array(p_object, dtype=None, copy=True, order='K', subok=False, ndmin=0):
# 创建一维数组
a = np.array([0, 1, 2, 3, 4])
b = np.array((0, 1, 2, 3, 4))
print(a, type(a))
# [0 1 2 3 4]
print(b, type(b))
# [0 1 2 3 4]
# 创建二维数组
c = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
print(c, type(c))
# [[11 12 13 14 15]
# [16 17 18 19 20]
# [21 22 23 24 25]
# [26 27 28 29 30]
# [31 32 33 34 35]]
# 创建三维数组
d = np.array([[(1.5, 2, 3), (4, 5, 6)],
[(3, 2, 1), (4, 5, 6)]])
print(d, type(d))
# [[[1.5 2. 3. ]
# [4. 5. 6. ]]
#
# [[3. 2. 1. ]
# [4. 5. 6. ]]] 如何在给定起始点、长度和步骤的情况下创建一个numpy数组序列
start
step
length
arr = np.arrange(start, start + step * length, step)如何将图像转换为numpy数组
img1 = Image.open('img1.jpg')
a = np.arrage(img1)
print(a.shape, a.dtype)asarray
# array()和asarray()都可以将结构数据转化为 ndarray,但是array()和asarray()主要区别就是当数据源是ndarray 时,array()仍然会 copy 出一个副本,占用新的内存,但不改变 dtype 时 asarray()不会。
x = [[1, 1, 1], [1, 1, 1], [1, 1, 1]]
y = np.array(x)
z = np.asarray(x)
x[1][2] = 2
print(x,type(x))
# [[1, 1, 1], [1, 1, 2], [1, 1, 1]]
print(y,type(y))
# [[1 1 1]
# [1 1 1]
# [1 1 1]]
print(z,type(z))
# [[1 1 1]
# [1 1 1]
# [1 1 1]]
x = np.array([[1, 1, 1], [1, 1, 1], [1, 1, 1]])
y = np.array(x)
z = np.asarray(x)
w = np.asarray(x, dtype=np.int)
x[1][2] = 2
print(x,type(x),x.dtype)
# [[1 1 1]
# [1 1 2]
# [1 1 1]] int32
print(y,type(y),y.dtype)
# [[1 1 1]
# [1 1 1]
# [1 1 1]] int32
print(z,type(z),z.dtype)
# [[1 1 1]
# [1 1 2]
# [1 1 1]] int32
print(w,type(w),w.dtype)
# [[1 1 1]
# [1 1 2]
# [1 1 1]] int32
# 更改为较大的dtype时,其大小必须是array的最后一个axis的总大小(以字节为单位)的除数
x = np.array([[1, 1, 1], [1, 1, 1], [1, 1, 1]])
print(x, x.dtype)
# [[1 1 1]
# [1 1 1]
# [1 1 1]] int32
x.dtype = np.float
# ValueError: When changing to a larger dtype, its size must be a divisor of the total size in bytes of the last axis of the array. fromfunction
# def fromfunction(function, shape, **kwargs):
# 通过在每个坐标上执行一个函数来构造数组。
def f(x, y):
return 10 * x + y
x = np.fromfunction(f, (5, 4), dtype=int)
print(x)
# [[ 0 1 2 3]
# [10 11 12 13]
# [20 21 22 23]
# [30 31 32 33]
# [40 41 42 43]]
x = np.fromfunction(lambda i, j: i == j, (3, 3), dtype=int)
print(x)
# [[ True False False]
# [False True False]
# [False False True]]
x = np.fromfunction(lambda i, j: i + j, (3, 3), dtype=int)
print(x)
# [[0 1 2]
# [1 2 3]
# [2 3 4]]固定数组
#零数组
# zeros()函数:返回给定形状和类型的零数组。
# zeros_like()函数:返回与给定数组形状和类型相同的零数组。
# def zeros(shape, dtype=None, order='C'):
# def zeros_like(a, dtype=None, order='K', subok=True, shape=None):
x = np.zeros(5)
print(x) # [0. 0. 0. 0. 0.]
x = np.zeros([2, 3])
print(x)
# [[0. 0. 0.]
# [0. 0. 0.]]
x = np.array([[1, 2, 3], [4, 5, 6]])
y = np.zeros_like(x)
print(y)
# [[0 0 0]
# [0 0 0]]
# ones()函数:返回给定形状和类型的1数组。
# ones_like()函数:返回与给定数组形状和类型相同的1数组。
# empty()函数:返回一个空数组,数组元素为随机数。
# empty_like函数:返回与给定数组具有相同形状和类型的新数组。
# eye()函数:返回一个对角线上为1,其它地方为零的单位数组。
# identity()函数:返回一个方的单位数组。
x = np.eye(4)
print(x)
# [[1. 0. 0. 0.]
# [0. 1. 0. 0.]
# [0. 0. 1. 0.]
# [0. 0. 0. 1.]]
x = np.eye(2, 3)
print(x)
# [[1. 0. 0.]
# [0. 1. 0.]]
x = np.identity(4)
print(x)
# [[1. 0. 0. 0.]
# [0. 1. 0. 0.]
# [0. 0. 1. 0.]
# [0. 0. 0. 1.]]
#full()函数:返回一个常数数组。
#full_like()函数:返回与给定数组具有相同形状和类型的常数数组。
def full(shape, fill_value, dtype=None, order='C'):
def full_like(a, fill_value, dtype=None, order='K', subok=True, shape=None):
x = np.full((2,), 7)
print(x)
# [7 7]
x = np.full(2, 7)
print(x)
# [7 7]
x = np.full((2, 7), 7)
print(x)
# [[7 7 7 7 7 7 7]
# [7 7 7 7 7 7 7]]
x = np.array([[1, 2, 3], [4, 5, 6]])
y = np.full_like(x, 7)
print(y)
# [[7 7 7]
# [7 7 7]]
创建一个二维数组,其中边界值为1,其余值为0
Z = np.ones((10, 10))
Z[1:-1, 1:-1] = 0
利用数值范围来创建ndarray
arange()函数:返回给定间隔内的均匀间隔的值。linspace()函数:返回指定间隔内的等间隔数字。logspace()函数:返回数以对数刻度均匀分布。numpy.random.rand()返回一个由[0,1)内的随机数组成的数组。
def arange([start,] stop[, step,], dtype=None):
def linspace(start, stop, num=50, endpoint=True, retstep=False,
dtype=None, axis=0):
def logspace(start, stop, num=50, endpoint=True, base=10.0,
dtype=None, axis=0):
def rand(d0, d1, ..., dn): x = np.arange(5)
print(x) # [0 1 2 3 4]
x = np.arange(3, 7, 2)
print(x) # [3 5]
x = np.linspace(start=0, stop=2, num=9)
print(x)
# [0. 0.25 0.5 0.75 1. 1.25 1.5 1.75 2. ]
x = np.logspace(0, 1, 5)
print(np.around(x, 2))
# [ 1. 1.78 3.16 5.62 10. ]
#np.around 返回四舍五入后的值,可指定精度。
# around(a, decimals=0, out=None)
# a 输入数组
# decimals 要舍入的小数位数。 默认值为0。 如果为负,整数将四舍五入到小数点左侧的位置
x = np.linspace(start=0, stop=1, num=5)
x = [10 ** i for i in x]
print(np.around(x, 2))
# [ 1. 1.78 3.16 5.62 10. ]
x = np.random.random(5)
print(x)
# [0.41768753 0.16315577 0.80167915 0.99690199 0.11812291]
x = np.random.random([2, 3])
print(x)
# [[0.41151858 0.93785153 0.57031309]
# [0.13482333 0.20583516 0.45429181]]结构数组
#首先需要定义结构,然后利用np.array()来创建数组,其参数dtype为定义的结构
#字典
personType = np.dtype({
'names': ['name', 'age', 'weight'],
'formats': ['U30', 'i8', 'f8']})
a = np.array([('Liming', 24, 63.9), ('Mike', 15, 67.), ('Jan', 34, 45.8)],
dtype=personType)
print(a, type(a))
# [('Liming', 24, 63.9) ('Mike', 15, 67. ) ('Jan', 34, 45.8)]
#
#包含多个元组的列表
personType = np.dtype([('name', 'U30'), ('age', 'i8'), ('weight', 'f8')])
a = np.array([('Liming', 24, 63.9), ('Mike', 15, 67.), ('Jan', 34, 45.8)],
dtype=personType)
print(a, type(a))
# [('Liming', 24, 63.9) ('Mike', 15, 67. ) ('Jan', 34, 45.8)]
#
# 结构数组的取值方式和一般数组差不多,可以通过下标取得元素:
print(a[0])
# ('Liming', 24, 63.9)
print(a[-2:])
# [('Mike', 15, 67. ) ('Jan', 34, 45.8)]
# 我们可以使用字段名作为下标获取对应的值
print(a['name'])
# ['Liming' 'Mike' 'Jan']
print(a['age'])
# [24 15 34]
print(a['weight'])
# [63.9 67. 45.8] 数组的属性
#在使用 numpy 时,你会想知道数组的某些信息。很幸运,在这个包里边包含了很多便捷的方法,可以给你想要的信息。
#numpy.ndarray.ndim用于返回数组的维数(轴的个数)也称为秩,一维数组的秩为 1,二维数组的秩为 2,以此类推。
#numpy.ndarray.shape表示数组的维度,返回一个元组,这个元组的长度就是维度的数目,即 ndim 属性(秩)。
#numpy.ndarray.size数组中所有元素的总量,相当于数组的shape中所有元素的乘积,例如矩阵的元素总量为行
#与列的乘积。
#numpy.ndarray.dtype ndarray 对象的元素类型。
#numpy.ndarray.itemsize以字节的形式返回数组中每一个元素的大小。
a = np.array([1, 2, 3, 4, 5])
print(a.shape) # (5,)
print(a.dtype) # int32
print(a.size) # 5
print(a.ndim) # 1
print(a.itemsize) # 4
b = np.array([[1, 2, 3], [4, 5, 6.0]])
print(b.shape) # (2, 3)
print(b.dtype) # float64
print(b.size) # 6
print(b.ndim) # 2
print(b.itemsize) # 8
#在ndarray中所有元素必须是同一类型,否则会自动向下转换,int->float->str。
a = np.array([1, 2, 3, 4, 5])
print(a) # [1 2 3 4 5]
b = np.array([1, 2, 3, 4, '5'])
print(b) # ['1' '2' '3' '4' '5']
c = np.array([1, 2, 3, 4, 5.0])
print(c) # [1. 2. 3. 4. 5.]副本与视图
在 Numpy 中,尤其是在做数组运算或数组操作时,返回结果不是数组的 副本 就是 视图。
在 Numpy 中,所有赋值运算不会为数组和数组中的任何元素创建副本。
numpy.ndarray.copy() 函数创建一个副本。 对副本数据进行修改,不会影响到原始数据,它们物理内存不在同一位置。数组切片操作返回的对象只是原数组的视图。
视图(计算机数据库术语)_百度百科 (baidu.com)
索引与切片
整数索引
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
print(x[2]) # 3
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
print(x[2]) # [21 22 23 24 25]
print(x[2][1]) # 22
print(x[2, 1]) # 22#利用负数下标翻转数组
print(x[::-1]) # [8 7 6 5 4 3 2 1]切片索引
#切片操作是指抽取数组的一部分元素生成新数组。对 python 列表进行切片操作得到的数组是原数组的副本,而#对 Numpy 数据进行切片操作得到的数组则是指向相同缓冲区的视图。
[0:max:1]
#多维
[0:max:1, 0:max:1]dots 索引
#NumPy 允许使用...表示足够多的冒号来构建完整的索引列表。
x[1,2,...] 等于 x[1,2,:,:,:]
x[...,3] 等于 x[:,:,:,:,3]
x[4,...,5,:] 等于 x[4,:,:,5,:]整数数组索引
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
r = [0, 1, 2]
print(x[r])
# [1 2 3]
r = [0, 1, -1]
print(x[r])
# [1 2 8]
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
r = [0, 1, 2]
print(x[r])
# [[11 12 13 14 15]
# [16 17 18 19 20]
# [21 22 23 24 25]]
r = [0, 1, -1]
print(x[r])
# [[11 12 13 14 15]
# [16 17 18 19 20]
# [31 32 33 34 35]]
r = [0, 1, 2]
c = [2, 3, 4]
y = x[r, c]
print(y)
# [13 19 25]可以借助切片:与整数数组组合。
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = x[0:3, [1, 2, 2]]
print(y)
# [[12 13 13]
# [17 18 18]
# [22 23 23]] numpy.take
(a, indices, axis=None, out=None, mode='raise') Take elements from an array along an axis.
import numpy as np
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
r = [0, 1, 2]
print(np.take(x, r))
# [1 2 3]
r = [0, 1, -1]
print(np.take(x, r))
# [1 2 8]
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
r = [0, 1, 2]
print(np.take(x, r, axis=0))
# [[11 12 13 14 15]
# [16 17 18 19 20]
# [21 22 23 24 25]]
print(np.take(x, r, axis=1))
# [[11 12 13]
# [16 17 18]
# [21 22 23]
# [26 27 28]
# [31 32 33]]
r = [0, 1, -1]
print(np.take(x, r, axis=0))
# [[11 12 13 14 15]
# [16 17 18 19 20]
# [31 32 33 34 35]]
r = [0, 1, 2]
c = [2, 3, 4]
y = np.take(x, [r, c]) #按照list切两遍,每一遍为一个张量,拼接
print(y)
# [[11 12 13]
# [13 14 15]]使用切片索引到numpy数组时,生成的数组视图将始终是原始数组的子数组, 但是整数数组索引,不是其子数组,是形成新的数组。
#切片一个改了,都改变
import numpy as np
a=np.array([[1,2],[3,4],[5,6]])
b=a[0:1,0:1]
b[0,0]=2
print(a[0,0]==b)
#[[True]]
#数值索引一个改了,其他的不变
import numpy as np
a=np.array([[1,2],[3,4],[5,6]])
b=a[0,0]
b=2
print(a[0,0]==b)
#False布尔索引
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
y = x > 5
print(y)
# [False False False False False True True True]
print(x[x > 5])
# [6 7 8]去除数组中的空值
import numpy as np
x = np.array([np.nan, 1, 2, np.nan, 3, 4, 5])
y = np.logical_not(np.isnan(x))
print(x)
print(y)
print(x[y])
# [nan 1. 2. nan 3. 4. 5.]
# [False True True False True True True]
# [1. 2. 3. 4. 5.]
数组迭代
除了for循环,Numpy 还提供另外一种更为优雅的遍历方法。
apply_along_axis(func1d, axis, arr) Apply a function to 1-D slices along the given axis.
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = np.apply_along_axis(np.sum, 0, x)
print(y) # [105 110 115 120 125]
y = np.apply_along_axis(np.sum, 1, x)
print(y) # [ 65 90 115 140 165]
y = np.apply_along_axis(np.mean, 0, x)
print(y) # [21. 22. 23. 24. 25.]
y = np.apply_along_axis(np.mean, 1, x)
print(y) # [13. 18. 23. 28. 33.]
def my_func(x):
return (x[0] + x[-1]) * 0.5
y = np.apply_along_axis(my_func, 0, x)
print(y) # [21. 22. 23. 24. 25.]
y = np.apply_along_axis(my_func, 1, x)
print(y) # [13. 18. 23. 28. 33.]应用
import numpy as np
arr = np.arange(9).reshape(3, 3)
print(arr)
#交换1, 3列
print(arr[:, ::-1])
print(arr[:, [2, 1, 0]])
#交换1, 2行
print(arr[[1, 0, 2], :])
print(arr[[1, 0, 2]])
#反转所有行,
print(arr[::-1, :])
数组操作
更改形状
numpy.ndarray.shape
表示数组的维度,返回一个元组,这个元组的长度就是维度的数目,即 ndim 属性(秩)。
numpy.ndarray.flat
将数组转换为一维的迭代器,可以用for访问数组每一个元素。
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = x.flat
print(y)
#
for i in y:
print(i, end=' ')
# 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
y[3] = 0
print(end='\n')
print(x)
# [[11 12 13 0 15]
# [16 17 18 19 20]
# [21 22 23 24 25]
# [26 27 28 29 30]
# [31 32 33 34 35]] numpy.ndarray.flatten([order='C'])
order:'C' -- 按行,'F' -- 按列,'A' -- 原顺序,'k' -- 元素在内存中的出现顺序。(简记)
order:{'C / F,'A,K},可选使用此索引顺序读取a的元素。'C'意味着以行大的C风格顺序对元素进行索引,最后一个轴索引会更改F表示以列大的Fortran样式顺序索引元素,其中第一个索引变化最快,最后一个索引变化最快。请注意,'C'和'F'选项不考虑基础数组的内存布局,仅引用轴索引的顺序.A'表示如果a为Fortran,则以类似Fortran的索引顺序读取元素在内存中连续,否则类似C的顺序。“ K”表示按照步序在内存中的顺序读取元素,但步幅为负时反转数据除外。默认情况下,使用Cindex顺序。
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = x.flatten()
print(y)
# [11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
# 35]
y[3] = 0
print(x)
# [[11 12 13 14 15]
# [16 17 18 19 20]
# [21 22 23 24 25]
# [26 27 28 29 30]
# [31 32 33 34 35]]
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = x.flatten(order='F')
print(y)
# [11 16 21 26 31 12 17 22 27 32 13 18 23 28 33 14 19 24 29 34 15 20 25 30
# 35]
y[3] = 0
print(x)
# [[11 12 13 14 15]
# [16 17 18 19 20]
# [21 22 23 24 25]
# [26 27 28 29 30]
# [31 32 33 34 35]]umpy.ravel(a, order='C')
Return a contiguous flattened array.
#返回的是视图。
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = np.ravel(x)
print(y)
# [11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34
# 35]
y[3] = 0
print(x)
# [[11 12 13 0 15]
# [16 17 18 19 20]
# [21 22 23 24 25]
# [26 27 28 29 30]
# [31 32 33 34 35]]
#order=F 就是拷贝
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = np.ravel(x, order='F')
print(y)
# [11 16 21 26 31 12 17 22 27 32 13 18 23 28 33 14 19 24 29 34 15 20 25 30
# 35]
y[3] = 0
print(x)
# [[11 12 13 14 15]
# [16 17 18 19 20]
# [21 22 23 24 25]
# [26 27 28 29 30]
# [31 32 33 34 35]]numpy.reshape(a, newshape[, order='C'])
在不更改数据的情况下为数组赋予新的形状。
#reshape()函数当参数newshape = [rows,-1]时,将根据行数自动确定列数。
import numpy as np
x = np.arange(12)
y = np.reshape(x, [3, 4])
print(y.dtype) # int32
print(y)
# [[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
y = np.reshape(x, [3, -1])
print(y)
# [[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
y = np.reshape(x,[-1,3])
print(y)
# [[ 0 1 2]
# [ 3 4 5]
# [ 6 7 8]
# [ 9 10 11]]
y[0, 1] = 10
print(x)
# [ 0 10 2 3 4 5 6 7 8 9 10 11](改变x去reshape后y中的值,x对应元素也改变)
#reshape()函数当参数newshape = -1时,表示将数组降为一维。
import numpy as np
x = np.random.randint(12, size=[2, 2, 3])
print(x)
# [[[11 9 1]
# [ 1 10 3]]
#
# [[ 0 6 1]
# [ 4 11 3]]]
y = np.reshape(x, -1)
print(y)
# [11 9 1 1 10 3 0 6 1 4 11 3]
数组转置
numpy.transpose(a, axes=None)
Permute the dimensions of an array.
numpy.ndarray.T
Same as self.transpose(), except that self is returned if self.ndim < 2.
更改维度
numpy.newaxis
可以使用newaxis参数来增加一个维度。
import numpy as np
x = np.array([1, 2, 9, 4, 5, 6, 7, 8])
print(x.shape) # (8,)
print(x) # [1 2 9 4 5 6 7 8]
y = x[np.newaxis, :]
print(y.shape) # (1, 8)
print(y) # [[1 2 9 4 5 6 7 8]]
y = x[:, np.newaxis]
print(y.shape) # (8, 1)
print(y)
# [[1]
# [2]
# [9]
# [4]
# [5]
# [6]
# [7]
# [8]]numpy.squeeze(a, axis=None)
从数组的形状中删除单维度条目,即把shape中为1的维度去掉。
a表示输入的数组;axis用于指定需要删除的维度,但是指定的维度必须为单维度,否则将会报错;
import numpy as np
x = np.arange(10)
print(x.shape) # (10,)
x = x[np.newaxis, :]
print(x.shape) # (1, 10)
y = np.squeeze(x)
print(y.shape) # (10,)
import numpy as np
x = np.array([[[0], [1], [2]]])
print(x.shape) # (1, 3, 1)
print(x)
# [[[0]
# [1]
# [2]]]
y = np.squeeze(x)
print(y.shape) # (3,)
print(y) # [0 1 2]
y = np.squeeze(x, axis=0)
print(y.shape) # (3, 1)
print(y)
# [[0]
# [1]
# [2]]
y = np.squeeze(x, axis=2)
print(y.shape) # (1, 3)
print(y) # [[0 1 2]]
y = np.squeeze(x, axis=1)
# ValueError: cannot select an axis to squeeze out which has size not equal to one数组组合
numpy.concatenate((a1, a2, ...), axis=0, out=None)
Join a sequence of arrays along an existing axis.
#连接沿现有轴的数组序列(原来x,y都是一维的,拼接后的结果也是一维的)。
import numpy as np
x = np.array([1, 2, 3])
y = np.array([7, 8, 9])
z = np.concatenate([x, y])
print(z)
# [1 2 3 7 8 9]
z = np.concatenate([x, y], axis=0)
print(z)
# [1 2 3 7 8 9]
#原来x,y都是二维的,拼接后的结果也是二维的。
import numpy as np
x = np.array([1, 2, 3]).reshape(1, 3)
y = np.array([7, 8, 9]).reshape(1, 3)
z = np.concatenate([x, y])
print(z)
# [[ 1 2 3]
# [ 7 8 9]]
z = np.concatenate([x, y], axis=0)
print(z)
# [[ 1 2 3]
# [ 7 8 9]]
z = np.concatenate([x, y], axis=1)
print(z)
#x,y在原来的维度上进行拼接。
import numpy as np
x = np.array([[1, 2, 3], [4, 5, 6]])
y = np.array([[7, 8, 9], [10, 11, 12]])
z = np.concatenate([x, y])
print(z)
# [[ 1 2 3]
# [ 4 5 6]
# [ 7 8 9]
# [10 11 12]]
z = np.concatenate([x, y], axis=0)
print(z)
# [[ 1 2 3]
# [ 4 5 6]
# [ 7 8 9]
# [10 11 12]]
z = np.concatenate([x, y], axis=1)
print(z)
# [[ 1 2 3 7 8 9]
# [ 4 5 6 10 11 12]]numpy.stack(arrays, axis=0, out=None)
Join a sequence of arrays along a new axis.
#沿着新的轴加入一系列数组(stack为增加维度的拼接)。
import numpy as np
x = np.array([1, 2, 3])
y = np.array([7, 8, 9])
z = np.stack([x, y])
print(z.shape) # (2, 3)
print(z)
# [[1 2 3]
# [7 8 9]]
z = np.stack([x, y], axis=1)
print(z.shape) # (3, 2)
print(z)
# [[1 7]
# [2 8]
# [3 9]]
#
import numpy as np
x = np.array([1, 2, 3]).reshape(1, 3)
y = np.array([7, 8, 9]).reshape(1, 3)
z = np.stack([x, y])
print(z.shape) # (2, 1, 3)
print(z)
# [[[1 2 3]]
#
# [[7 8 9]]]
z = np.stack([x, y], axis=1)
print(z.shape) # (1, 2, 3)
print(z)
# [[[1 2 3]
# [7 8 9]]]
z = np.stack([x, y], axis=2)
print(z.shape) # (1, 3, 2)
print(z)
# [[[1 7]
# [2 8]
# [3 9]]]
#
import numpy as np
x = np.array([1, 2, 3]).reshape(1, 3)
y = np.array([7, 8, 9]).reshape(1, 3)
z = np.stack([x, y])
print(z.shape) # (2, 1, 3)
print(z)
# [[[1 2 3]]
#
# [[7 8 9]]]
z = np.stack([x, y], axis=1)
print(z.shape) # (1, 2, 3)
print(z)
# [[[1 2 3]
# [7 8 9]]]
z = np.stack([x, y], axis=2)
print(z.shape) # (1, 3, 2)
print(z)
# [[[1 7]
# [2 8]
# [3 9]]]
#
import numpy as np
x = np.array([[1, 2, 3], [4, 5, 6]])
y = np.array([[7, 8, 9], [10, 11, 12]])
z = np.stack([x, y])
print(z.shape) # (2, 2, 3)
print(z)
# [[[ 1 2 3]
# [ 4 5 6]]
#
# [[ 7 8 9]
# [10 11 12]]]
z = np.stack([x, y], axis=1)
print(z.shape) # (2, 2, 3)
print(z)
# [[[ 1 2 3]
# [ 7 8 9]]
#
# [[ 4 5 6]
# [10 11 12]]]
z = np.stack([x, y], axis=2)
print(z.shape) # (2, 3, 2)
print(z)
# [[[ 1 7]
# [ 2 8]
# [ 3 9]]
#
# [[ 4 10]
# [ 5 11]
# [ 6 12]]]
numpy.vstack(tup)
Stack arrays in sequence vertically (row wise).
numpy.hstack(tup)
Stack arrays in sequence horizontally (column wise).
#一维
import numpy as np
x = np.array([1, 2, 3])
y = np.array([7, 8, 9])
z = np.vstack((x, y))
print(z.shape) # (2, 3)
print(z)
# [[1 2 3]
# [7 8 9]]
z = np.stack([x, y])
print(z.shape) # (2, 3)
print(z)
# [[1 2 3]
# [7 8 9]]
z = np.hstack((x, y))
print(z.shape) # (6,)
print(z)
# [1 2 3 7 8 9]
z = np.concatenate((x, y))
print(z.shape) # (6,)
print(z) # [1 2 3 7 8 9]
#二位
import numpy as np
x = np.array([1, 2, 3]).reshape(1, 3)
y = np.array([7, 8, 9]).reshape(1, 3)
z = np.vstack((x, y))
print(z.shape) # (2, 3)
print(z)
# [[1 2 3]
# [7 8 9]]
z = np.concatenate((x, y), axis=0)
print(z.shape) # (2, 3)
print(z)
# [[1 2 3]
# [7 8 9]]
z = np.hstack((x, y))
print(z.shape) # (1, 6)
print(z)
# [[ 1 2 3 7 8 9]]
z = np.concatenate((x, y), axis=1)
print(z.shape) # (1, 6)
print(z)
# [[1 2 3 7 8 9]]
#
import numpy as np
x = np.array([[1, 2, 3], [4, 5, 6]])
y = np.array([[7, 8, 9], [10, 11, 12]])
z = np.vstack((x, y))
print(z.shape) # (4, 3)
print(z)
# [[ 1 2 3]
# [ 4 5 6]
# [ 7 8 9]
# [10 11 12]]
z = np.concatenate((x, y), axis=0)
print(z.shape) # (4, 3)
print(z)
# [[ 1 2 3]
# [ 4 5 6]
# [ 7 8 9]
# [10 11 12]]
z = np.hstack((x, y))
print(z.shape) # (2, 6)
print(z)
# [[ 1 2 3 7 8 9]
# [ 4 5 6 10 11 12]]
z = np.concatenate((x, y), axis=1)
print(z.shape) # (2, 6)
print(z)
# [[ 1 2 3 7 8 9]
# [ 4 5 6 10 11 12]]hstack(),vstack()分别表示水平和竖直的拼接方式。在数据维度等于1时,比较特殊。而当维度大于或等于2时,它们的作用相当于concatenate,用于在已有轴上进行操作。
import numpy as np
a = np.hstack([np.array([1, 2, 3, 4]), 5])
print(a) # [1 2 3 4 5]
a = np.concatenate([np.array([1, 2, 3, 4]), 5])
print(a)
# all the input arrays must have same number of dimensions, but the array at index 0 has 1 dimension(s) and the array at index 1 has 0 dimension(s)
#5 标量 0维数组拆分
numpy.split(ary, indices_or_sections, axis=0)
Split an array into multiple sub-arrays as views into ary.
把一个数组从左到右按顺序切分
参数:
ary:要切分的数组
indices_or_sections:如果是一个整数,就用该数平均切分,如果是一个数组,为沿轴切分的位置(左开右闭)
axis:沿着哪个维度进行切向,默认为0,横向切分。为1时,纵向切分
>>> x = np.arange(9.0)
>>> np.split(x, 3)
[array([ 0., 1., 2.]), array([ 3., 4., 5.]), array([ 6., 7., 8.])]
>>> x = np.arange(8.0)
>>> np.split(x, [3, 5, 6, 10])
[array([ 0., 1., 2.]),
array([ 3., 4.]),
array([ 5.]),
array([ 6., 7.]),
array([], dtype=float64)]
#(3, )
m = np.arange(8.0)
n = np.split(m, (3,))
print(n)
结果:[array([0., 1., 2.]), array([3., 4., 5., 6., 7.])]
机器学习中的用法解释:
#axis=1,代表列,是要把data数据集中的所有数据按第四、五列之间分割为X集和Y集。
x, y = np.split(data, (4,), axis=1)
#
import numpy as np
# Test 1
A = np.arange(12).reshape(3, 4)
print A
# 纵向分割, 分成两部分, 按列分割
print np.split(A, 2, axis = 1)
# 横向分割, 分成三部分, 按行分割
print np.split(A, 3, axis = 0)
# Test 1 result
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[array([[0, 1],
[4, 5],
[8, 9]]), array([[ 2, 3],
[ 6, 7],
[10, 11]])]
[array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8, 9, 10, 11]])]
# Test 2
# 不均等分割
print np.array_split(A, 3, axis = 1)
# Test 2 result
[array([[0, 1],
[4, 5],
[8, 9]]), array([[ 2],
[ 6],
[10]]), array([[ 3],
[ 7],
[11]])]
In [5]:
# Test 3
# 垂直方向分割
print np.vsplit(A, 3)
# 水平方向分割
print np.hsplit(A, 2)
# Test 3 result
[array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8, 9, 10, 11]])]
[array([[0, 1],
[4, 5],
[8, 9]]), array([[ 2, 3],
[ 6, 7],
[10, 11]])]split必须要均等分,否则会报错。array_split不会
import numpy as np
x = np.arange(8.0)
print np.array_split(x,3)
print np.split(x, 3)numpy.vsplit(ary, indices_or_sections)
Split an array into multiple sub-arrays vertically (row-wise).
#垂直切分是把数组按照高度切分
import numpy as np
x = np.array([[11, 12, 13, 14],
[16, 17, 18, 19],
[21, 22, 23, 24]])
y = np.vsplit(x, 3)
print(y)
# [array([[11, 12, 13, 14]]), array([[16, 17, 18, 19]]), array([[21, 22, 23, 24]])]
y = np.split(x, 3)
print(y)
# [array([[11, 12, 13, 14]]), array([[16, 17, 18, 19]]), array([[21, 22, 23, 24]])]
y = np.vsplit(x, [1])
print(y)
# [array([[11, 12, 13, 14]]), array([[16, 17, 18, 19],
# [21, 22, 23, 24]])]
y = np.split(x, [1])
print(y)
# [array([[11, 12, 13, 14]]), array([[16, 17, 18, 19],
# [21, 22, 23, 24]])]
y = np.vsplit(x, [1, 3])
print(y)
# [array([[11, 12, 13, 14]]), array([[16, 17, 18, 19],
# [21, 22, 23, 24]]), array([], shape=(0, 4), dtype=int32)]
y = np.split(x, [1, 3], axis=0)
print(y)
# [array([[11, 12, 13, 14]]), array([[16, 17, 18, 19],
# [21, 22, 23, 24]]), array([], shape=(0, 4), dtype=int32)]numpy.hsplit(ary, indices_or_sections)
Split an array into multiple sub-arrays horizontally (column-wise).
#水平切分是把数组按照宽度切分。
import numpy as np
x = np.array([[11, 12, 13, 14],
[16, 17, 18, 19],
[21, 22, 23, 24]])
y = np.hsplit(x, 2)
print(y)
# [array([[11, 12],
# [16, 17],
# [21, 22]]), array([[13, 14],
# [18, 19],
# [23, 24]])]
y = np.split(x, 2, axis=1)
print(y)
# [array([[11, 12],
# [16, 17],
# [21, 22]]), array([[13, 14],
# [18, 19],
# [23, 24]])]
y = np.hsplit(x, [3])
print(y)
# [array([[11, 12, 13],
# [16, 17, 18],
# [21, 22, 23]]), array([[14],
# [19],
# [24]])]
y = np.split(x, [3], axis=1)
print(y)
# [array([[11, 12, 13],
# [16, 17, 18],
# [21, 22, 23]]), array([[14],
# [19],
# [24]])]
y = np.hsplit(x, [1, 3])
print(y)
# [array([[11],
# [16],
# [21]]), array([[12, 13],
# [17, 18],
# [22, 23]]), array([[14],
# [19],
# [24]])]
y = np.split(x, [1, 3], axis=1)
print(y)
# [array([[11],
# [16],
# [21]]), array([[12, 13],
# [17, 18],
# [22, 23]]), array([[14],
# [19],
# [24]])]数组平铺
numpy.tile(A, reps)
Construct an array by repeating A the number of times given by reps.
#将原矩阵横向、纵向地复制。
import numpy as np
x = np.array([[1, 2], [3, 4]])
print(x)
# [[1 2]
# [3 4]]
y = np.tile(x, (1, 3))
print(y)
# [[1 2 1 2 1 2]
# [3 4 3 4 3 4]]
y = np.tile(x, (3, 1))
print(y)
# [[1 2]
# [3 4]
# [1 2]
# [3 4]
# [1 2]
# [3 4]]
y = np.tile(x, (3, 3))
print(y)
# [[1 2 1 2 1 2]
# [3 4 3 4 3 4]
# [1 2 1 2 1 2]
# [3 4 3 4 3 4]
# [1 2 1 2 1 2]
# [3 4 3 4 3 4]]numpy.repeat(a, repeats, axis=None)
Repeat elements of an array.
axis=0,沿着y轴复制,实际上增加了行数。axis=1,沿着x轴复制,实际上增加了列数。repeats,可以为一个数,也可以为一个矩阵。axis=None时就会flatten当前矩阵,实际上就是变成了一个行向量。
import numpy as np
x = np.repeat(3, 4)
print(x) # [3 3 3 3]
x = np.array([[1, 2], [3, 4]])
y = np.repeat(x, 2)
print(y)
# [1 1 2 2 3 3 4 4]
y = np.repeat(x, 2, axis=0)
print(y)
# [[1 2]
# [1 2]
# [3 4]
# [3 4]]
y = np.repeat(x, 2, axis=1)
print(y)
# [[1 1 2 2]
# [3 3 4 4]]
y = np.repeat(x, [2, 3], axis=0)
print(y)
# [[1 2]
# [1 2]
# [3 4]
# [3 4]
# [3 4]]
y = np.repeat(x, [2, 3], axis=1)
print(y)
# [[1 1 2 2 2]
# [3 3 4 4 4]]添加和删除元素
np.unique
对于一维数组或者列表,unique函数去除其中重复的元素,并按元素由大到小返回一个新的无元素重复的元组或者列表
#a = np.unique(A)
import numpy as np
A = [1, 2, 2, 5,3, 4, 3]
a = np.unique(A)
B= (1, 2, 2,5, 3, 4, 3)
b= np.unique(B)
C= ['fgfh','asd','fgfh','asdfds','wrh']
c= np.unique(C)
print(a)
print(b)
print(c)
# 输出为 [1 2 3 4 5]
# [1 2 3 4 5]
# ['asd' 'asdfds' 'fgfh' 'wrh']
#c,s=np.unique(b,return_index=True)
#return_index=True表示返回新列表元素在旧列表中的位置,并以列表形式储存在s中。
a, s= np.unique(A, return_index=True)
print(a)
print(s)
# 运行结果
# [1 2 3 4 5]
# [0 1 4 5 3]
#a, s,p = np.unique(A, return_index=True, return_inverse=True)
#return_inverse=True 表示返回旧列表元素在新列表中的位置,并以列表形式储存在p中
a, s,p = np.unique(A, return_index=True, return_inverse=True)
print(a)
print(s)
print(p)
# 运行结果
# [1 2 3 4 5]
# [0 1 4 5 3]
# [0 1 1 4 2 3 2]应用
#将 arr的2维数组按列输出。
import numpy as np
arr = np.array([[16, 17, 18, 19, 20],[11, 12, 13, 14, 15],[21, 22, 23, 24, 25],[31, 32, 33, 34, 35],[26, 27, 28, 29, 30]])
y = arr.flatten(order='F')
print(y)
arr = np.array([[16, 17, 18, 19, 20],[11, 12, 13, 14, 15],[21, 22, 23, 24, 25],[31, 32, 33, 34, 35],[26, 27, 28, 29, 30]])
for item in arr.T.flat:
print(item)给定两个随机数组A和B,验证它们是否相等。
import numpy as np
A = np.array([1,2,3])
B = np.array([1,2,3])
# Assuming identical shape of the arrays and a tolerance for the comparison of values
equal = np.allclose(A,B)
print(equal)
# Checking both the shape and the element values, no tolerance (values have to be exactly equal)
equal = np.array_equal(A,B)
print(equal)在给定的numpy数组中找到重复的条目(第二次出现以后),并将它们标记为True。第一次出现应为False。
import numpy as np
np.random.seed(100)
a = np.random.randint(0, 5, 10)
print(a)
# [0 0 3 0 2 4 2 2 2 2]
b = np.full(10, True)
vals, counts = np.unique(a, return_index=True)
b[counts] = False
print(b)
# [False True False True False False True True True True]逻辑函数
真值测试
numpy.all
numpy.any
numpy.all(a, axis=None, out=None, keepdims=np._NoValue)Test whether all array elements along a given axis evaluate to True.numpy.any(a, axis=None, out=None, keepdims=np._NoValue)Test whether any array element along a given axis evaluates to True.
import numpy as np
a = np.array([0, 4, 5])
b = np.copy(a)
print(np.all(a == b)) # True
print(np.any(a == b)) # True
b[0] = 1
print(np.all(a == b)) # False
print(np.any(a == b)) # True
print(np.all([1.0, np.nan])) # True
print(np.any([1.0, np.nan])) # True
a = np.eye(3)
print(np.all(a, axis=0)) # [False False False]
print(np.any(a, axis=0)) # [ True True True]数组内容
numpy.isnan
numpy.isnan(x, *args, **kwargs)Test element-wise for NaN and return result as a boolean array.
a=np.array([1,2,np.nan])
print(np.isnan(a))
#[False False True]逻辑运算
numpy.logical_not
numpy.logical_and
numpy.logical_or
numpy.logical_xor
numpy.logical_not(x, *args, **kwargs)Compute the truth value of NOT x element-wise.numpy.logical_and(x1, x2, *args, **kwargs)Compute the truth value of x1 AND x2 element-wise.numpy.logical_or(x1, x2, *args, **kwargs)Compute the truth value of x1 OR x2 element-wise.numpy.logical_xor(x1, x2, *args, **kwargs)Compute the truth value of x1 XOR x2, element-wise.
import numpy as np
print(np.logical_not(3))
# False
print(np.logical_not([True, False, 0, 1]))
# [False True True False]
x = np.arange(5)
print(np.logical_not(x < 3))
# [False False False True True]print(np.logical_and(True, False))
# False
print(np.logical_and([True, False], [True, False]))
# [ True False]
print(np.logical_and(x > 1, x < 4))
# [False False True True False]print(np.logical_or(True, False))
# True
print(np.logical_or([True, False], [False, False]))
# [ True False]
print(np.logical_or(x < 1, x > 3))
# [ True False False False True]print(np.logical_or(True, False))
# True
print(np.logical_or([True, False], [False, False]))
# [ True False]
print(np.logical_or(x < 1, x > 3))
# [ True False False False True]对照
numpy.greater
numpy.greater_equal
numpy.equal
numpy.not_equal
numpy.less
numpy.less_equa
numpy.greater(x1, x2, *args, **kwargs)Return the truth value of (x1 > x2) element-wise.numpy.greater_equal(x1, x2, *args, **kwargs)Return the truth value of (x1 >= x2) element-wise.numpy.equal(x1, x2, *args, **kwargs)Return (x1 == x2) element-wise.numpy.not_equal(x1, x2, *args, **kwargs)Return (x1 != x2) element-wise.numpy.less(x1, x2, *args, **kwargs)Return the truth value of (x1 < x2) element-wise.numpy.less_equal(x1, x2, *args, **kwargs)Return the truth value of (x1 =< x2) element-wise.
#numpy对以上对照函数进行了运算符的重载。
import numpy as np
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
y = x > 2
print(y)
print(np.greater(x, 2))
# [False False True True True True True True]
y = x >= 2
print(y)
print(np.greater_equal(x, 2))
# [False True True True True True True True]
y = x == 2
print(y)
print(np.equal(x, 2))
# [False True False False False False False False]
y = x != 2
print(y)
print(np.not_equal(x, 2))
# [ True False True True True True True True]
y = x < 2
print(y)
print(np.less(x, 2))
# [ True False False False False False False False]
y = x <= 2
print(y)
print(np.less_equal(x, 2))
# [ True True False False False False False False]
#例
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = x > 20
print(y)
print(np.greater(x, 20))
# [[False False False False False]
# [False False False False False]
# [ True True True True True]
# [ True True True True True]
# [ True True True True True]]
y = x >= 20
print(y)
print(np.greater_equal(x, 20))
# [[False False False False False]
# [False False False False True]
# [ True True True True True]
# [ True True True True True]
# [ True True True True True]]
y = x == 20
print(y)
print(np.equal(x, 20))
# [[False False False False False]
# [False False False False True]
# [False False False False False]
# [False False False False False]
# [False False False False False]]
y = x != 20
print(y)
print(np.not_equal(x, 20))
# [[ True True True True True]
# [ True True True True False]
# [ True True True True True]
# [ True True True True True]
# [ True True True True True]]
y = x < 20
print(y)
print(np.less(x, 20))
# [[ True True True True True]
# [ True True True True False]
# [False False False False False]
# [False False False False False]
# [False False False False False]]
y = x <= 20
print(y)
print(np.less_equal(x, 20))
# [[ True True True True True]
# [ True True True True True]
# [False False False False False]
# [False False False False False]
# [False False False False False]]
注意 numpy 的广播规则。
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
np.random.seed(20200611)
y = np.random.randint(10, 50, 5)
print(y)
# [32 37 30 24 10]
z = x > y
print(z)
print(np.greater(x, y))
# [[False False False False True]
# [False False False False True]
# [False False False False True]
# [False False False True True]
# [False False True True True]]
z = x >= y
print(z)
print(np.greater_equal(x, y))
# [[False False False False True]
# [False False False False True]
# [False False False True True]
# [False False False True True]
# [False False True True True]]
z = x == y
print(z)
print(np.equal(x, y))
# [[False False False False False]
# [False False False False False]
# [False False False True False]
# [False False False False False]
# [False False False False False]]
z = x != y
print(z)
print(np.not_equal(x, y))
# [[ True True True True True]
# [ True True True True True]
# [ True True True False True]
# [ True True True True True]
# [ True True True True True]]
z = x < y
print(z)
print(np.less(x, y))
# [[ True True True True False]
# [ True True True True False]
# [ True True True False False]
# [ True True True False False]
# [ True True False False False]]
z = x <= y
print(z)
print(np.less_equal(x, y))
# [[ True True True True False]
# [ True True True True False]
# [ True True True True False]
# [ True True True False False]
# [ True True False False False]]numpy.isclose
numpy.allclose
numpy.isclose(a, b, rtol=1.e-5, atol=1.e-8, equal_nan=False)Returns a boolean array where two arrays are element-wise equal within a tolerance.numpy.allclose(a, b, rtol=1.e-5, atol=1.e-8, equal_nan=False)Returns True if two arrays are element-wise equal within a tolerance.
返回一个布尔数组,其中两个数组在容差范围内元素相等。
如果两个数组在容差范围内元素相等,则返回 True。
numpy.allclose() 等价于 numpy.all(isclose(a, b, rtol=rtol, atol=atol, equal_nan=equal_nan))
判断公式
absolute(a - b) <= (atol + rtol * absolute(b))
import numpy as np
x = np.isclose([1e10, 1e-7], [1.00001e10, 1e-8])
print(x) # [ True False]
x = np.allclose([1e10, 1e-7], [1.00001e10, 1e-8])
print(x) # False
x = np.isclose([1e10, 1e-8], [1.00001e10, 1e-9])
print(x) # [ True True]
x = np.allclose([1e10, 1e-8], [1.00001e10, 1e-9])
print(x) # True
x = np.isclose([1e10, 1e-8], [1.0001e10, 1e-9])
print(x) # [False True]
x = np.allclose([1e10, 1e-8], [1.0001e10, 1e-9])
print(x) # False
x = np.isclose([1.0, np.nan], [1.0, np.nan])
print(x) # [ True False]
x = np.allclose([1.0, np.nan], [1.0, np.nan])
print(x) # False
x = np.isclose([1.0, np.nan], [1.0, np.nan], equal_nan=True)
print(x) # [ True True]
x = np.allclose([1.0, np.nan], [1.0, np.nan], equal_nan=True)
print(x) # True向量化和广播
向量化和广播这两个概念是 numpy 内部实现的基础。有了向量化,编写代码时无需使用显式循环。这些循环实际上不能省略,只不过是在内部实现,被代码中的其他结构代替。向量化的应用使得代码更简洁,可读性更强,也可以说使用了向量化方法的代码看上去更“Pythonic”。
广播(Broadcasting)机制描述了 numpy 如何在算术运算期间处理具有不同形状的数组,让较小的数组在较大的数组上“广播”,以便它们具有兼容的形状。并不是所有的维度都要彼此兼容才符合广播机制的要求,但它们必须满足一定的条件。
若两个数组的各维度兼容,也就是两个数组的每一维等长,或其中一个数组为 一维,那么广播机制就适用。如果这两个条件不满足,numpy就会抛出异常,说两个数组不兼容。
总结来说,广播的规则有三个:
- 如果两个数组的维度数dim不相同,那么小维度数组的形状将会在左边补1。
- 如果shape维度不匹配,但是有维度是1,那么可以扩展维度是1的维度匹配另一个数组;
- 如果shape维度不匹配,但是没有任何一个维度是1,则匹配引发错误;
#二维数组加一维数组
import numpy as np
x = np.arange(4)
y = np.ones((3, 4))
print(x.shape) # (4,)
print(y.shape) # (3, 4)
print((x + y).shape) # (3, 4)
print(x + y)
# [[1. 2. 3. 4.]
# [1. 2. 3. 4.]
# [1. 2. 3. 4.]]
#两个数组均需要广播
import numpy as np
x = np.arange(4).reshape(4, 1)
y = np.ones(5)
print(x.shape) # (4, 1)
print(y.shape) # (5,)
print((x + y).shape) # (4, 5)
print(x + y)
# [[1. 1. 1. 1. 1.]
# [2. 2. 2. 2. 2.]
# [3. 3. 3. 3. 3.]
# [4. 4. 4. 4. 4.]]
x = np.array([0.0, 10.0, 20.0, 30.0])
y = np.array([1.0, 2.0, 3.0])
z = x[:, np.newaxis] + y
print(z)
# [[ 1. 2. 3.]
# [11. 12. 13.]
# [21. 22. 23.]
# [31. 32. 33.]]
#不匹配报错的例子
import numpy as np
x = np.arange(4)
y = np.ones(5)
print(x.shape) # (4,)
print(y.shape) # (5,)
print(x + y)
# ValueError: operands could not be broadcast together with shapes (4,) (5,)
数学函数
算数运算
向量化和广播
向量化和广播这两个概念是 numpy 内部实现的基础。有了向量化,编写代码时无需使用显式循环。这些循环实际上不能省略,只不过是在内部实现,被代码中的其他结构代替。向量化的应用使得代码更简洁,可读性更强,也可以说使用了向量化方法的代码看上去更“Pythonic”。
广播(Broadcasting)机制描述了 numpy 如何在算术运算期间处理具有不同形状的数组,让较小的数组在较大的数组上“广播”,以便它们具有兼容的形状。并不是所有的维度都要彼此兼容才符合广播机制的要求,但它们必须满足一定的条件。
若两个数组的各维度兼容,也就是两个数组的每一维等长,或其中一个数组为 一维,那么广播机制就适用。如果这两个条件不满足,numpy就会抛出异常,说两个数组不兼容。
总结来说,广播的规则有三个:
- 如果两个数组的维度数dim不相同,那么小维度数组的形状将会在左边补1。
- 如果shape维度不匹配,但是有维度是1,那么可以扩展维度是1的维度匹配另一个数组;
- 如果shape维度不匹配,但是没有任何一个维度是1,则匹配引发错误;
【例】二维数组加一维数组
import numpy as np
x = np.arange(4)
y = np.ones((3, 4))
print(x.shape) # (4,)
print(y.shape) # (3, 4)
print((x + y).shape) # (3, 4)
print(x + y)
# [[1. 2. 3. 4.]
# [1. 2. 3. 4.]
# [1. 2. 3. 4.]]【例】两个数组均需要广播
import numpy as np
x = np.arange(4).reshape(4, 1)
y = np.ones(5)
print(x.shape) # (4, 1)
print(y.shape) # (5,)
print((x + y).shape) # (4, 5)
print(x + y)
# [[1. 1. 1. 1. 1.]
# [2. 2. 2. 2. 2.]
# [3. 3. 3. 3. 3.]
# [4. 4. 4. 4. 4.]]
x = np.array([0.0, 10.0, 20.0, 30.0])
y = np.array([1.0, 2.0, 3.0])
z = x[:, np.newaxis] + y
print(z)
# [[ 1. 2. 3.]
# [11. 12. 13.]
# [21. 22. 23.]
# [31. 32. 33.]]【例】不匹配报错的例子
import numpy as np
x = np.arange(4)
y = np.ones(5)
print(x.shape) # (4,)
print(y.shape) # (5,)
print(x + y)
# ValueError: operands could not be broadcast together with shapes (4,) (5,) 数学函数
算数运算
numpy.add
numpy.subtract
numpy.multiply
numpy.divide
numpy.floor_divide
numpy.power
numpy.add(x1, x2, *args, **kwargs)Add arguments element-wise.numpy.subtract(x1, x2, *args, **kwargs)Subtract arguments element-wise.numpy.multiply(x1, x2, *args, **kwargs)Multiply arguments element-wise.numpy.divide(x1, x2, *args, **kwargs)Returns a true division of the inputs, element-wise.numpy.floor_divide(x1, x2, *args, **kwargs)Return the largest integer smaller or equal to the division of the inputs.numpy.power(x1, x2, *args, **kwargs)First array elements raised to powers from second array, element-wise.
在 numpy 中对以上函数进行了运算符的重载,且运算符为 元素级。也就是说,它们只用于位置相同的元素之间,所得到的运算结果组成一个新的数组。
import numpy as np
x = np.array([1, 2, 3, 4, 5, 6, 7, 8])
y = x + 1
print(y)
print(np.add(x, 1))
# [2 3 4 5 6 7 8 9]
y = x - 1
print(y)
print(np.subtract(x, 1))
# [0 1 2 3 4 5 6 7]
y = x * 2
print(y)
print(np.multiply(x, 2))
# [ 2 4 6 8 10 12 14 16]
y = x / 2
print(y)
print(np.divide(x, 2))
# [0.5 1. 1.5 2. 2.5 3. 3.5 4. ]
y = x // 2
print(y)
print(np.floor_divide(x, 2))
# [0 1 1 2 2 3 3 4]
y = x ** 2
print(y)
print(np.power(x, 2))
# [ 1 4 9 16 25 36 49 64]import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = x + 1
print(y)
print(np.add(x, 1))
# [[12 13 14 15 16]
# [17 18 19 20 21]
# [22 23 24 25 26]
# [27 28 29 30 31]
# [32 33 34 35 36]]
y = x - 1
print(y)
print(np.subtract(x, 1))
# [[10 11 12 13 14]
# [15 16 17 18 19]
# [20 21 22 23 24]
# [25 26 27 28 29]
# [30 31 32 33 34]]
y = x * 2
print(y)
print(np.multiply(x, 2))
# [[22 24 26 28 30]
# [32 34 36 38 40]
# [42 44 46 48 50]
# [52 54 56 58 60]
# [62 64 66 68 70]]
y = x / 2
print(y)
print(np.divide(x, 2))
# [[ 5.5 6. 6.5 7. 7.5]
# [ 8. 8.5 9. 9.5 10. ]
# [10.5 11. 11.5 12. 12.5]
# [13. 13.5 14. 14.5 15. ]
# [15.5 16. 16.5 17. 17.5]]
y = x // 2
print(y)
print(np.floor_divide(x, 2))
# [[ 5 6 6 7 7]
# [ 8 8 9 9 10]
# [10 11 11 12 12]
# [13 13 14 14 15]
# [15 16 16 17 17]]
y = x ** 2
print(y)
print(np.power(x, 2))
# [[ 121 144 169 196 225]
# [ 256 289 324 361 400]
# [ 441 484 529 576 625]
# [ 676 729 784 841 900]
# [ 961 1024 1089 1156 1225]]
#
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = np.arange(1, 6)
print(y)
# [1 2 3 4 5]
z = x + y
print(z)
print(np.add(x, y))
# [[12 14 16 18 20]
# [17 19 21 23 25]
# [22 24 26 28 30]
# [27 29 31 33 35]
# [32 34 36 38 40]]
z = x - y
print(z)
print(np.subtract(x, y))
# [[10 10 10 10 10]
# [15 15 15 15 15]
# [20 20 20 20 20]
# [25 25 25 25 25]
# [30 30 30 30 30]]
z = x * y
print(z)
print(np.multiply(x, y))
# [[ 11 24 39 56 75]
# [ 16 34 54 76 100]
# [ 21 44 69 96 125]
# [ 26 54 84 116 150]
# [ 31 64 99 136 175]]
z = x / y
print(z)
print(np.divide(x, y))
# [[11. 6. 4.33333333 3.5 3. ]
# [16. 8.5 6. 4.75 4. ]
# [21. 11. 7.66666667 6. 5. ]
# [26. 13.5 9.33333333 7.25 6. ]
# [31. 16. 11. 8.5 7. ]]
z = x // y
print(z)
print(np.floor_divide(x, y))
# [[11 6 4 3 3]
# [16 8 6 4 4]
# [21 11 7 6 5]
# [26 13 9 7 6]
# [31 16 11 8 7]]
z = x ** np.full([1, 5], 2)
print(z)
print(np.power(x, np.full([5, 5], 2)))
# [[ 121 144 169 196 225]
# [ 256 289 324 361 400]
# [ 441 484 529 576 625]
# [ 676 729 784 841 900]
# [ 961 1024 1089 1156 1225]]
#
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = np.arange(1, 26).reshape([5, 5])
print(y)
# [[ 1 2 3 4 5]
# [ 6 7 8 9 10]
# [11 12 13 14 15]
# [16 17 18 19 20]
# [21 22 23 24 25]]
z = x + y
print(z)
print(np.add(x, y))
# [[12 14 16 18 20]
# [22 24 26 28 30]
# [32 34 36 38 40]
# [42 44 46 48 50]
# [52 54 56 58 60]]
z = x - y
print(z)
print(np.subtract(x, y))
# [[10 10 10 10 10]
# [10 10 10 10 10]
# [10 10 10 10 10]
# [10 10 10 10 10]
# [10 10 10 10 10]]
z = x * y
print(z)
print(np.multiply(x, y))
# [[ 11 24 39 56 75]
# [ 96 119 144 171 200]
# [231 264 299 336 375]
# [416 459 504 551 600]
# [651 704 759 816 875]]
z = x / y
print(z)
print(np.divide(x, y))
# [[11. 6. 4.33333333 3.5 3. ]
# [ 2.66666667 2.42857143 2.25 2.11111111 2. ]
# [ 1.90909091 1.83333333 1.76923077 1.71428571 1.66666667]
# [ 1.625 1.58823529 1.55555556 1.52631579 1.5 ]
# [ 1.47619048 1.45454545 1.43478261 1.41666667 1.4 ]]
z = x // y
print(z)
print(np.floor_divide(x, y))
# [[11 6 4 3 3]
# [ 2 2 2 2 2]
# [ 1 1 1 1 1]
# [ 1 1 1 1 1]
# [ 1 1 1 1 1]]
z = x ** np.full([5, 5], 2)
print(z)
print(np.power(x, np.full([5, 5], 2)))
# [[ 121 144 169 196 225]
# [ 256 289 324 361 400]
# [ 441 484 529 576 625]
# [ 676 729 784 841 900]
# [ 961 1024 1089 1156 1225]]numpy.sqrt
numpy.square
numpy.sqrt(x, *args, **kwargs)Return the non-negative square-root of an array, element-wise.numpy.square(x, *args, **kwargs)Return the element-wise square of the input.
import numpy as np
x = np.arange(1, 5)
print(x) # [1 2 3 4]
y = np.sqrt(x)
print(y)
# [1. 1.41421356 1.73205081 2. ]
print(np.power(x, 0.5))
# [1. 1.41421356 1.73205081 2. ]
y = np.square(x)
print(y)
# [ 1 4 9 16]
print(np.power(x, 2))
# [ 1 4 9 16]三角函数
numpy.sin
numpy.cos
numpy.tan
numpy.arcsin
numpy.arccos
numpy.arctan
numpy.sin(x, *args, **kwargs)Trigonometric sine, element-wise.numpy.cos(x, *args, **kwargs)Cosine element-wise.numpy.tan(x, *args, **kwargs)Compute tangent element-wise.numpy.arcsin(x, *args, **kwargs)Inverse sine, element-wise.numpy.arccos(x, *args, **kwargs)Trigonometric inverse cosine, element-wise.numpy.arctan(x, *args, **kwargs)Trigonometric inverse tangent, element-wise.
通用函数(universal function)通常叫作ufunc,它对数组中的各个元素逐一进行操作。这表明,通用函数分别处理输入数组的每个元素,生成的结果组成一个新的输出数组。输出数组的大小跟输入数组相同。
三角函数等很多数学运算符合通用函数的定义,例如,计算平方根的sqrt()函数、用来取对数的log()函数和求正弦值的sin()函数。
import numpy as np
x = np.linspace(start=0, stop=np.pi / 2, num=10)
print(x)
# [0. 0.17453293 0.34906585 0.52359878 0.6981317 0.87266463
# 1.04719755 1.22173048 1.3962634 1.57079633]
y = np.sin(x)
print(y)
# [0. 0.17364818 0.34202014 0.5 0.64278761 0.76604444
# 0.8660254 0.93969262 0.98480775 1. ]
z = np.arcsin(y)
print(z)
# [0. 0.17453293 0.34906585 0.52359878 0.6981317 0.87266463
# 1.04719755 1.22173048 1.3962634 1.57079633]
y = np.cos(x)
print(y)
# [1.00000000e+00 9.84807753e-01 9.39692621e-01 8.66025404e-01
# 7.66044443e-01 6.42787610e-01 5.00000000e-01 3.42020143e-01
# 1.73648178e-01 6.12323400e-17]
z = np.arccos(y)
print(z)
# [0. 0.17453293 0.34906585 0.52359878 0.6981317 0.87266463
# 1.04719755 1.22173048 1.3962634 1.57079633]
y = np.tan(x)
print(y)
# [0.00000000e+00 1.76326981e-01 3.63970234e-01 5.77350269e-01
# 8.39099631e-01 1.19175359e+00 1.73205081e+00 2.74747742e+00
# 5.67128182e+00 1.63312394e+16]
z = np.arctan(y)
print(z)
# [0. 0.17453293 0.34906585 0.52359878 0.6981317 0.87266463
# 1.04719755 1.22173048 1.3962634 1.57079633]指数和对数
numpy.exp
numpy.log
numpy.exp2
numpy.log2
numpy.log10
numpy.exp(x, *args, **kwargs)Calculate the exponential of all elements in the input array.numpy.log(x, *args, **kwargs)Natural logarithm, element-wise.numpy.exp2(x, *args, **kwargs)Calculate2**pfor allpin the input array.numpy.log2(x, *args, **kwargs)Base-2 logarithm ofx.numpy.log10(x, *args, **kwargs)Return the base 10 logarithm of the input array, element-wise.
import numpy as np
x = np.arange(1, 5)
print(x)
# [1 2 3 4]
y = np.exp(x)
print(y)
# [ 2.71828183 7.3890561 20.08553692 54.59815003]
z = np.log(y)
print(z)
# [1. 2. 3. 4.]加法函数、乘法函数
numpy.sum
numpy.sum(a[, axis=None, dtype=None, out=None, …])Sum of array elements over a given axis.
通过不同的 axis,numpy 会沿着不同的方向进行操作:如果不设置,那么对所有的元素操作;如果axis=0,则沿着纵轴进行操作;axis=1,则沿着横轴进行操作。但这只是简单的二位数组,如果是多维的呢?可以总结为一句话:设axis=i,则 numpy 沿着第i个下标变化的方向进行操作。
numpy.cumsum
numpy.cumsum(a, axis=None, dtype=None, out=None)Return the cumulative sum of the elements along a given axis.
聚合函数 是指对一组值(比如一个数组)进行操作,返回一个单一值作为结果的函数。因而,求数组所有元素之和的函数就是聚合函数。ndarray类实现了多个这样的函数。
#返回给定轴上的数组元素的总和。
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = np.sum(x)
print(y) # 575
y = np.sum(x, axis=0)
print(y) # [105 110 115 120 125]
y = np.sum(x, axis=1)
print(y) # [ 65 90 115 140 165]#返回给定轴上的数组元素的累加和。
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = np.cumsum(x)
print(y)
# [ 11 23 36 50 65 81 98 116 135 155 176 198 221 245 270 296 323 351
# 380 410 441 473 506 540 575]
y = np.cumsum(x, axis=0)
print(y)
# [[ 11 12 13 14 15]
# [ 27 29 31 33 35]
# [ 48 51 54 57 60]
# [ 74 78 82 86 90]
# [105 110 115 120 125]]
y = np.cumsum(x, axis=1)
print(y)
# [[ 11 23 36 50 65]
# [ 16 33 51 70 90]
# [ 21 43 66 90 115]
# [ 26 53 81 110 140]
# [ 31 63 96 130 165]]numpy.prod
numpy.prod(a[, axis=None, dtype=None, out=None, …])Return the product of array elements over a given axis.
numpy.cumprod
numpy.cumprod(a, axis=None, dtype=None, out=None)Return the cumulative product of elements along a given axis.
#返回给定轴上数组元素的乘积。
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = np.prod(x)
print(y) # 788529152
y = np.prod(x, axis=0)
print(y)
# [2978976 3877632 4972968 6294624 7875000]
y = np.prod(x, axis=1)
print(y)
# [ 360360 1860480 6375600 17100720 38955840]
#返回给定轴上数组元素的累乘。
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = np.cumprod(x)
print(y)
# [ 11 132 1716 24024 360360 5765760
# 98017920 1764322560 -837609728 427674624 391232512 17180672
# 395155456 893796352 870072320 1147043840 905412608 -418250752
# 755630080 1194065920 -1638662144 -897581056 444596224 -2063597568
# 788529152]
y = np.cumprod(x, axis=0)
print(y)
# [[ 11 12 13 14 15]
# [ 176 204 234 266 300]
# [ 3696 4488 5382 6384 7500]
# [ 96096 121176 150696 185136 225000]
# [2978976 3877632 4972968 6294624 7875000]]
y = np.cumprod(x, axis=1)
print(y)
# [[ 11 132 1716 24024 360360]
# [ 16 272 4896 93024 1860480]
# [ 21 462 10626 255024 6375600]
# [ 26 702 19656 570024 17100720]
# [ 31 992 32736 1113024 38955840]]numpy.diff
numpy.diff(a, n=1, axis=-1, prepend=np._NoValue, append=np._NoValue)Calculate the n-th discrete difference along the given axis.- a:输入矩阵
- n:可选,代表要执行几次差值
- axis:默认是最后一个
import numpy as np
A = np.arange(2, 14).reshape((3, 4))
A[1, 1] = 8
print(A)
# [[ 2 3 4 5]
# [ 6 8 8 9]
# [10 11 12 13]]
print(np.diff(A))
# [[1 1 1]
# [2 0 1]
# [1 1 1]]
print(np.diff(A, axis=0))
# [[4 5 4 4]
# [4 3 4 4]]四舍五入
numpy.around
numpy.around(a, decimals=0, out=None)Evenly round to the given number of decimals.
#将数组舍入到给定的小数位数
import numpy as np
x = np.random.rand(3, 3) * 10
print(x)
# [[6.59144457 3.78566113 8.15321227]
# [1.68241475 3.78753332 7.68886328]
# [2.84255822 9.58106727 7.86678037]]
y = np.around(x)
print(y)
# [[ 7. 4. 8.]
# [ 2. 4. 8.]
# [ 3. 10. 8.]]
y = np.around(x, decimals=2)
print(y)
# [[6.59 3.79 8.15]
# [1.68 3.79 7.69]
# [2.84 9.58 7.87]]numpy.ceil
numpy.floor
numpy.ceil(x, *args, **kwargs)Return the ceiling of the input, element-wise.numpy.floor(x, *args, **kwargs)Return the floor of the input, element-wise.
import numpy as np
x = np.random.rand(3, 3) * 10
print(x)
# [[0.67847795 1.33073923 4.53920122]
# [7.55724676 5.88854047 2.65502046]
# [8.67640444 8.80110812 5.97528726]]
y = np.ceil(x)
print(y)
# [[1. 2. 5.]
# [8. 6. 3.]
# [9. 9. 6.]]
y = np.floor(x)
print(y)
# [[0. 1. 4.]
# [7. 5. 2.]
# [8. 8. 5.]]杂项
numpy.clip
numpy.clip(a, a_min, a_max, out=None, **kwargs):Clip (limit) the values in an array.
Given an interval, values outside the interval are clipped to the interval edges. For example, if an interval of [0, 1] is specified, values smaller than 0 become 0, and values larger than 1 become 1.
import numpy as np
x = np.array([[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25],
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35]])
y = np.clip(x, a_min=20, a_max=30)
print(y)
# [[20 20 20 20 20]
# [20 20 20 20 20]
# [21 22 23 24 25]
# [26 27 28 29 30]
# [30 30 30 30 30]]numpy.absolute
numpy.abs
numpy.absolute(x, *args, **kwargs)Calculate the absolute value element-wise.numpy.abs(x, *args, **kwargs)is a shorthand for this function.
import numpy as np
x = np.arange(-5, 5)
print(x)
# [-5 -4 -3 -2 -1 0 1 2 3 4]
y = np.abs(x)
print(y)
# [5 4 3 2 1 0 1 2 3 4]
y = np.absolute(x)
print(y)
# [5 4 3 2 1 0 1 2 3 4]numpy.sign
numpy.sign(x, *args, **kwargs)Returns an element-wise indication of the sign of a number.
x = np.arange(-5, 5)
print(x)
#[-5 -4 -3 -2 -1 0 1 2 3 4]
print(np.sign(x))
#[-1 -1 -1 -1 -1 0 1 1 1 1]函数
np.diff
同轴下, 后一项减去前一项。结果同轴的元素-1.
import numpy as np
a=np.array([1, 6, 7, 8, 12])
diff_x1 = np.diff(a)
print("diff_x1",diff_x1)
# diff_x1 [5 1 1 4]
# [6-1,7-6,8-7,12-8]
b=np.array([[1, 6, 7, 8, 12],[1, 6, 7, 8, 12]])
diff_x2 = np.diff(b)
print("diff_x2",diff_x2)
# diff_x2
# [[5 1 1 4]
# [5 1 1 4]]
c=b.reshape(5,1,2)
print("c: \n", c)
# c:
# [[[ 1 6]]
#
# [[ 7 8]]
#
# [[12 1]]
#
# [[ 6 7]]
#
# [[ 8 12]]]
diff_x3 = np.diff(c)
print("diff_x3 \n",diff_x3)
# diff_x3
# [[[ 5]] [6-1]
#
# [[ 1]] [8-7]
#
# [[-11]] [1-12]
#
# [[ 1]] [7-6]
#
# [[ 4]]] [12-8]np.hstack
将参数元组的元素数组按水平方向进行叠加
import numpy as np
arr1 = np.array([[1,3], [2,4] ])
arr2 = np.array([[1,4], [2,6] ])
res = np.hstack((arr1, arr2))
print (res)
#[[1 3 1 4]
# [2 4 2 6]]
np.logical_not
这是一个逻辑函数,可按元素计算NOT arr的真值。
# input
arr1 = [1, 3, False, 4]
arr2 = [3, 0, True, False]
# output
out_arr1 = np.logical_not(arr1)
out_arr2 = np.logical_not(arr2)
#Output Array 1 : [False False True False]
#Output Array 2 : [False True False True]
arr1 = np.arange(8)
# Applying Condition
print ("Output : \n", arr1/4)
# output
out_arr1 = np.logical_not(arr1/4 == 0)
print ("\n Boolean Output : \n", out_arr1)
#Output :
# [ 0. 0.25 0.5 0.75 1. 1.25 1.5 1.75]
# Boolean Output :
# [False True True True True True True True]np.mean
np.mean(a, # 必须是数组
axis=None,
dtype=None,
out=None,
keepdims=)
mean()函数的功能是求取平均值,经常操作的参数是axis
axis不设置值,对m*n个数求平均值,返回一个实数
axis = 0:压缩行,对各列求均值,返回1*n的矩阵
axis = 1: 压缩列,对各行求均值,返回m*1的矩阵
dtype 精度 来源:Numpy实践 - AI学习 - 阿里云天池 (aliyun.com)
np.diff函数_武科大许志伟的博客-CSDN博客
np.hstack 用法_66565906的博客-CSDN博客_np.hstack
Python numpy.logical_not()用法及代码示例 - 纯净天空 (vimsky.com)
numpy mean()函数 详解_Vic_Hao的博客-CSDN博客_np.mean函数
numpy.split()函数_CodingALife的博客-CSDN博客_numpy split
Python中numpy库unique函数解析_yangyuwen_yang的博客-CSDN博客_numpy unique