代码随想录算法训练营第二天| 977.有序数组的平方、209.长度最小的子数组、59.螺旋矩阵II。

977.有序数组的平方

力扣链接：https://leetcode.cn/problems/squares-of-a-sorted-array/

题目说明：给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

 这题一开始看过去没什么思路，乍一看只能想到把所有数平方了然后排序。但是这样子时间复杂度是O(n^2)，应该有什么简便方法。

看了卡哥的思路之后才茅塞顿开，原来这也可以用双指针法！

class Solution {
public:
	vector sortedSquares(vector& nums) {
		vector result(nums.size(), 0);
		int k = nums.size() - 1;
		int i = 0;
		int j = nums.size() - 1;
		while (i <= j) {
			if (nums[i] * nums[i] < nums[j] * nums[j]) {
				result[k] = nums[j] * nums[j];
				j--;
				k--;
			}
			else {
				result[k] = nums[i] * nums[i];
				i++;
				k--;
			}
		}
		return result;
	}
};

209.长度最小的子数组

力扣链接：https://leetcode.cn/problems/minimum-size-subarray-sum/

题目描述：给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

一开始同样没什么思路，还是只能想到暴力循环。

看了卡哥的思路之后又双叒叕茅塞顿开，学习到了滑动窗口。

class Solution {
public:
	int minSubArrayLen(int target, vector& nums) {
		int i = 0, j = 0;
		int len = 0, shortestLen = nums.size() + 1;
		int sum = 0;
		while (j < nums.size()) {
			sum += nums[j];
			while (sum >= target) {
				len = j - i + 1;
				if (len < shortestLen) {
					shortestLen = len;
				}
				sum -= nums[i];
				i++;
			}
			j++;
		}
		if (shortestLen <= nums.size()) { 
			return shortestLen; 
		}
		else {
			return 0;
		}
	}
};

 不过在写滑动窗口的时候还是遇到了一点坑，包括j溢出等等问题，这里要非常细心。

还有就是审题没审好，没发现题目是和≥S，以至于出现了：

看到这种情况还一脸懵逼，百思不得其解，横算竖算怎么都算不到11以为是题目出错了……

所以同志们审题很重要…… 

59.螺旋矩阵II

力扣链接：https://leetcode.cn/problems/spiral-matrix-ii/

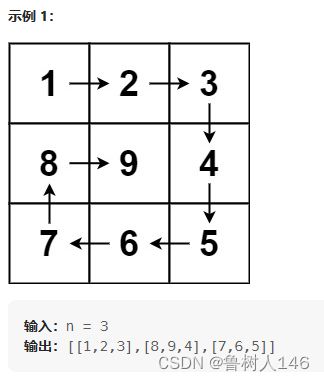
给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

这题我会，四周循环，每次循环不要处理第n-1位。

不过实际写起来还是遇到了一些问题，好在最后还是搞定了。

class Solution {
public:
	vector> generateMatrix(int n) {
		vector> result(n, vector(n, 0));
		int loop = n / 2;
		int count = 1;
		for (int i = 0; i < loop; i++) {
			for (int j = i; j < n - i - 1; j++) {
				result[i][j] = count;
				result[j][n - i - 1] = count + n - 2*i - 1;
				result[n - i - 1][n - j - 1] = count + 2 * (n - 2*i - 1);
				result[n - j - 1][i] = count + 3 * (n - 2*i - 1);
				count++;
			}
			count += 3 * (n - 2 * i - 1);
		}
		if (n % 2) {
			result[n / 2][n / 2] = n * n;
		}
		return result;
	}
};

不过搞定归搞定，这个代码其实是特别难看的，全程不是使用i就是使用j，完全不直观，恐怕过两个月我自己来再看都看不懂我在写什么了……

卡哥提供的代码就非常好，各个关键参数基本都有设定一个变量来记录。