数据结构-队列(链队列与循环队列)

目录

队列的概念及结构

概念

结构

链队列​

初始化QueueInit

销毁QueueDestroy

入队QueuePush

出队QueuePop

队头元素QueueFront​

队尾元素QueueBack

队列长度QueueSize

判断是否为空队列QueueEmpty 

循环队列

概念及结构

循环队列的基本操作​

初始化CQueueInit

销毁CQueueDestroy

入队CQueuePush

​出队CQueuePop

队头元素CQueueFront与队尾元素CQueueBack​

判空CQueueEmpty与判满CQueueFull​

队列长度CQueueSize​

代码

链队列

循环队列

---

队列的概念及结构

概念

   队列也是一种特殊的线性表，其操作受到限制。只允许在队列的一端进行插入数据操作，而在队列的另一端进行删除数据操作。

   在队列中，进行插入数据操作的一端叫做队尾，其操作叫做入队列或者进队列；而进行删除数据操作的一端叫做队头或者队首，其操作叫做出队列或者离队列。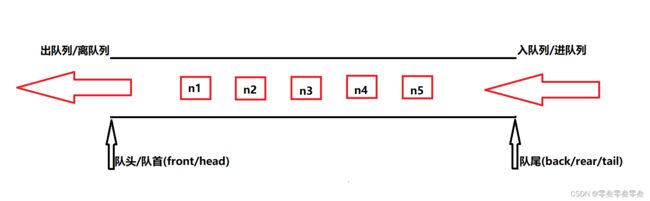

   如上图所示，n1,n2,n3,n4,n5依次从队尾入队，队头元素是n1，队尾元素是n5；而出队只能从另一端队头出，次序依次为n1,n2,n3,n4,n5。这和我们日常生活中的排队相似，最早排队的也是最早离队的，所以队列的特性可以概括为先进先出（First In First Out，FIFO）。

结构

   队列的实现可以选择顺序表与链表，但因为队列是在两端进行操作，如果选择顺序表来实现，在进行出队操作的时候需要挪动数据，效率会比较低。所以队列的实现一般都是选择单链表，在单链表的头部进行出队，单链表的尾部进行入队；为了避免在入队的时候需要找尾结点，我们可以事先保存单链表尾结点的地址来提高效率。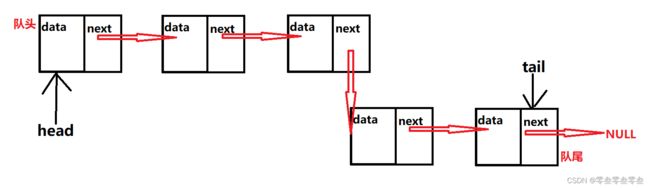

---

链队列

初始化QueueInit

   初始化队列，将队列的头指针与尾指针置空，也就是创建一个空队列。

销毁QueueDestroy

   销毁的操作就是先将非出队的元素释放，再将头指针与尾指针置空。

入队QueuePush

   如果入队时，队列为空需要将头指针与尾指针指向第一个元素；而其他情况就是将尾指针的next改为newNode的地址，再将尾指针指向newNode。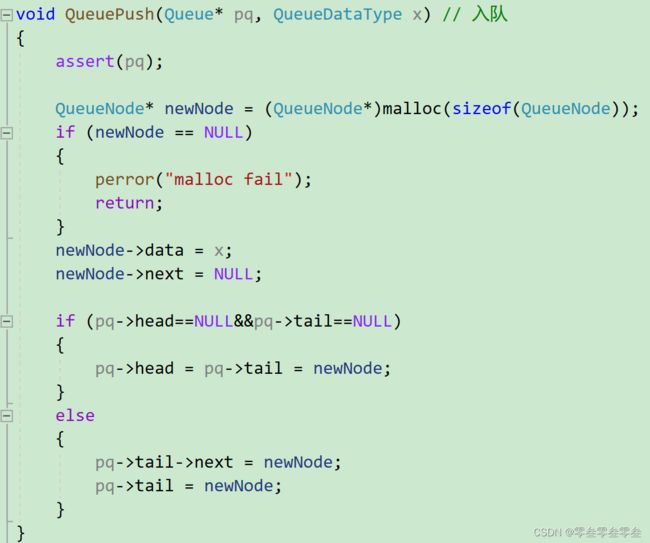

出队QueuePop

   当出队时，队列中只剩下一个元素需要先释放最后一个元素，再将头指针与尾指针置空；其他情况就是先保存队头元素下一个元素的地址，先将头指针指向的队头元素释放，然后将头指针改为事先保存好的元素地址。

队头元素QueueFront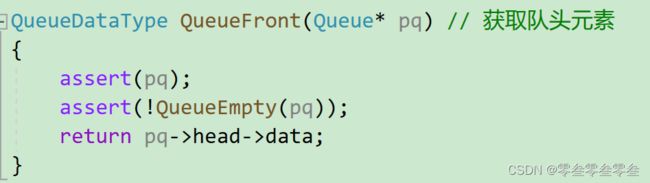

队尾元素QueueBack

队列长度QueueSize

   求队列的长度，就是将单链表遍历一遍。

判断是否为空队列QueueEmpty 

   如果队列为空返回true，不为空返回false。

---

循环队列

概念及结构

   在顺序表实现的队列中，为了避免出队操作需要挪动数据造成的效率低下；我们也可以采用两个下标：一个head记录队头元素的下标，另一个tail记录队尾元素的下一个位置下标。入队时：队列未满，将入队元素赋给tail位置，然后tail下标加一；出队时：队列不空，head下标直接加一，不需要挪动数据。

   但这个顺序表实现的队列有一个缺点，一旦队列满了，我们就不能插入下一个元素，即使队列前面仍有空间；而循环队列的出现就是来解决这个问题的。

   循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队头之后以形成一个循环。它也被称为“环形缓冲器”。使用循环队列，我们能继续使用前面的空间去存储新的值；而且head与tail的下标我们能用除法取余（%）来计算（capacity为开辟元素空间的个数）。

• 入队：tail=（tail+1）%capacity
• 出队：head=（head+1）%capacity
• 队列长度：Size=（capacity+tail-head）%capacity

除了使用mod运算，我们也可以直接判断当head或者tail等于capacity时直接将head或者tail赋值为零；而tail的前一个prev等于-1时，直接将prev赋值为capacity-1即可。

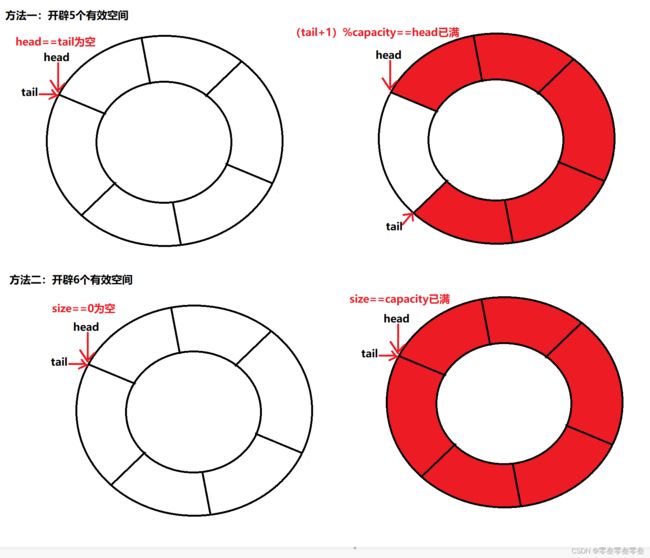
   那么我们该如何判断循环队列的空与满呢？显然循环队列空与满的条件都是head==tail，为了区分循环队列的空与满，有两种常用的处理方式：

• 一：多开辟一个空间，当head在tail的下一个位置则表示队列已满。队列满的条件：（tail+1）%capacity==head；队列空的条件：head==tail。
• 二：增加一个记录队列长度的数据成员size，当size==0时说明队列为空，当size==capacity说明队列已满。

循环队列的基本操作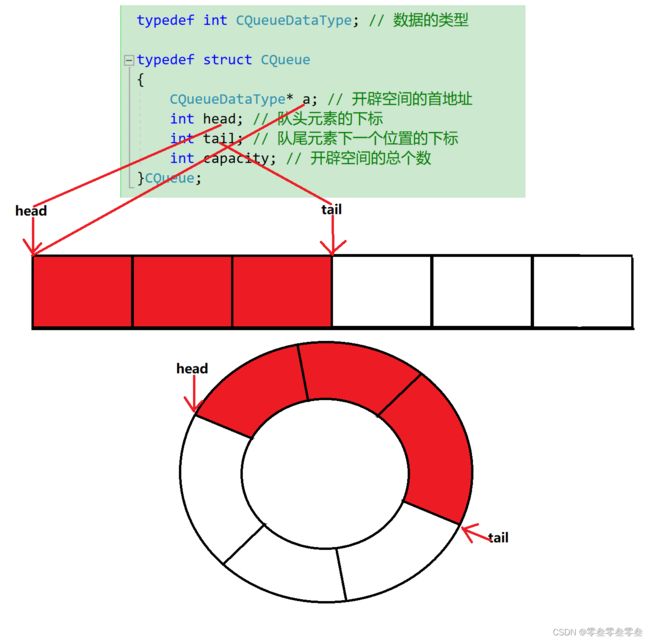

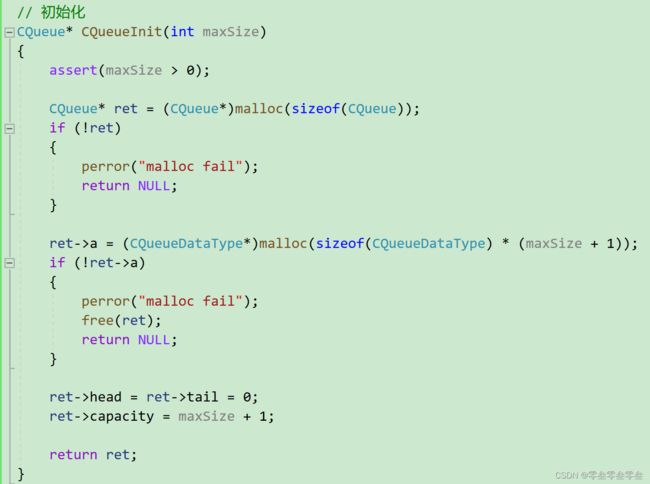
初始化CQueueInit

   先申请队列所需要的数据成员，再申请maxSize个数的空间；因为我们采用的是第一种处理方式所以记得要多开一个空间。

销毁CQueueDestroy

   必须先释放数组的空间，否则数组的空间找不到会出现内存泄漏与越界访问。

入队CQueuePush

   入队成功返回true否则返回false；先将x赋值给tail位置，再将tail下标更新；可以选择tail=（tail+1）%capacity，也可以选择直接判断。

出队CQueuePop

   出队成功返回true否则返回false，将head下标更新；可以选择head=（head+1）%capacity，也可以选择head++，然后判断head是否符合数组下标范围，如果超过将head赋值为零。

队头元素CQueueFront与队尾元素CQueueBack

判空CQueueEmpty与判满CQueueFull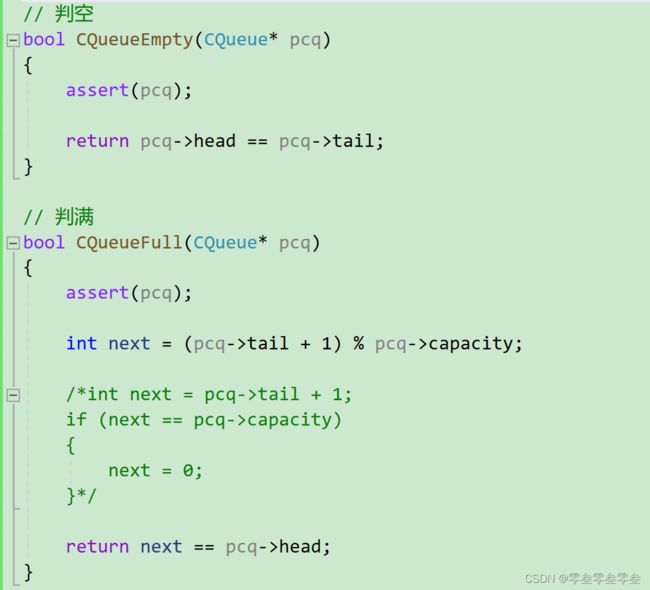

队列长度CQueueSize

---

代码

链队列

// 头文件
typedef int QueueDataType; // 存储的数据类型

typedef struct QueueNode
{
	struct QueueNode* next; // 指向下一个结点
	QueueDataType data; // 存储数据
}QueueNode; 

typedef struct Queue
{
	QueueNode* head; // 头指针
	QueueNode* tail; // 尾指针
}Queue;

void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);

void QueuePush(Queue* pq, QueueDataType x);
void QueuePop(Queue* pq);

QueueDataType QueueFront(Queue* pq);
QueueDataType QueueBack(Queue* pq);

size_t QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);

// 源文件
void QueueInit(Queue* pq) // 初始化
{
	assert(pq);
	pq->head = pq->tail = NULL; // 将头指针与尾指针指向空
}

void QueueDestroy(Queue* pq) // 销毁
{
	assert(pq);
	while (!QueueEmpty(pq)) // 先将非出队的元素释放
	{
		QueuePop(pq);
	}

	/*QueueNode* curr = pq->head;
	while (curr)
	{
		QueueNode* next = curr->next;
		free(curr);
		curr = next;
	}*/

	pq->head = pq->tail = NULL; // 再将头指针与尾指针置空
}

void QueuePush(Queue* pq, QueueDataType x) // 入队
{
	assert(pq);

	QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newNode == NULL)
	{
		perror("malloc fail");
		return;
	}
	newNode->data = x;
	newNode->next = NULL;

	if (pq->head==NULL&&pq->tail==NULL)
	{
		pq->head = pq->tail = newNode;
	}
	else
	{
		pq->tail->next = newNode;
		pq->tail = newNode;
	}
}

void QueuePop(Queue* pq) // 出队
{
	assert(pq);
	assert(!QueueEmpty(pq)); // 队列为空不需要出队

	if (pq->head == pq->tail) // pq->head->next==NULL
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QueueNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
}

QueueDataType QueueFront(Queue* pq) // 获取队头元素
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->head->data;
}

QueueDataType QueueBack(Queue* pq) // 获取队尾元素
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->tail->data;
}

size_t QueueSize(Queue* pq) // 求队列的长度
{
	QueueNode* curr = pq->head;
	size_t size = 0;
	while (curr)
	{
		size++;
		curr = curr->next;
	}

	return size;
}

bool QueueEmpty(Queue* pq) // 判断队列是否为空
{
	return pq->head==NULL&&pq->tail==NULL;
}

循环队列

// 头文件
typedef int CQueueDataType; // 数据的类型

typedef struct CQueue
{
	CQueueDataType* a; // 开辟空间的首地址
	int head; // 队头元素的下标
	int tail; // 队尾元素下一个位置的下标
	int capacity; // 开辟空间的总个数
}CQueue;

// 初始化
CQueue* CQueueInit(int maxSize);
// 销毁
void CQueueDestroy(CQueue* pcq);
// 入队
bool CQueuePush(CQueue* pcq, CQueueDataType x);
// 出队
bool CQueuePop(CQueue* pcq);
// 队头元素
CQueueDataType CQueueFront(CQueue* pcq);
// 队尾元素
CQueueDataType CQueueBack(CQueue* pcq);
// 判空
bool CQueueEmpty(CQueue* pcq);
// 判满
bool CQueueFull(CQueue* pcq);
// 求队列中元素的个数
size_t CQueueSize(CQueue* pcq);

//源文件
// 初始化
CQueue* CQueueInit(int maxSize)
{
	assert(maxSize > 0);

	CQueue* ret = (CQueue*)malloc(sizeof(CQueue));
	if (!ret)
	{
		perror("malloc fail");
		return NULL;
	}

	ret->a = (CQueueDataType*)malloc(sizeof(CQueueDataType) * (maxSize + 1));
	if (!ret->a)
	{
		perror("malloc fail");
		free(ret);
		return NULL;
	}

	ret->head = ret->tail = 0;
	ret->capacity = maxSize + 1;

	return ret;
}

// 销毁
void CQueueDestroy(CQueue* pcq)
{
	assert(pcq);
	free(pcq->a);
	pcq->a = NULL;
	free(pcq);
	pcq = NULL;
}

// 入队
bool CQueuePush(CQueue* pcq, CQueueDataType x)
{
	assert(pcq);

	if(CQueueFull(pcq))
	{
		return false;
	}
	pcq->a[pcq->tail]=x;

	/*pcq->tail = (pcq->tail + 1) % pcq->capacity;*/

	pcq->tail++;
	if (pcq->tail == pcq->capacity)
	{
		pcq->tail = 0;
	}

	return true;
}

// 出队
bool CQueuePop(CQueue* pcq)
{
	assert(pcq);

	if (CQueueEmpty(pcq))
	{
		return false;
	}

	pcq->head = (pcq->head + 1) % pcq->capacity;
	/*pcq->head++;
	if (pcq->head == pcq->capacity)
	{
		pcq->head = 0;
	}*/

	return true;
}

// 队头元素
CQueueDataType CQueueFront(CQueue* pcq)
{
	assert(pcq);
	assert(!CQueueEmpty(pcq));
	return pcq->a[pcq->head];
}

// 队尾元素
CQueueDataType CQueueBack(CQueue* pcq)
{
	assert(pcq);
	assert(!CQueueEmpty(pcq));

	int prev = (pcq->tail - 1 + pcq->capacity) % pcq->capacity;

	/*int prev = pcq->tail-1;

	if (prev == -1)
	{
		prev = pcq->capacity - 1;
	}*/

	return pcq->a[prev];
}

// 判空
bool CQueueEmpty(CQueue* pcq)
{
	assert(pcq);

	return pcq->head == pcq->tail;
}

// 判满
bool CQueueFull(CQueue* pcq)
{
	assert(pcq);

	int next = (pcq->tail + 1) % pcq->capacity;

	/*int next = pcq->tail + 1;
	if (next == pcq->capacity)
	{
		next = 0;
	}*/

	return next == pcq->head;
}

// 求队列中元素的个数
size_t CQueueSize(CQueue* pcq)
{
	assert(pcq);

	return(pcq->tail + pcq->capacity - pcq->head) % pcq->capacity;
}