栈和队列实现原理及实践
栈和队列实现原理及实践
在 数组 中,可以通过索引访问 随机 元素。 但是,某些情况下,可能需要限制处理的顺序。
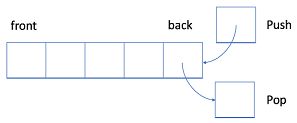
栈:是一个 后入先出(LIFO)数据结构。通常,插入操作在栈中被称作入栈 push ,总是在堆栈的末尾添加一个新元素。删除操作,退栈 pop ,将始终删除最后一个元素。
队列:是一个 先入先出(FIFO) 的数据结构。插入(insert)操作也称作入队(enqueue),新元素始终被添加在队列的末尾。 删除(delete)操作也被称为出队(dequeue),只能移除第一个元素。
栈
栈是一种线性结构,相比数组,栈对应的操作是数组的子集,只能从一端添加元素,也只能从一端取出元素,这一端称为栈顶;
栈是一种后进先出的数据结构 LAST IN FIRST OUT(LIFO)。
在计算机的世界里,栈拥有着不可思议的作用,栈的应用:
- 无处不在的Undo操作(撤销)
- 程序调用使用的系统栈
- 括号匹配-编译器
原理
只允许在栈顶进行操作
- 可使用多种底层数据结构实现,如使用数组实现栈;
- 添加元素时,将元素放置在栈顶,栈的元素数量+1;
- 删除元素时,将栈顶的元素取出,栈的元素数量-1;
时间复杂度分析
ArrayStack
- void push(E) 入栈 O(1) 均摊
- E pop() 出栈 O(1) 均摊
- E peek() 查看栈顶元素 O(1)
- int getSize() 获取栈元素数量 O(1)
- boolean isEmpty() 是否为空 O(1)
队列
队列是一种线性结构,相比数组,队列对应的操作是数组的子集,只能从一端(队尾)添加元素,只能从另一端(队首)取出元素;
队列是一种先进先出的数据结构,First In First Out(FIFO)。
原理
数组队列:
- 入队操作,不断往数组尾部添加元素
- 出队操作,将数组array[0]位置元素取出,将剩余元素全部往前移动一位;array[i] = array[i+1];
固定容量循环队列:
- 定义:
- 存放元素数组为:data,数组长度为:data.length
- 声明3个变量:front指向要出队位置的元素,tail-指向要添加的位置;size-数组中存放元素数量;
- 结论:
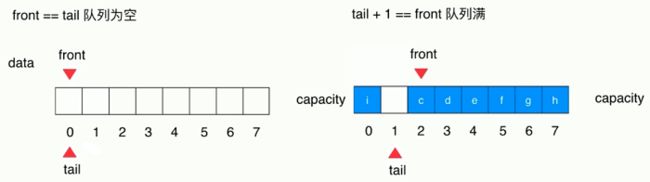
- 当size == 0时,队列为空;
- 当size == data.length,队列已满;
- 队列初始化: front = tail = 0; size= 0; 队列为空;
- 入队:
- 如果size < data.length(否则返回队列已满),当需要入队时,将元素放到tail位置,tail向后移一位;
- 如果当tail已经在数组最后一个位置时,tail重置到0位置;tail = tail == data.length-1 ? 0 : tail + 1;
- 出队:
- 如果size != 0(否则返回队列为空),当需要出队时,将front位置的元素出队,front向后移一位;
- 如果当front已经在数组最后一个位置时,front重置到0位置;front = front == data.length-1 ? 0 : front + 1;
动态容量循环队列:
- 定义
- 存放元素数组为data,数组长度为 data.length,
- 队列容量capacity=data.length-1(浪费1个空间,用于区分队列为空和队列已满两种情况),队列中元素数量size;
- 声明两个变量:front,tail分别指向数组中队首和队尾的位置;
- 当front == tail 时,队列为空;
- 当(tail + 1)%data.length == front时,队列为满;(浪费1个空间,用于区分队列为空和队列已满两种情况;如果不浪费一个空间的情况下,队列为空和为满的情况下front == tail)
- 数组初始设置front=tail=0位置;
- 入队操作,
- 检查队列是否已满,是则对数组进行扩容为原来的2位;resize(2*capacity);
- 将元素放到tail指向的位置,tail = (tail + 1) % data.length;
- 出队操作,
- 将front指向的元素从数组中取出,front = (front + 1) % data.length;
- 检查数组中元素数量是否为数组容量的1/4且数组容量的除2不等0,对数组进行缩容; if(size == capacity/4 && capacity/2 != 0) resize(capacity/2);
- resize数组扩缩容操作,
- 将原数组中元素从 front 开始,i=0,取(front+i)%data.length位置元素,i加1,直到取出size个元素,将旧数组中元素全部放入新数组中;
- for(int i = 0; i < size; i++)newData[i] = data[(i + front) % data.length];
时间复杂度分析
ArrayQueue 数组队列
- void enqueue(E) 往队尾添加元素 O(1) 均摊
- resize()通过均摊复杂度分析为 O(1)
- E dequeue() 取出队首元素 O(n)
- E getFront() 获取队首元素 O(1)
- int getSize() 数组队列元素数量 O(1)
- boolean isEmpty() 判断是否为空 O(1)
LoopQueue 固定容量循环队列
- void enqueue(E) 往队尾添加元素 O(1)
- E dequeue() 取出队首元素 O(1)
- E getFront() 获取队首元素 O(1)
- int getSize() 数组队列元素数量 O(1)
- boolean isEmpty() 判断是否为空 O(1)
LoopQueue 动态容量循环队列
- void enqueue(E) 往队尾添加元素 O(1) 均摊
- resize()通过均摊复杂度分析为 O(1)
- E dequeue() 取出队首元素 O(1) 均摊
- resize()通过均摊复杂度分析为 O(1)
- E getFront() 获取队首元素 O(1)
- int getSize() 数组队列元素数量 O(1)
- boolean isEmpty() 判断是否为空 O(1)
resize() 动态扩缩容
- 时间复杂度为 O(n)
- 通过均摊复杂度分析,将resize()操作均摊到每一个出队或入队的操作中,即相当于每一个出队或入队操作执行两次出队或入队的基本操作,得到resize()操作的均摊时间复杂度为O(1)
- (参见《数组》一文中时间复杂度分析)
实践
- 数组栈
- Leetcode练习-20 Valid Parentheses 匹配括号
- 数组队列
- 固定容量循环队列
- 动态容量循环队列
- Leetcode 102. Binary Tree Level Order Traversal
数组栈
public interface Stack<E> {
/** 入栈 */
void push(E e);
/** 出栈 */
E pop();
/** 查看栈顶元素 */
E peek();
/** 查看栈内元素数量 */
int getSize();
/** 是否为空栈 */
boolean isEmpty();
}
public class ArrayStack<E> implements Stack<E>{
public static final int DEFAULT_CAPACITY = 16;
private Array<E> data;
public ArrayStack(){
this(DEFAULT_CAPACITY);
}
public ArrayStack(int capacity){
data = new DynamicArray<>(capacity);
}
@Override
public void push(E e) {
data.addLast(e);
}
@Override
public E pop() {
return data.removeLast();
}
@Override
public E peek() {
return data.get(data.getSize()-1);
}
@Override
public int getSize() {
return data.getSize();
}
@Override
public boolean isEmpty() {
return data.isEmpty();
}
@Override
public String toString() {
StringBuilder sbr = new StringBuilder("stack size:").append(getSize());
sbr.append(" data: [");
for (int i = 0 ; i < getSize() ; i++){
sbr.append(data.get(i));
if(i != getSize() -1 ){
sbr.append(",");
}
}
sbr.append("] top");
return sbr.toString();
}
}
Leetcode练习-20 Valid Parentheses 匹配括号
/**
给定一个只包括 '(',')','{','}','[',']'的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例 1:
输入: "()"
输出: true
示例2:
输入: "()[]{}"
输出: true
示例3:
输入: "(]"
输出: false
示例4:
输入: "([)]"
输出: false
示例5:
输入: "{[]}"
输出: true
*/
public boolean isValid(String s) {
if(s == null || s.length() < 1 ){
return true;
}
if(s.length() % 2 != 0 ){
return false;
}
Stack<Character> stack = new Stack<>();
for (int i = 0 ; i < s.length() ; i++){
char c = s.charAt(i);
if(c == '(' || c == '[' || c == '{'){
stack.push(c);
}
else {
if(stack.isEmpty()){
return false;
}
char p = stack.pop();
if( ( p == '(' && c != ')' ) || ( p == '[' && c != ']') || ( p == '{' && c != '}') ){
return false;
}
}
}
return stack.isEmpty();
}
数组队列
public interface Queue<E> {
/** 入队 */
void enqueue(E e);
/** 出队 */
E dequeue();
/** 获取队首元素 */
E getFront();
/** 获取队列中元素数量 */
int getSize();
/** 是否为空 */
boolean isEmpty();
}
public class ArrayQueue<E> implements Queue<E>{
public static final int DEFAULT_CAPACITY = 16;
private Array<E> data;
public ArrayQueue(){
this(DEFAULT_CAPACITY);
}
public ArrayQueue(int capacity){
data = new DynamicArray<>(capacity);
}
@Override
public void enqueue(E e) {
data.addLast(e);
}
@Override
public E dequeue() {
return data.removeFirst();
}
@Override
public E getFront() {
return data.get(0);
}
@Override
public int getSize() {
return data.getSize();
}
@Override
public boolean isEmpty() {
return data.isEmpty();
}
@Override
public String toString() {
StringBuilder sbr = new StringBuilder("queue size:").append(getSize()).append(" capacity:").append(data.getCapacity());
sbr.append(" data: front [");
for (int i = 0 ; i < getSize() ; i++){
sbr.append(data.get(i));
if(i != getSize() -1 ){
sbr.append(",");
}
}
sbr.append("] tail");
return sbr.toString();
}
}
固定容量循环队列
public class LoopQueue<E> implements Queue<E>{
public static final int DEFAULT_CAPACITY = 16;
private E[] data;
private int front;
private int tail;
private int size;
public LoopQueue(){
this(DEFAULT_CAPACITY);
}
public LoopQueue(int capacity){
if(capacity < 1){
capacity = DEFAULT_CAPACITY;
}
data = (E[]) new Object[capacity];
}
private boolean isFull(){
return size == data.length;
}
@Override
public void enqueue(E e) {
if(isFull()){
throw new IllegalArgumentException("queue is full!");
}
data[tail] = e;
size++;
tail = (tail + 1) % data.length ;
}
@Override
public E dequeue() {
if(isEmpty()){
throw new IllegalArgumentException("queue is empty!");
}
E e = data[front];
data[front] = null;
size--;
front = (front + 1) % data.length;
return e;
}
@Override
public E getFront() {
if(isEmpty()){
throw new IllegalArgumentException("queue is empty!");
}
return data[front];
}
@Override
public int getSize() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public String toString() {
StringBuilder sbr = new StringBuilder("queue size:").append(getSize()).append(data.length);
sbr.append(" data: front [");
for (int i = 0 ; i < size ; i++){
int index = (front + i) % data.length;
sbr.append(data[index]);
if(i != size -1 ){
sbr.append(",");
}
}
sbr.append("] tail");
return sbr.toString();
}
}
动态容量循环队列
public class DynamicLoopQueue<E> implements Queue<E> {
public static final int DEFAULT_CAPACITY = 16;
private E[] data;
private int front;
private int tail;
private int size;
public DynamicLoopQueue(){
this(DEFAULT_CAPACITY);
}
public DynamicLoopQueue(int capacity){
if(capacity < 1){
capacity = DEFAULT_CAPACITY;
}
// 多留一个空间,用于区分队列空和满的情况
data = (E[])new Object[capacity+1];
}
private boolean isFull(){
return front == (tail + 1) % data.length;
}
private int getCapacity(){
return data.length - 1 ;
}
@Override
public void enqueue(E e) {
if(isFull()){
resize(getCapacity() * 2);
}
data[tail] = e;
tail = (tail +1)%data.length;
size++;
}
@Override
public E dequeue() {
if(isEmpty()){
throw new IllegalArgumentException("queue is empty!");
}
E e = data[front];
data[front] = null;
front = (front + 1) % data.length;
size--;
if(size < (getCapacity() / 4) && (getCapacity() / 2) != 0){
resize(getCapacity()/2);
}
return e;
}
@Override
public E getFront() {
if(isEmpty()){
throw new IllegalArgumentException("queue is empty!");
}
return data[front];
}
@Override
public int getSize() {
return size;
}
@Override
public boolean isEmpty() {
return front == tail;
}
private void resize(int newCapacity) {
E[] newData = (E[])new Object[newCapacity+1];
for (int i = 0 ; i < size ; i++ ){
int index = (front + i)%data.length;
newData[i] = data[index];
}
front = 0 ;
tail = size ;
data = newData;
}
@Override
public String toString() {
StringBuilder sbr = new StringBuilder(String.format("queue size= %d capacity= %d",getSize(),getCapacity()));
sbr.append(" data: front [");
for (int i = 0 ; i < size ; i++){
int index = (front + i) % data.length;
sbr.append(data[index]);
if(i != size -1 ){
sbr.append(",");
}
}
sbr.append("] tail");
return sbr.toString();
}
}
Leetcode 102. Binary Tree Level Order Traversal 二叉树层序遍历
public List<List<Integer>> levelOrder(TreeNode root) {
if(root == null){
return new ArrayList<>();
}
List<List<Integer>> result = new ArrayList<>();
Queue<Node> queue = new DynamicLoopQueue<>();
queue.enqueue(new Node(root,0));
int level = 0 ;
List<Integer> tmpList = new ArrayList<>();
while (!queue.isEmpty()){
Node node = queue.dequeue();
if(node.level != level){
result.add(tmpList);
tmpList = new ArrayList<>();
level = node.level;
}
tmpList.add(node.treeNode.val);
if(node.treeNode.left != null){
queue.enqueue(new Node(node.treeNode.left,node.level+1));
}
if(node.treeNode.right != null){
queue.enqueue(new Node(node.treeNode.right,node.level+1));
}
}
result.add(tmpList);
return result;
}
相关链接
gitee地址:https://gitee.com/chentian114/chen_datastruct_study
github地址:https://github.com/chentian114/data-struct-and-algorithm
CSDN地址:https://blog.csdn.net/chentian114/category_9997109.html
公众号
![]()
参考
Leetcode
刘宇波《玩转数据结构》课程