POJ 2886 Who Gets the Most Candies? 树状数组+二分

一、题目大意

我们有N个孩子，每个人带着一张卡片，一起顺时针围成一个圈来玩游戏，第一回合时，第k个孩子被淘汰，然后他说出他卡片上的数字A，如果A是一个正数，那么下一个回合他左边的第A个孩子被淘汰，如果A是一个负数，那么下一个回合，他右边的第(-A)个孩子被淘汰，如下图所示，即A>0，向着下标增大的方向，A<0，向着下标减小的方向。

其中，第 i (1<=i<=N)回合被淘汰的孩子，可以得到F(i)颗糖果，F(i)代表可以整除 i 的因子的数量（包括1和它本身），最终需要输出 N 个孩子中，得到最多的孩子的名字和他得到的糖果数量，假如说有多个孩子都得到这个糖果数量，输出那个最先被淘汰的。

二、解题思路

首先看这个F(i)代表整除 i 的数量，然后针对输入的 N，我们要找出其中使得 F(i)最大的i，同时如果有多个 i 的F(i)一样，取那个最小的 i。

我们可以定义一个数组F[i]，对于某一个数字 i，只需要枚举 [1,根号i取整] 范围内的数字 j ，然后如果 i % j == 0，F[i]+=2（因为 j 和 i / j 都是整除 i 的因子，所以需要都加上）然后若 j == i / j ，那么F[i]+=1即可，因为两个乘数相等了。

然后我们根据输入的 N，要迅速找到其中 i ∈[1,N]且 F[i]最大的i，那么考虑可先打表，计算好F[i]数组之后，从1到500000循环，定义一个数组optF，其中optF[i]代表 j∈[1,i]时，使得 f[j]最大的j。给optF[0]=0，然后1<=i<=500000循环，如果F[i]>optF[i-1]，则optF[i]=i，否则optF[i]=optF[i-1]，这样可以达到两点，1、对于给定的N，直接用optF[N]可以迅速定位到 j ∈ [1,N]，使F[j]最大的j。2、当F[p]==F[p+k]时，因为时从1循环，以大于为条件，所以当 p <=N且 p+k<=N时，我们会找到满足条件的顺序最靠前的p。

举个例子吧，

1、N∈[1,1]时，最大的因子数是1，N以内最优的数字也是1；

2、N∈[2,3]时，最大的因子数是2，N以内最优的数字是2；

3、N∈[4,5]时，最大的因子数是3，N以内最优的数字是4；

4、N∈[6,11]时，最大的因子数是4，N以内最优的数字是6；

4、N∈[12,23]时，最大的因子数是6，N以内最优的数字是12；

那么来分析下复杂性，计算F数组的值需要的时间复杂性是 O ( N * 根号N），根据F数组，计算optF数组的复杂性是O(N)，对于500000的数据量， O ( N * 根号N）太慢了。那么我们考虑下，hi发现针对 N<=23时，我们只需要记录4个区间的边界和最优的那个F[i]即可。那么对于500000个数字呢？我试了下发现只有35个区间，于是果断写程序把这35个区间的右边界、左边界和最优数字的因子数的打出来的，打表的程序如下。（我发现每次的左边界就是最优数字）

#include 
using namespace std;
typedef pair P;
P tbl[500009];
int f[500009], optF[500009], len;
void initF()
{
    f[0] = 0;
    for (int i = 1; i <= 500000; i++)
    {
        f[i] = 0;
        for (int j = 1; j * j <= i; j++)
        {
            if (i % j == 0)
            {
                f[i] = f[i] + 2;
                if (j * j == i)
                {
                    f[i] = f[i] - 1;
                }
            }
        }
    }
}
void initOptF()
{
    optF[0] = 0;
    for (int i = 1; i <= 500000; i++)
    {
        if (f[i] > f[optF[i - 1]])
        {
            optF[i] = i;
        }
        else
        {
            optF[i] = optF[i - 1];
        }
    }
}
void printTbl()
{
    len = 1;
    tbl[1] = P(1, optF[1]);
    for (int i = 2; i <= 500000; i++)
    {
        if (tbl[len].second == optF[i] && i > tbl[len].first)
        {
            tbl[len].first = i;
        }
        else if (tbl[len].second != optF[i])
        {
            tbl[++len] = P(i, optF[i]);
        }
    }
    for (int i = 1; i <= len; i++)
    {
        printf("%d %d %d\n", tbl[i].first, tbl[i].second, f[tbl[i].second]);
    }
    printf("%d\n", len);
}
int main()
{
    initF();
    initOptF();
    printTbl();
    return 0;
}

这样的话，根据任意的N，找出 i ∈[1,N]，且F[i]最大的 i（存在F[i]和F[i+k]相同时，自动定到F[i]），同时算出F[i]的值，可以直接根据这张表在O(1)时间内完成。

int n_Tbl[] = {1, 3, 5, 11, 23, 35, 47, 59, 119, 179, 239, 359, 719, 839, 1259, 1679, 2519, 5039, 7559, 10079, 15119, 20159, 25199, 27719, 45359, 50399, 55439, 83159, 110879, 166319, 221759, 277199, 332639, 498959, 500000};
int k_Tbl[] = {1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040, 7560, 10080, 15120, 20160, 25200, 27720, 45360, 50400, 55440, 83160, 110880, 166320, 221760, 277200, 332640, 498960};
int f_Tbl[] = {1, 2, 3, 4, 6, 8, 9, 10, 12, 16, 18, 20, 24, 30, 32, 36, 40, 48, 60, 64, 72, 80, 84, 90, 96, 100, 108, 120, 128, 144, 160, 168, 180, 192, 200};

假设，根据N我们找到那个最优数字是optOrder，然后接下来需要考虑的就是，如何找到第 optOrder 个被淘汰的孩子呢？

我的思路是模拟出整个游戏的过程，维护一个树状数组，起初的时候给[1,N]内所有的元素的位置都+1，然后每当第x位置的孩子淘汰的时候，给树状数组update(x,-1)。

使用树状数组+二分查找可以迅速找到当前没有被淘汰的孩子中的第 q 个q∈[1,len]，len为当前内有被淘汰的孩子数量，

1、 L = 0 ,R = n+1

2、mid=(L+R)/2

3、query(mid)（树状数组[1,mid]的和）小于q时，L=mid，否则R=mid

4、L+1>=R时，返回 L+1，L+1就是当前未被淘汰的第q个孩子的下标。

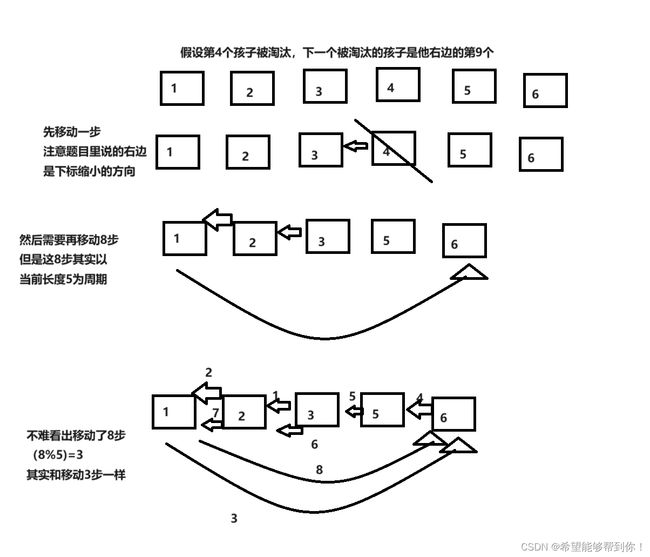
那么来考虑这个游戏的过程，一开始的时候第k个孩子被淘汰，然后根据他卡片上的数字 A 判断下一个孩子，卡片上的数字一定不为0。这里我把这个移动分为两步：

1、先在A方向上移动一步到一个当前没有被淘汰的点

2、然后再移动 A - 1步

然后第二步骤移动时，其实是一个关于当前剩余数量的周期运动，如下图所示。

所以我们把可以把移动的过程优化一下，假设第x个孩子被淘汰，第x个孩子的卡片上数字是A，第x个孩子被淘汰以后，剩余孩子的数量是len

1、先在A方向上移动一步到一个当前没有被淘汰的点

2、然后再移动 (A - 1)% len 步

然后这样的话，就变得简单许多了，我们先利用树状前[1,x]项的和找到下标 x 在被淘汰前在孩子们中的顺序y，之后update(x,-1)代表x被淘汰，同时记录剩余孩子的数量为len，

假设是A是朝着数组下标缩小的方向（题目中的右）

记录方向之后，把A变成正数，便于计算。

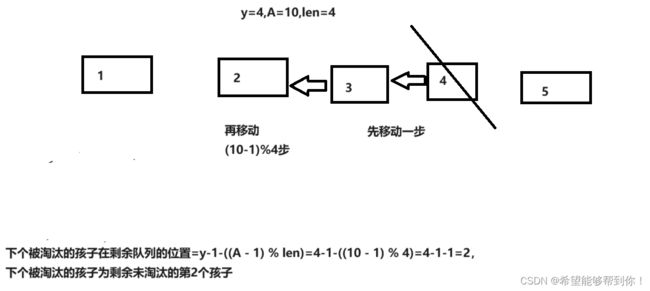
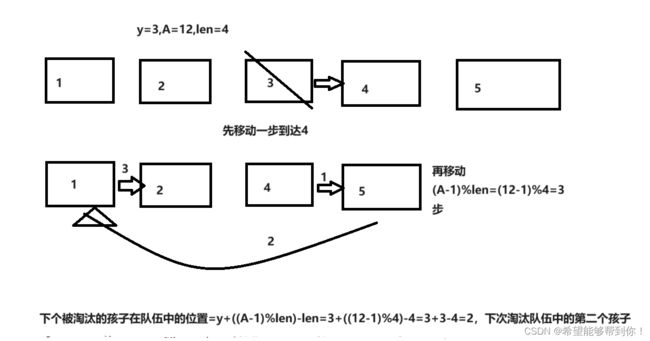
1、被淘汰的孩子位置在y，先挪一步，到 y-1，判断y-1是否大于 (A-1)%len ，如果是，那么下一个被淘汰孩子就是 y - 1 - ((A-1)%len)，如下图所示。

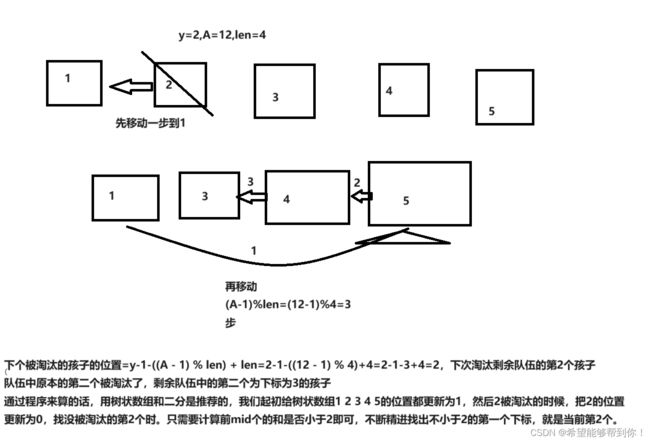
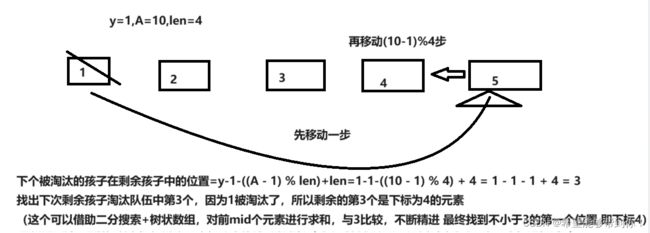
2、如果y-1小于等于 (A-1)%len，那么下一个被淘汰的孩子就是 y - 1 - ((A-1)%len) + len，我给出了2个案例，如下两张图所示。

​​​​​​​

这样就将A向着数组下标缩小方向的所有情况都考虑到了

接下来继续考虑A向着数组下标放大的方向（题目中的左，实际其实是右）

依旧设本次被淘汰的元素在被淘汰前的位置作为y，淘汰掉y之后剩余孩子的数量为len，y手里的数字为A。

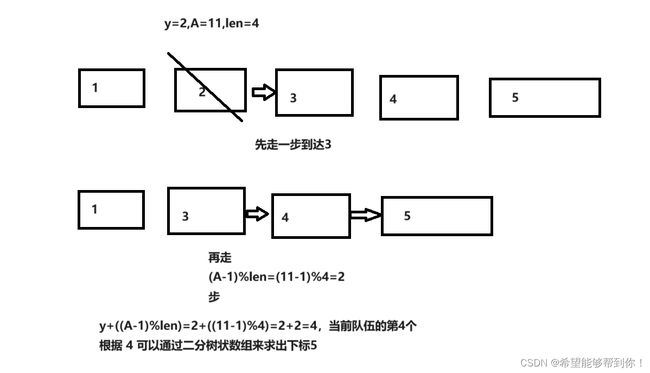
1、首先考虑y加上(A-1)%len小于等于len的情况，这种情况下，下一个被淘汰的位置为 y + ((A-1)%len)，如下图

2、接下来，再来考虑y加上(A-1)%len大于len的情况，这种情况下，可以画图看出下一个被淘汰的位置为y+((A-1)%len) - len，我给出了两个案例，如下两张图所示。

这样就把所有的4种情况考虑完了，知道当前被淘汰的元素下标k后，可知A，也可以通过树状数组计算出它在队伍中的位置y，然后更新树状数组k的位置为-1，剩余长度len自减1，之后通过位置y、偏移A、队伍长度len和上文中的4个if，求出下个被淘汰的孩子在队伍中的位置，然后根据位置对树状数组进行二分，求出下标，更新k为这个下标，继续下一次的循环，这样循环n次，第 i 循环开始时对应的k，就是第i个被淘汰的孩子，这样就可以知道每个孩子被淘汰的顺序了。

之后输出上文中 第optOrder个被淘汰的孩子的名字，和optOrder对应的F值即可。

总结下吧，像这种情况比较多的问题，最好是画下图，我们不需要背下这4个if，只需要能够记得是4种，然后画个图，一个一个找出来就可以

三、代码

#include 
using namespace std;
int n_Tbl[] = {1, 3, 5, 11, 23, 35, 47, 59, 119, 179, 239, 359, 719, 839, 1259, 1679, 2519, 5039, 7559, 10079, 15119, 20159, 25199, 27719, 45359, 50399, 55439, 83159, 110879, 166319, 221759, 277199, 332639, 498959, 500000};
int k_Tbl[] = {1, 2, 4, 6, 12, 24, 36, 48, 60, 120, 180, 240, 360, 720, 840, 1260, 1680, 2520, 5040, 7560, 10080, 15120, 20160, 25200, 27720, 45360, 50400, 55440, 83160, 110880, 166320, 221760, 277200, 332640, 498960};
int f_Tbl[] = {1, 2, 3, 4, 6, 8, 9, 10, 12, 16, 18, 20, 24, 30, 32, 36, 40, 48, 60, 64, 72, 80, 84, 90, 96, 100, 108, 120, 128, 144, 160, 168, 180, 192, 200};
int n_, n, bit[524298], card[500009], order[500009], k;
char name[500009][50];
int optFOrder()
{
    for (int i = 0; i < 35; i++)
    {
        if (n_ <= n_Tbl[i])
        {
            return k_Tbl[i];
        }
    }
    return -1;
}
int f(int num)
{
    for (int i = 0; i < 35; i++)
    {
        if (num <= n_Tbl[i])
        {
            return f_Tbl[i];
        }
    }
    return -1;
}
void input()
{
    for (int i = 1; i <= n_; i++)
    {
        scanf("\n%s %d", &name[i], &card[i]);
    }
}
void init()
{
    n = 1;
    while (n < n_)
    {
        n = n * 2;
    }
    for (int i = 0; i <= n; i++)
    {
        bit[i] = 0;
    }
}
void update(int r, int v)
{
    if (r <= 0)
    {
        return;
    }
    for (int i = r; i <= n; i = i + (i & (-i)))
    {
        bit[i] = bit[i] + v;
    }
}
int query(int r)
{
    int sum = 0;
    for (int i = r; i > 0; i = i - (i & (-i)))
    {
        sum = sum + bit[i];
    }
    return sum;
}
void push()
{
    for (int i = 1; i <= n_; i++)
    {
        update(i, 1);
    }
}
int binarySearch(int num)
{
    int l = 0, r = n + 1;
    while (l + 1 < r)
    {
        int mid = (l + r) / 2;
        if (query(mid) < num)
        {
            l = mid;
        }
        else
        {
            r = mid;
        }
    }
    return (l + 1);
}
int absVal(int num)
{
    if (num < 0)
    {
        return num * (-1);
    }
    else
    {
        return num;
    }
}
void solve()
{
    int len = n_;
    for (int i = 1; i <= n_; i++)
    {
        order[i] = k;
        if (i == n_)
        {
            break;
        }
        len--;
        int currentOrder = query(k);
        update(k, -1);
        bool left = (card[k] < 0);
        card[k] = absVal(card[k]);
        // 默认先挪动一步，挪动一步之后就是len下的周期运动
        card[k]--;
        card[k] = card[k] % len;
        if (left && ((currentOrder - 1) > card[k]))
        {
            k = currentOrder - 1 - card[k];
        }
        else if (left && ((currentOrder - 1) <= card[k]))
        {
            k = currentOrder - 1 - card[k] + len;
        }
        else if (!left && (currentOrder + card[k]) <= len)
        {
            k = currentOrder + card[k];
        }
        else if (!left && (currentOrder + card[k]) > len)
        {
            k = currentOrder + card[k] - len;
        }
        k = binarySearch(k);
    }
}
int main()
{
    while (~scanf("%d%d", &n_, &k))
    {
        input();
        init();
        push();
        solve();
        printf("%s %d\n", name[order[optFOrder()]], f(n_));
    }
    return 0;
}