【算法基础】基础算法(二)--(高精度、前缀和与差分)
一、高精度
当一个数很大,大到 int 无法存下时,我们可以考虑用数组来进行存储,即数组中一个位置存放一位数。
但是对于数组而言,一个数顺序存入数组后,对其相加减是很简单的。但是当需要进位时,还是很麻烦的,因为要将整个数组全都往后移动一位,将最高位的进位位置空出来,这个操作的时间复杂度是 O(n) 。
不过,我们有一种方法可以很好的解决进位这个问题,就是将这个数的个位数存至数组中的第一位(即 a[0] ),最高位存入数组的最后一位(a [n-1])。这样在处理进位时可以直接在数组的最后一位添加即可。最后在输出时逆序输出即可。
1、高精度加法
举个例子:求 9724 + 377 的和。
将两个数分别存入 a 数组和 b 数组中,如下所示:
这样,运算过程就很简单了。将第一个位置进行相加,如果 > 9 就要进一位(这一步可以利用取模来实现)。再将第二个位置的数相加,同时加上前一位的进位,再判断是否 > 9 。以此类推便可求出最终结果。
(1)高精度加法模板
记忆!
// C = A + B, A >= 0, B >= 0
vector add(vector &a,vector &b){
//c为答案
vector c;
//t为进位
int t=0;
for(int i=0;i (2)注意事项
a. 其他写法
如果要处理长度不一致的情况,该怎么做?
可以在循环外先使用条件判断语句来处理这种情况。
可以先判断两个数组的大小,这样在写循环时可以省略一些步骤,但从代码可读性上来讲,还是上面的写法更好理解。
vector add(vector &A, vector &B)
{
if (A.size() < B.size()) return add(B, A);
vector C;
int t = 0;
for (int i = 0; i < A.size(); i ++ )
{
t += A[i];
if (i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
if (t) C.push_back(t);
return C;
} b. 前导 0
如何处理前导 0?
这里所给两个整数不含前导 0,则不需要考虑。处理前导 0 的做法,下面会有详细介绍。
c. 进位
最后需要判断进位是否为 0,如果不为 0,那么不要忘记进 1。为什么是 1,而不可能是其他数字呢?是因为这里是加法,最多只有可能是 9+9,然后再加上一个进位 1,为 19,不会超过这个数,所以之能是 1。
d. 输入输出
需要注意输入时,是从字符串的末尾(即低位: a.size()-1 / b.size()-1 )往前(即 a[0] / b[0] )方向 push_back 输入,那么在 A / B 数组里就会反过来,从低位数在高位下标,高位数在低位下标——>低位数在低位下标,高位数在高位下标,符合我们想要的效果。
e. vector
为什么这里要使用 vector 呢?
- vector 是一个动态数组,可以根据需要动态地分配和释放内存,灵活性较高。在这个场景中,数字相加的结果的位数是不确定的,使用 vector 可以方便地根据实际结果的位数来动态扩展数组的大小。
- vector 提供了丰富的操作函数和方法,如 push_back 用于给末尾添加元素,size 用于获取向量长度,以及通过索引访问元素等。这些方法使得在遍历和操作相加结果的过程中更加方便和高效。
- vector 支持直接返回,可以将结果直接返回给调用者,而不需要手动管理内存或进行额外的拷贝操作。这样可以简化代码,并提高代码的可读性和可维护性。
(3)练习
791. 高精度加法 - AcWing题库
2、高精度减法
减法与加法类似,具体区别有以下有两点:
- 是大的数减小的数还是小的数减大的数,这两种情况的共同点在于它们相减后的绝对值是一样的,所以我们只需要在运算前来判断数的大小即可。
- 也有可能两个数相等或者高位数值相等,那么在相减的过程中会产生 0 ,并且这个 0 是在高位的,在输出时会输出 0 ,那么得要去除这个 0 。若是要求出产生 0 的位置,这个步骤是相对繁琐的。这个时候用数组倒序存数的又一大优势来了,可以直接利用 pop_back() 去除最后的元素(即最高位的元素)。
⚪高精度比大小 (cmp函数)
记忆!
//高精度比大小
bool cmp(vector &A, vector &B) {
if (A.size() != B.size())
return A.size() > B.size();
for (int i = A.size() - 1; i >= 0; i -- )
if (A[i] != B[i])
return A[i] > B[i];
return true;
} (1)高精度减法模板
记忆!
// C = A - B, 满足A >= B, A >= 0, B >= 0
vector sub(vector &A, vector &B)
{
//答案
vector C;
//遍历最大的数
for (int i = 0, t = 0; i < A.size(); i ++ )
{
//t为进位
t = A[i] - t;
//不超过B的范围t=A[i]-B[i]-t;
if (i < B.size()) t -= B[i];
//合二为一,取当前位的答案
C.push_back((t + 10) % 10);
//t<0则t=1
if (t < 0) t = 1;
//t>=0则t=0
else t = 0;
}
//去除前导零
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
} (2)注意事项
a. sub 函数里的 for 循环
因为已经提前确定了函数里的 A.size() >= B.size(); 所以在 for 循环中省略了一个条件判断。
b. 去除前导 0
当数组里的有效数字 > 1 时(答案结果只有一个数字 0,就不需要去除了),且数组末尾(即 back() )为 0 时,利用 while 循环 pop_back 掉这些前导 0。
c. (t + 10)%10
这里会分两种情况:
- t > 0:(t + 10)%10 = t;
- t < 0:t < 0 需要借 1,得到 t+10,由于 t 是负个位数,所以 (t+10)%10 结果为正个位数。
通过 (t + 10)%10 巧妙地将两种情况结合起来。
(3)练习
792. 高精度减法 - AcWing题库
3、高精度乘法
(1)高精度乘低精度
1、高精度乘低精度模板
记忆!
// C = A * b, A >= 0, b >= 0
vector mul(vector &A, int b)
{
//类似于高精度加法
vector C;
//t为进位
int t = 0;
for (int i = 0; i < A.size() || t; i ++ )
{
//不超过A的范围t=t+A[i]*b
if (i < A.size()) t += A[i] * b;
//取当前位的答案
C.push_back(t % 10);
//进位
t /= 10;
}
//去除前导零
while (C.size() > 1 && C.back() == 0) C.pop_back();
return C;
} 2、注意事项
a. 循环条件
在遍历数组 A 的每一位时,需要考虑两个条件:
- 数组A的长度,即 A.size();
- 进位的情况,即当进位不为 0 时,还需要继续进行运算。
b. 去除前导 0
与高精度减法一致,当数组里的有效数字 > 1 时(答案结果只有一个数字 0,就不需要去除了),且数组末尾(即 back() )为 0 时,利用 while 循环 pop_back 掉这些前导 0。这里的去除前导 0 是用来考虑 b 是否等于 0 这种情况的,其他情况不会出现前导 0。
(2)高精度乘高精度
1、高精度乘高精度模板
记忆!
vector mul(vector &A, vector &B) {
vector C(A.size() + B.size()); // 初始化为 0,C的size可以大一点
for (int i = 0; i < A.size(); i++)
for (int j = 0; j < B.size(); j++)
C[i + j] += A[i] * B[j];
for (int i = 0,t = 0; i < C.size(); i++) { // i = C.size() - 1时 t 一定小于 10
t += C[i];
C[i] = t % 10;
t /= 10;
}
while (C.size() > 1 && C.back() == 0) C.pop_back(); // 必须要去前导 0,因为最高位很可能是 0
return C;
} 2、注意事项
a. 进位
为什么 i = C.size() - 1 时,t 一定小于 10?
由于每一位的计算都是将乘法结果加到当前位上,并累积进位值 t,所以在当 i = C.size() - 1时,t 的最大值为乘法结果最高位的数字与之前的进位相加,而乘法结果的每一位数字都 <= 9,进位值 t 也 <= 9。因此,当 i = C.size() - 1 时,进位值 t 一定 < 10。
b. 去除前导 0
与前面一致,当数组里的有效数字 > 1 时(答案结果只有一个数字 0,就不需要去除了),且数组末尾(即 back() )为 0 时,利用 while 循环 pop_back 掉这些前导 0。
(3)练习
793. 高精度乘法 - AcWing题库
4、高精度除法
(1)高精度除低精度
1、高精度除低精度模板
记忆!
// A / b = C ... r, A >= 0, b > 0
vector div(vector &A, int b, int &r)//高精度A,低精度b,余数r
{
vector C;//答案
r = 0;
for (int i = A.size() - 1; i >= 0; i -- )
{
r = r * 10 + A[i];//补全r>=b
C.push_back(r / b);//取当前位的答案
r %= b;//r%b为下一次计算
}
reverse(C.begin(), C.end());//倒序为答案
while (C.size() > 1 && C.back() == 0) C.pop_back();//去除前导零
return C;
} 2、注意事项
a. 去除前导 0
与前面一致,当数组里的有效数字 > 1 时(答案结果只有一个数字 0,就不需要去除了),且数组末尾(即 back() )为 0 时,利用 while 循环 pop_back 掉这些前导 0。
b. 输出顺序
这里通过 reverse 函数将答案倒序为正常顺序。一道题目可能会涉及多种运算,顺序统一更容易处理。
c. 余数
首先将余数 r 初始化为 0,然后从被除数的最高位开始逐位进行除法运算,计算当前位的商并将其添加到结果数组 C 中。具体地,每次对余数 r 进行一次进位运算,将其乘以 10 并加上当前位的数字,得到除数后将其除以 b(低精度除法),即可得到当前位的商,余数则更新为当前余数对除数取模的结果,作为下一次迭代的余数。
d. 除数
注意在 div 函数中不要将 b 习惯性写成 10。
(2)高精度除高精度
⚪高精度比大小 (cmp函数)
记忆!
//高精度比大小
bool cmp(vector &A, vector &B) {
if (A.size() != B.size())
return A.size() > B.size();
for (int i = A.size() - 1; i >= 0; i -- )
if (A[i] != B[i])
return A[i] > B[i];
return true;
} 1、高精度除高精度模板
记忆!
vector div(vector &A, vector &B, vector &r) {
vector C;
if (!cmp(A, B)) {
C.push_back(0);
r.assign(A.begin(), A.end());
return C;
}
int j = B.size();
r.assign(A.end() - j, A.end());
while (j <= A.size()) {
int k = 0;
while (cmp(r, B)) {
r = sub(r, B);
k ++;
}
C.push_back(k);
if (j < A.size())
r.insert(r.begin(), A[A.size() - j - 1]);
if (r.size() > 1 && r.back() == 0)
r.pop_back();
j++;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0)
C.pop_back();
return C;
} 2、注意事项
a. 长度不一致
首先进行比较判断,如果 A < B,则将 0 添加到结果 C 中,得商为 0,并将余数 r 赋值为 A,得 r == A,然后返回结果 C。
b. k 的作用
用于记录每次除法计算中的商。
c. 去除前导 0
这段代码有两处去除前导 0 的地方,其中一处含义与之前一致,另外一处是:如果余数 r 的长度 > 1 且末尾元素为 0,则将末尾的 0 删除,保持余数的最小表示形式,这段代码的目的是去除余数前导的零。
d. 代码解释
vector div(vector &A, vector &B, vector &r) {
vector C;
if (!cmp(A, B)) {
C.push_back(0);
r.assign(A.begin(), A.end());//使得r和A的内容一致
return C;
}
int j = B.size();
r.assign(A.end() - j, A.end());//将A的末尾与除数B长度相同的部分赋值给变量r
while (j <= A.size()) { //循环执行除法运算 直到处理完所有的被除数
int k = 0;//记录每次除法计算中的商
while (cmp(r, B)) {//直到余数r小于除数B为止
r = sub(r, B);//将r减去除数B得到新的余数r
k ++;//每执行一次减法运算,商的个数k就+1
}
C.push_back(k);//将每次除法计算得到的商k添加到C的末尾 用于存储所有的商
if (j < A.size())
r.insert(r.begin(), A[A.size() - j - 1]);//将下一个被除数数字添加到余数r
if (r.size() > 1 && r.back() == 0)
r.pop_back();//去除余数前导的零
j++;
}
reverse(C.begin(), C.end());
while (C.size() > 1 && C.back() == 0)
C.pop_back();
return C;
} (3)练习
794. 高精度除法 - AcWing题库
二、前缀和与差分
1、前缀和
前缀和可以用于快速计算一个序列的区间和,也有很多问题里不是直接用前缀和,但是借用了前缀和的思想。
(1)一维前缀和
预处理出一个前缀和数组后,要求一段区间和可以使用O(1)的时间复杂度快速求出。
【公式】
预处理 : s [ i ] = a [ i ] + a [ i - 1 ]求区间 [ l , r ]: sum = s [ r ] - s [ l - 1 ]" 前缀和数组 " 和 " 原数组 " 可以合二为一
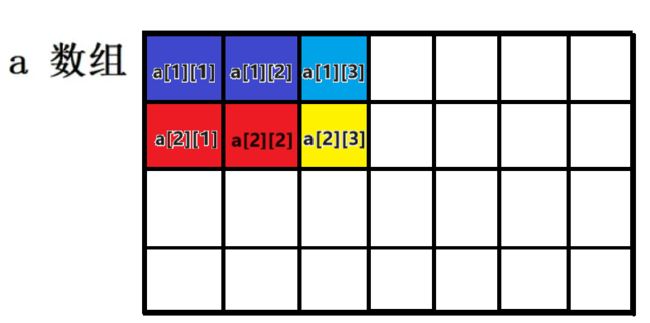
给定一个 a 数组,请求出它的前缀和数组 s :
那么 a 数组的前缀和数组为:
a 数组与 s 数组之间满足:s[i] = a[0] + a[1] + a[2] + … + a[i]
由于我们在计算前缀和时,为了更加方便,我们会将数组下标从 1 开始存入和读取。
所以,我们的 s 前缀和数组为: s[i] = a[1] + a[2] + … + a[i]
如果要求某个区间的和该怎么办?
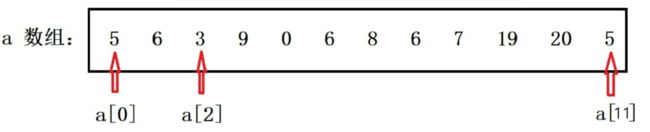
用以上的例子,我们想求 a 数组中下标从 3 到 6 的数值的和。如下图:
用前缀和原理分析可知:a[3] + a[4] + a[5] + a[6] = s[6] - s[2]
【一维前缀和模板】
记忆!
const int N=100010;
int a[N];
int main(){
int n,m;
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)a[i]=a[i-1]+a[i];
scanf("%d",&m);
while(m--){
int l,r;
scanf("%d%d",&l,&r);
printf("%d\n",a[r]-a[l-1]);
}
return 0;
}写法二:
const int N=100010;
int a[N], s[N];
int main(){
int n,m;
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)s[i]=s[i-1]+a[i];
scanf("%d",&m);
while(m--){
int l,r;
scanf("%d%d",&l,&r);
printf("%d\n",s[r]-s[l-1]);
}
return 0;
}【练习】
795. 前缀和 - AcWing题库
(2)二维前缀和
计算矩阵的前缀和: s [ x ][ y ] = s [ x - 1 ][ y ] + s [ x ][ y - 1 ] - s [ x - 1 ][ y - 1 ] + a [ x ][ y ]以 ( x1 , y1 ) 为左上角, ( x2 , y2 ) 为右下角的子矩阵的和为:计算子矩阵的和: s = s [ x2 ][ y2 ] - s [ x1 - 1 ][ y2 ] - s [ x2 ][ y1 - 1 ] + s [ x1 - 1 ][ y1 - 1 ]
思路二:
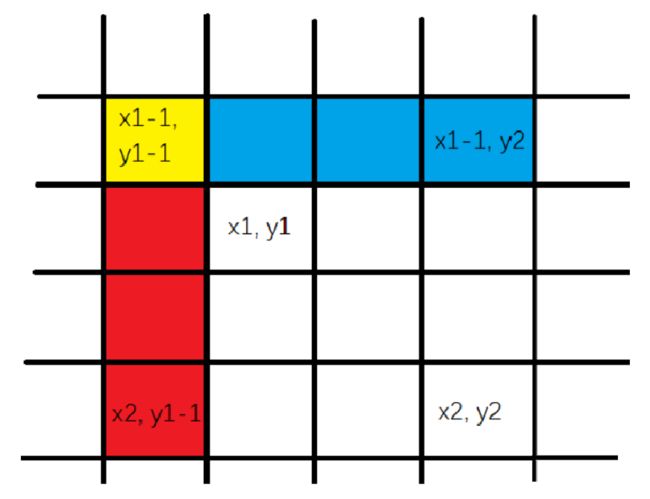
假如我们要求 s[2][3] ,可以根据画图来理解。
s[2][3] 实际上等于下图中绿色区域中数值的和。
我们又可以将这绿色区域划分成以下几种。
我们可以用表达式表示成:s[2][3] = s[2][2] + s[1][3] - s[1][2] + a[2][3]
因为我们在求 s[2][2] 和 s[1][3] 时会求和两次 s[1][2], 所以我们需要再减去一次 s[1][2]。
【二维前缀和模板】
记忆!
int s[1010][1010];
int n,m,q;
int main(){
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&s[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
s[i][j]+=s[i-1][j]+s[i][j-1]-s[i-1][j-1];
while(q--){
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);
}
return 0;
}写法二:
int a[1010][1010], s[1010][1010];
int n,m,q;
int main(){
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&s[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
while(q--){
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
printf("%d\n",s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]);
}
return 0;
}【练习】
796. 子矩阵的和 - AcWing题库
2、差分
差分是前缀和的逆运算,对于一个数组 a ,其差分数组 b 的每一项都是 a[i] 和前一项 a[i−1] 的差。
注意:差分数组和原数组必须分开存放!
- 定义:对于已知有 n 个元素的离线数列 a,我们可以建立记录它每项与前一项差值的差分数组 b:显然,b[1] = a[1] - 0 = a[1]; 对于整数 i ∈ [2,n],我们让 b[i] = a[i] - a[i-1]。
- 简单性质:(1)计算数列各项的值:观察 a[2] = b[1]+b[2] = a[1] + (a[2] - a[1]) = a[2] 可知,数列第 i 项的值是可以用差分数组的前 i 项的和计算的,即 a[i] = b[i] 的前缀和。
(1)一维差分
给区间 [ l , r ] 中的每个数加上 c :b [ l ] += c ,b [ r + 1 ] -= c
【一维差分和模板】
记忆!
using namespace std;
int a[100010],s[100010];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)s[i]=a[i]-a[i-1];// 读入并计算差分数组
while(m--){
int l,r,c;
cin>>l>>r>>c;
s[l]+=c;
s[r+1]-=c;// 在原数组中将区间[l, r]加上c
}
for(int i=1;i<=n;i++){
s[i]+=s[i-1];
cout<(2)二维差分
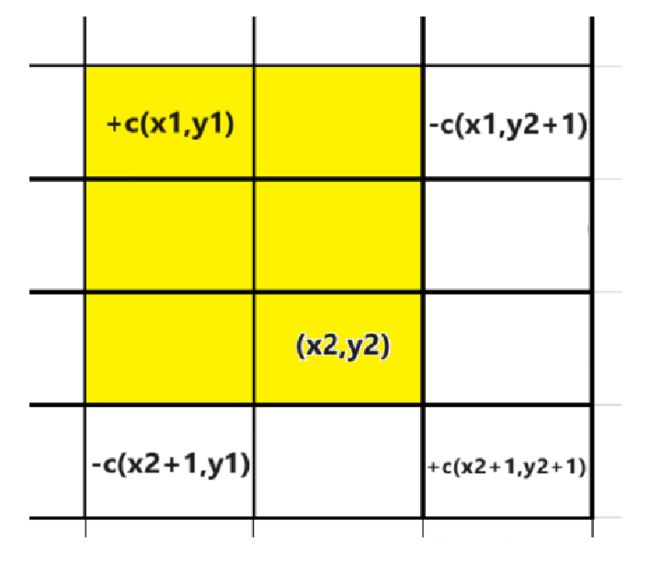
给以 ( x1 , y1 ) 为左上角, ( x2 , y2 ) 为右下角的子矩阵中的所有元素加上 c :b[x1,y1] += c,b[x2+1,y1] -= c,b[x1,y2+1] -= c,b[x2+1,y2+1] += c
二维差分用于在一个矩阵里,快速里把矩阵的一个子矩阵加上一个固定的数。也是直接来修改差分矩阵。试想只要在差分矩阵的(x1,y1) 位置加上 c,那么以它为左上角,所有后面的元素就都加上了 c。要让(x2,y2) 的右边和下边的元素不受影响,由容斥原理可以知道,只要在(x2+1,y1) 和(x1,y2+1) 位置减去 c,再从(x2+1,y2+1) 位置加回 c 就可以了。
【二维差分模板】
记忆!
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
int n, m, q;
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> a[i][j];
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
insert(i, j, i, j, a[i][j]); //构建差分数组
}
}
while (q--)
{
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c);//加c
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; //二维前缀和
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
printf("%d ", b[i][j]);
}
printf("\n");
}
return 0;
}