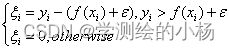基于随机森林算法的森林生物量反演【Matlab Python】
一、意义以及技术路线
估算森林生物量的方法大致可归为以下两种 :一是传统估算方法,大多是采用抽样方法获取野外调查数据估算森林生物量,这种方法往往需要较多的人力物力来完成,并且获取的数据不具有空间连续性特征,无法反映环境因子对估算结果的影响;二是遥感技术估算方法,遥感影像波段具有空间连续性特征,且具有宏观、快速以及可重复等特点,为研究森林生物量及其空间分布提供了必要条件,使得估算结果不仅接近实际,而且可提供直观的森林生物量空间分布信息。
本次使用的路线是后者,遥感技术估算方法,利用LandSat-8卫星观测的数据,使用各种算法使用各波段对生物量构建拟合模型并训练,得到拟合效果较好的模型,反演森林地上生物量(AGB)。
二、 变量提取
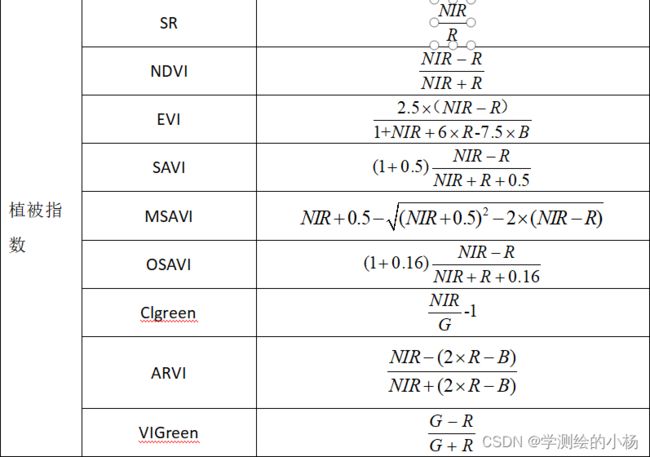
使用ENVI根据下列植被指数计算公式使用Band Math公式计算出五个所选指数,这里选取的五个植被指数分别为ARVI、NDVI、SR、OSAVI和VIGreen五个指数,得到了五幅影像,如下所示。
这次选择ARVI、NDVI、OSAVI、SR和VIGreen植被指数作为参数反演。
使用ENVI软件对遥感图像做纹理特征计算,计算其Mean、Variance、Homogeneity、Contrast、Dissimilarity、Entropy、Second Moment以及Correlation,得到八幅图像。
 Mean
Mean
 Homogeneity
Homogeneity
在这里只展示两幅图像。
三、样点提取
使用Matlab对预处理好的遥感影像数据、纹理数据和AGB实测值选取相应的随机同名像点,本次选取了556个点构成模型训练的训练集与验证集。
clear;
AGB_data=readgeoraster("AGB_lidarplots.tif");
ARVI_data=readgeoraster("ARVI.tif");
VIGreen_data=readgeoraster("VIGreen.tif");
NDVI_data=readgeoraster("NDVI.tif");
SR_data=readgeoraster("SR.tif");
OSAVI_data=readgeoraster("OSAVI.tif");
Multi_data=readgeoraster("Multispec_ref_layer_stack_clip_corre_allstudyarea_resam_AGB.tif");
Swir1=Multi_data(:,:,2);
Nir=Multi_data(:,:,3);
Red=Multi_data(:,:,4);
Green=Multi_data(:,:,5);
Blue=Multi_data(:,:,6);
Coastal=Multi_data(:,:,7);
texture_data=readgeoraster("texture_NIR.tif");
Mean=texture_data(:,:,1);
Variance=texture_data(:,:,2);
Homogeneity=texture_data(:,:,3);
Contrast=texture_data(:,:,4);
Dissimilarity=texture_data(:,:,5);
Entropy=texture_data(:,:,6);
SecondMoment=texture_data(:,:,7);
Correlation=texture_data(:,:,8);
x=randi(266,1,1000);
y=randi(400,1,1000);
AGB_selected=zeros(1,1000);
SWIR1_selected=zeros(1,1000);
NIR_selected=zeros(1,1000);
RED_selected=zeros(1,1000);
GREEN_selected=zeros(1,1000);
Blue_selected=zeros(1,1000);
COASTAL_selected=zeros(1,1000);
NDVI_selected=zeros(1,1000);
SR_selected=zeros(1,1000);
OSAVI_selected=zeros(1,1000);
ARVI_selected=zeros(1,1000);
VIGreen_selected=zeros(1,1000);
MEAN_selected=zeros(1,1000);
Variance_selected=zeros(1,1000);
Homogeneity_selected=zeros(1,1000);
Contrast_selected=zeros(1,1000);
Dissimularity_selected=zeros(1,1000);
Entropy_selected=zeros(1,1000);
SecondMoment_selected=zeros(1,1000);
Correlation_selected=zeros(1,1000);
for i=1:size(x,2)
xi=x(1,i);
yi=y(1,i);
if xi==0 || yi==0
xi=1;
yi=1;
end
AGB_selected(1,i)=AGB_data(xi,yi);
SWIR1_selected(1,i)=Swir1(xi,yi);
NIR_selected(1,i)=Nir(xi,yi);
RED_selected(1,i)=Red(xi,yi);
GREEN_selected(1,i)=Green(xi,yi);
Blue_selected(1,i)=Blue(xi,yi);
COASTAL_selected(1,i)=Coastal(xi,yi);
NDVI_selected(1,i)=NDVI_data(xi,yi);
SR_selected(1,i)=SR_data(xi,yi);
OSAVI_selected(1,i)=OSAVI_data(xi,yi);
ARVI_selected(1,i)=ARVI_data(xi,yi);
VIGreen_selected(1,i)=VIGreen_data(xi,yi);
MEAN_selected(1,i)=Mean(xi,yi);
Variance_selected(1,i)=Variance(xi,yi);
Homogeneity_selected(1,i)=Homogeneity(xi,yi);
Contrast_selected(1,i)=Contrast(xi,yi);
Dissimularity_selected(1,i)=Dissimilarity(xi,yi);
Entropy_selected(1,i)=Entropy(xi,yi);
SecondMoment_selected(1,i)=SecondMoment(xi,yi);
Correlation_selected(1,i)=Correlation(xi,yi);
end
%输出到excel中
data=cell(1000,20);
%title={'AGB','SWIR1','NIR','RED',"GREEN",'Blue','COASTAL','NDVI','SR','OSAVI','ARVI','VIGreen','MEAN','Variance','Homogeneity','Contrast','Dissimularity','Entropy','Second Moment','Correlation'};
result=[AGB_selected;SWIR1_selected;NIR_selected;RED_selected;GREEN_selected;Blue_selected;COASTAL_selected;NDVI_selected;SR_selected;OSAVI_selected;ARVI_selected;VIGreen_selected;MEAN_selected;Variance_selected;Homogeneity_selected;Contrast_selected;Dissimularity_selected;Entropy_selected; SecondMoment_selected;Correlation_selected];
result=result';
xlswrite('data.xlsx',result)四、变量筛选
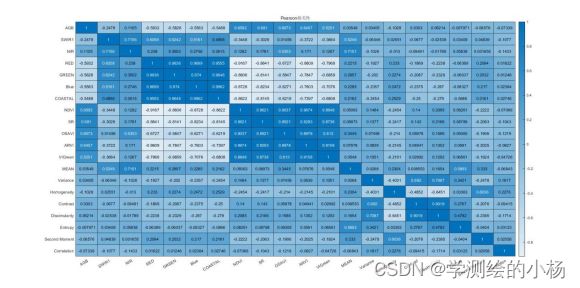
对所有的数据进行变量筛选以确定在模型拟合中所使用的变量,可以使用相关性分析、重要性排序以及前向/后向筛选等方法,本次综合设计中使用的是相关性分析中的Pearson相关性指数判定AGB和各变量之间的相关性。
clear;
%读取excel数据
[num]=readtable("筛选后.xls");
AGB=table2array(num(:,1));
SWIR1=table2array(num(:,2));
NIR=table2array(num(:,3));
RED=table2array(num(:,4));
Green=table2array(num(:,5));
Blue=table2array(num(:,6));
Coastal=table2array(num(:,7));
NDVI=table2array(num(:,8));
SR=table2array(num(:,9));
OSAVI=table2array(num(:,10));
ARVI=table2array(num(:,11));
VIGreen=table2array(num(:,12));
Mean=table2array(num(:,13));
Variance=table2array(num(:,14));
Homogeneity=table2array(num(:,15));
Contrast=table2array(num(:,16));
Dissimularity=table2array(num(:,17));
Entropy=table2array(num(:,18));
SecondMoment=table2array(num(:,19));
Correlation=table2array(num(:,20));
data=[AGB,SWIR1,NIR,RED,Green,Blue,Coastal,NDVI,SR,OSAVI,ARVI,VIGreen,Mean,Variance,Homogeneity,Contrast,Dissimularity,Entropy,SecondMoment,Correlation];
data1=[SR,NDVI,OSAVI,ARVI,VIGreen];%自变量准备
[rho,pval]=corr(data,'type','Pearson');
string_name={'AGB','SWIR1','NIR','RED',"GREEN",'Blue','COASTAL','NDVI','SR','OSAVI','ARVI','VIGreen','MEAN','Variance','Homogeneity','Contrast','Dissimularity','Entropy','Second Moment','Correlation'};
x_values=string_name;
y_values=string_name;
h=heatmap(x_values,y_values,rho);
h.Title="Pearson相关性";
% colormap summer
% size(pval)
% h1=heatmap(x_values,y_values,pval);
% h1.Title="显著性水平";
% colormap summer由上图可知,NDVI、SR、OSAVI、ARVI、VIGreen与AGB之间的相关性相较于其他变量更强(Pearson相关性指数约0.6左右),所以选取以上五个变量作为模型输入自变量进行训练。
五、预测模型(随机森林算法 偏最小二乘 SVR支持向量回归)
5.1偏最小二乘算法
偏最小二乘回归(PLSR)是一种线性回归算法。它是一种基于主成分分析的多元统计分析方法,可以用于处理高维数据集中的多个自变量和一个或多个因变量之间的线性关系。PLSR算法通过将自变量和因变量投影到一个新的地位空间,从而降低数据集的维度,并且可以解决自变量之间存在多重共线型的问题。其目的是最小化预测误差的平方和,从而找到最佳的预测模型。
PLSR算法的主要步骤包括:
- 选择投影方向
- 计算投影系数
- 对投影后的变量进行回归分析
- 对回归结果进行交叉验证
- 选择最佳预测模型
代码如下:
%训练集和验证集数据个数分别为
VerifySize=round(size(AGB,1)/3);
TrainSize=size(AGB,1)-VerifySize;
input=data1(1:TrainSize,:);%训练输入值(自变量)
predict_input=data1(TrainSize:end,:);%验证输入值(自变量)
output=AGB(1:TrainSize,:);%训练输出值(因变量)
predict_output=AGB(TrainSize:end,:);%验证输出值(因变量)
%偏最小二乘
var=[input,output];
mu=mean(var);sig=std(var); %求均值和标准差
rr=corrcoef(var); %求相关系数矩阵
ab=zscore(var); %数据标准化
a=ab(:,1:5); %提出标准化后的自变量数据
b=ab(:,6); %提出标准化后的因变量数据
%% 判断提出成分对的个数
[XL,YL,XS,YS,BETA,PCTVAR,MSE,stats] =plsregress(a,b);
xw=a\XS; %求自变量提出成分的系数,每列对应一个成分,这里xw等于stats.W
yw=b\YS; %求因变量提出成分的系数
a_0=PCTVAR(1,:);b_0=PCTVAR(2,:);% 自变量和因变量提出成分的贡献率
a_1=cumsum(a_0);b_1=cumsum(b_0);% 计算累计贡献率
i=1;%赋初始值
while ((a_1(i)<0.999)&(a_0(i)>0.001)&(b_1(i)<0.999)&(b_0(i)>0.001)) % 提取主成分的条件
i=i+1;
end
ncomp=i;% 选取的主成分对的个数
fprintf('%d对成分分别为:\n',ncomp);% 打印主成分的信息
for i=1:ncomp
fprintf('第%d对成分:\n',i);
fprintf('u%d',i);
for k=1:size(a,2)%此处为变量x的个数
fprintf('+(%fx_%d)',xw(k,i),k);
end
fprintf('\n');
fprintf('v%d=',i);
for k=1:size(b,2)%此处为变量y的个数
fprintf('+(%fy_%d)',yw(k,i),k);
end
fprintf('\n');
end
%% 确定主成分后的回归分析
[XL2,YL2,XS2,YS2,BETA2,PCTVAR2,MSE2,stats2] =plsregress(a,b,ncomp);
n=size(a,2); m=size(b,2);%n是自变量的个数,m是因变量的个数
beta3(1,:)=mu(n+1:end)-mu(1:n)./sig(1:n)*BETA2([2:end],:).*sig(n+1:end); %原始数据回归方程的常数项
beta3([2:n+1],:)=(1./sig(1:n))'*sig(n+1:end).*BETA2([2:end],:); %计算原始变量x1,...,xn的系数,每一列是一个回归方程
fprintf('最后得出如下回归方程:\n')
for i=1:size(b,2)%此处为变量y的个数
fprintf('y%d=%f',i,beta3(1,i));
for j=1:size(a,2)%此处为变量x的个数
fprintf('+(%f*x%d)',beta3(j+1,i),j);
end
fprintf('\n');
end
%% 求预测值
y1 = repmat(beta3(1,:),[size(predict_input,1),1])+predict_input(:,[1:n])*beta3([2:end],:); %求y1,..,ym的预测值
y0 = predict_output(:,end-size(y1,2)+1:end); % 真实值
abs(y1-y0);
%%求整体预测值(精度评定)
y_all=repmat(beta3(1,:),[size(data1,1),1])+data1(:,[1:n])*beta3([2:end],:);
y_real=AGB(:,end-size(y1,2)+1:end);
abs(y_all-y_real);
RMSE=sqrt(sum((y_all-y_real).*(y_all-y_real))/size(data1,1));
R2=1-sum((y_all-y_real).^2)/sum((y_real-mean(y_real)).^2);
y2=predict_output;
y3 = repmat(beta3(1,:),[size(predict_input,1),1])+predict_input(:,[1:n])*beta3([2:end],:);
plotregression(y2,y3)
ylabel("AGB预测值(kg/ha)")
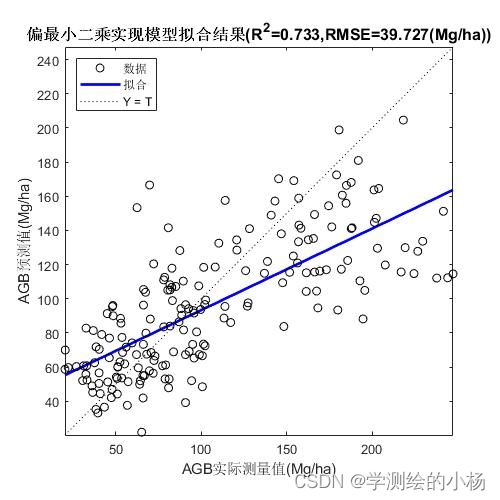
xlabel("AGB实际测量值(kg/ha)")
title("偏最小二乘实现模型拟合结果(R=0.73291,RMSE=39.7270)")结果图如下:
5.2RF-随机森林算法
决策树是比较经典的机器学习算法,可以用来处理分类问题和回归问题。同时也是集成学习中弱学习器经常选择的机器学习算法。如RF,GBDT。
决策树是一种树型结构,每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。决策树是一种基于if-then-else规则的有监督机器学习算法。
决策树学习的算法通常是一个递归地选择最优特征,并根据该特征对训练数据进行分割,使得各个子数据集有一个最好的分类的过程。这一过程对应着对特征空间的划分,也对应着决策树的构建。随机森林(RF)
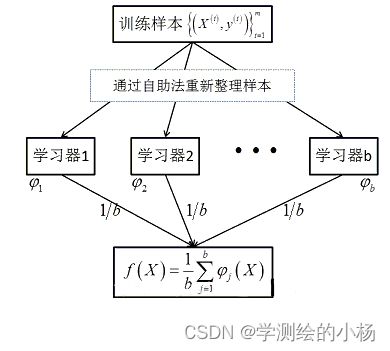
随机森林(RF)其实就是多棵决策树。通过对样本重新采样的方法得到不同的训练样本集,在这些新的训练样本集上分别训练学习器,最终合并每一个学习器的结果,作为最终的学习结果,其中,每个样本的权重是一样的。如下图:
其中,在该方法中,b个学习器之间彼此是相互独立的,这样的特点使该方法更容易并行。自助法即Bootstrap方法进行随机有放回地抽样。学习器即为决策树DT。
算法步骤
每棵树按照如下规则生成:
(1)如果训练集的大小为N,对于每棵树而言,随机有放回地从训练集中抽取N个训练样本,作为该树的训练集。(每棵树训练集不同,而且包含重复样本)
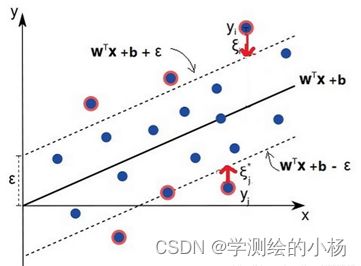
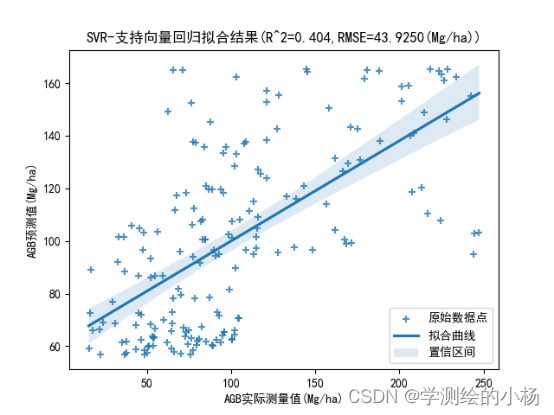
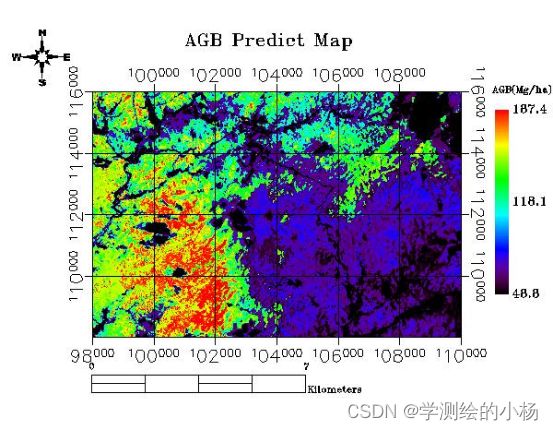
(2)如果每个样本的特征维度为M,指定一个常数m< (3)每棵树都是尽最大程度生长,并且没有剪枝过程。(建立大量决策树,形成森林) 随机:样本随机、特征随机(保证不容易陷入过拟合) 分类问题:对于测试样本,森林中每棵决策树会给出最终类别,最后综合考虑每一棵树输出,投票决定。 其中,在该方法中,b个学习器之间彼此是相互独立的,这样的特点使该方法更容易并行。自助法即Bootstrap方法进行随机有放回地抽样。学习器即为决策树DT。 每棵树按照如下规则生成: (1)如果训练集的大小为N,对于每棵树而言,随机有放回地从训练集中抽取N个训练样本,作为该树的训练集。(每棵树训练集不同,而且包含重复样本) (2)如果每个样本的特征维度为M,指定一个常数m< (3)每棵树都是尽最大程度生长,并且没有剪枝过程。(建立大量决策树,形成森林) 随机:样本随机、特征随机(保证不容易陷入过拟合) 分类问题:对于测试样本,森林中每棵决策树会给出最终类别,最后综合考虑每一棵树输出,投票决定。 由图像可知 当Tree的数目位于166附近时,MSE减少的趋势缓慢,且当叶子数为20时,MSE的值最小。所以该模型的树的数量为166,叶子数为20。 使用训练集对模型进行训练,输入自变量,计算预测值,判定当RMSE小于35时停止训练。 结果如下: 代码如下: 在线性函数的两侧创造了一个“间隔带”,而这个“间隔带”的间距为ϵ(这个值常是根据经验而给定的),对所有落入到间隔带内的样本不计算损失,也就是只有支持向量才会对其函数模型产生影响,最后通过最小化总损失和最大化间隔来得出优化后的模型。对于非线性的模型,与SVM一样使用核函数(kernel function)映射到特征空间,然后再进行回归。 公式化表示 SVR模型在使用中和传统的一般线性回归模型也有一些的区别,其区别主要体现在SVR模型中当且仅当和f(x)和y之间的差距的绝对值大于ϵ时才计算损失,而一般的线性模型中只要f(x)和y不相等就计算损失。 两种模型的优化方法不同,SVR模型中通过最大化间隔带的宽度和最小化损失来优化模型,而在一般的线性回归模型中是通过梯度下降后的平均值来优化模型。 划分好数据集后,设置好惩罚参数以及ε宽度值,进行模型训练你和,得到的结果为下图。 代码如下: 综合评估可得: 随机森林 偏最小二乘 SVR向量回归 R^2 0.744 0.732 0.404 RMSE(Mg/ha) 28.895 39.727 43.925 综上所述,RF-随机森林拟合算法效果最好,其判定系数最接近1且RMSE值最小,则使用RF-随机森林拟合算法进行拟合。 使用envi绘图得到结果:
%RF随机森林
clc;
clear;
[num]=readtable("筛选后.xls");
AGB=table2array(num(:,1));
NDVI=table2array(num(:,8));
SR=table2array(num(:,9));
OSAVI=table2array(num(:,10));
ARVI=table2array(num(:,11));
VIGreen=table2array(num(:,12));
data1=[SR,NDVI,OSAVI,ARVI,VIGreen];%自变量准备
%训练集
input=data1(:,:);%训练输入值(自变量)
output=AGB(:,:);%训练输出值(因变量)
%判断RF算法的叶子数和决策树的数目
for RFOptimizationNum=1:5
RFLeaf=[5,10,20,50,100,200,500];
col='rgbcmyk';
figure('Name','RF Leaves and Trees');
for i=1:length(RFLeaf)
RFModel=TreeBagger(2000,data1,AGB,'Method','R','OOBPrediction','On','MinLeafSize',RFLeaf(i));
plot(oobError(RFModel),col(i));
hold on
end
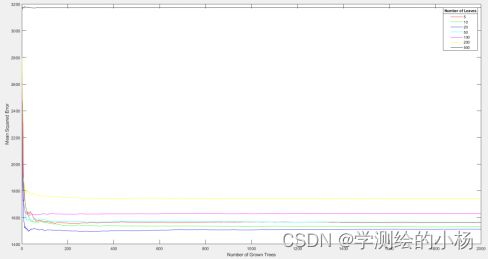
xlabel('Number of Grown Trees');
ylabel('Mean Squared Error') ;
LeafTreelgd=legend({'5' '10' '20' '50' '100' '200' '500'},'Location','NorthEast');
title(LeafTreelgd,'Number of Leaves');
hold off;
disp(RFOptimizationNum);
end
%由图像可知 当Tree的数目位于166附近时,MSE减少的趋势缓慢,且当叶子数为20时,MSE的值最小
RFRMSEMatrix=[];
RFrAllMatrix=[];
RFRunNumSet=50000;
for RFCycleRun=1:RFRunNumSet
% 训练集数据划分
RandomNumber=(randperm(length(output),floor(length(output)/3)))';
TrainYield=output;
TestYield=zeros(length(RandomNumber),1);
TrainVARI=input;
TestVARI=zeros(length(RandomNumber),size(TrainVARI,2));
for i=1:length(RandomNumber)
m=RandomNumber(i,1);
TestYield(i,1)=TrainYield(m,1);
TestVARI(i,:)=TrainVARI(m,:);
TrainYield(m,1)=0;
TrainVARI(m,:)=0;
end
TrainYield(all(TrainYield==0,2),:)=[];
TrainVARI(all(TrainVARI==0,2),:)=[];
%% RF
nTree=166;
nLeaf=20;
RFModel=TreeBagger(nTree,TrainVARI,TrainYield,...
'Method','regression','OOBPredictorImportance','on', 'MinLeafSize',nLeaf);
[RFPredictYield,RFPredictConfidenceInterval]=predict(RFModel,TestVARI);
%RF模型准确度判断
RFRMSE=sqrt(sum(sum((RFPredictYield-TestYield).^2))/size(TestYield,1));
RFrMatrix=corrcoef(RFPredictYield,TestYield);
RFr=RFrMatrix(1,2);
RFRMSEMatrix=[RFRMSEMatrix,RFRMSE];
RFrAllMatrix=[RFrAllMatrix,RFr];
if RFRMSE<34
disp(RFRMSE);
break;
end
disp(RFRMSE);
disp(RFCycleRun);
end
% RF模型存储
RFModelSavePath='E:\微信存储位置\WeChat Files\wxid_xjealsgnaqio21\FileStorage\File\2023-06\海测综合设计-2020级\海测综合设计-2020级\生物量反演\data\matlab';
save(sprintf('%sRF.mat',RFModelSavePath),'nLeaf','nTree',...
'RandomNumber','RFModel','RFPredictConfidenceInterval','RFPredictYield','RFr','RFRMSE',...
'TestVARI','TestYield','TrainVARI','TrainYield');
%精度评定
R2=1-sum((RFPredictYield-TestYield).^2)/sum((output-mean(output)).^2);5.3 SVR向量回归算法
import scipy.io as scio
import numpy as np
from sklearn import metrics
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
matdata=scio.loadmat("data.mat")
AGB=matdata["AGB"].flatten()
ARVI=matdata["ARVI"].flatten()
NDVI=matdata["NDVI"].flatten()
OSAVI=matdata["ARVI"].flatten()
SR=matdata["ARVI"].flatten()
VIGreen=matdata["ARVI"].flatten()
data=matdata["data1"]
from sklearn.svm import SVR
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
C = 6.0 # 惩罚项参数
epsilon = 0.001 # ε-tube宽度
model = SVR(C=C, epsilon=epsilon)
# 拟合模型
X_train, X_test, y_train, y_test = train_test_split(data, AGB, test_size=1/3, random_state=42)
print(model.fit(X_train, y_train))
# 预测
y_train_pred = model.predict(X_train)
#预测值
y_test_pred = model.predict(X_test)
#模型评估
train_rmse = mean_squared_error(y_train, y_train_pred, squared=False)
test_rmse = mean_squared_error(y_test, y_test_pred, squared=False)
print("训练集RMSE:",train_rmse)
print("测试集RMSE:",test_rmse)
train_r=metrics.r2_score(y_train, y_train_pred)
test_r=metrics.r2_score(y_test, y_test_pred)
print("训练集R2:",train_r)
print("测试集R2:",test_r)
print("回归分析")
T_y=np.array(y_test_pred).reshape((len(y_test_pred),1))
T_x=np.array(y_test).reshape((len(y_test),1))
slope,intercept=np.polyfit(y_test,y_test_pred,1)
import seaborn as sns
plt.rcParams['font.sans-serif'] = ['SimHei'] # 中文字体设置-黑体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
ax=sns.regplot(x=T_x,y=T_y,marker="+")
plt.title("SVR-支持向量回归拟合结果(R^2=0.404,RMSE=43.925(Mg/ha))")
plt.legend(["原始数据点",'拟合曲线',"置信区间"])
plt.ylabel("AGB预测值(Mg/ha)")
plt.xlabel("AGB实际测量值(Mg/ha)")
plt.savefig("SVR")
plt.show()
六、生物量反演
%使用RF模型进行反演
ARVI_data=readgeoraster("ARVI.tif");
VIGreen_data=readgeoraster("VIGreen.tif");
NDVI_data=readgeoraster("NDVI.tif");
SR_data=readgeoraster("SR.tif");
OSAVI_data=readgeoraster("OSAVI.tif");
AGB_predict=zeros(size(ARVI_data,1),size(ARVI_data,2));
%使用以上五个参数进行反演
for i=1:1:size(ARVI_data,1)
length=size(ARVI_data,2);
ARVI=ARVI_data(i,1:length);
VIGreen=VIGreen_data(i,1:length);
NDVI=NDVI_data(i,1:length);
SR=SR_data(i,1:length);
OSAVI=OSAVI_data(i,1:length);
data=[SR',NDVI',OSAVI',ARVI',VIGreen'];
[predict_result,interval]=predict(RFModel,data);
AGB_predict(i,1:length)=predict_result;
end
%完成训练后输出mat文件
5.导出反演后tif图像(Python)
import scipy.io as scio
import gdal
import numpy as np
matdata=scio.loadmat("AGB_predict.mat")
AGB=matdata['AGB_predict']
driver=gdal.GetDriverByName("GTiff")
dataset=driver.Create(r'AGB_predict.tif',400,266,1,gdal.GDT_Float32)
band=dataset.GetRasterBand(1)
band.WriteArray(AGB)