【DP】背包问题
一.概念
DP(Dynamic Programming)背包问题是一个经典的组合优化问题,通常用于解决如何在有限的背包容量下,选择一组物品装入背包以最大化某种价值(通常是总价值或总利润)的问题。这个问题有多个变种,解决DP背包问题的常见方法是使用动态规划算法,通常包括以下步骤:
-
定义状态:确定问题的状态,通常包括背包的容量和可选的物品。
-
状态转移方程:根据问题的性质,建立状态之间的转移关系,以描述如何根据之前的状态来更新当前状态。这是解决问题的核心部分。
-
初始化:初始化动态规划表格或数组,通常将边界条件设置为0或者负无穷,以确保正确的状态更新。
-
填充表格:按照状态转移方程,填充动态规划表格或数组,计算出每个状态对应的最优值。
-
回溯或提取结果:根据填充好的表格,可以回溯找到最优解,或者直接从表格中提取最优值。
DP背包问题是算法和计算机科学中的经典问题,有许多优化和变种。不同的问题可能需要不同的动态规划方法和技巧来解决。
二.01背包
(1)介绍
01背包问题是背包问题中的一种常见变种。在01背包问题中,有一组物品,每个物品有一个固定的重量和一个对应的价值,而背包有一个固定的容量限制。每个物品要么放入背包一次,要么不放入,即每个物品的放入决策是离散的,要么选中,要么不选中,因此称为"01"背包。
问题的目标是在背包容量限制下,选择物品放入背包,使得背包中物品的总重量不超过背包容量,同时总价值最大化。
解决01背包问题的一种常见方法是使用动态规划。以下是解决01背包问题的一般步骤:
-
定义状态:通常使用一个二维数组或矩阵来表示状态。dp[i][j] 表示前i个物品放入容量为j的背包中所能获得的最大价值。
-
状态转移方程:状态转移方程描述了如何从之前的状态推导出当前状态。对于01背包问题,状态转移方程通常如下:
dp[i][j] = max(dp[i-1][j], dp[i-1][j - weight[i]] + value[i])
其中,dp[i][j]表示考虑前i个物品,在背包容量为j时的最大价值,weight[i]表示第i个物品的重量,value[i]表示第i个物品的价值。这个方程的含义是,在考虑放入第i个物品或不放入的情况下,选择能获得最大价值的方式。
-
初始化:将dp数组的第一行和第一列初始化为0,因为容量为0时无法放入任何物品,价值为0。
-
填充表格:按照状态转移方程,从左上角开始逐步填充dp数组,直到右下角,得到最优解。
-
回溯或提取结果:通过回溯dp数组,可以确定具体哪些物品被放入了背包,以及它们的总价值。
这种动态规划方法可以有效解决01背包问题,但要注意,对于大规模的问题,可能需要优化存储空间或使用其他算法。
(2)例题
P1048 [NOIP2005 普及组] 采药 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
(3)参考代码
?
#include
using namespace std;
int t[105],v[101];
int dp[1005];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>t[i]>>v[i];
}
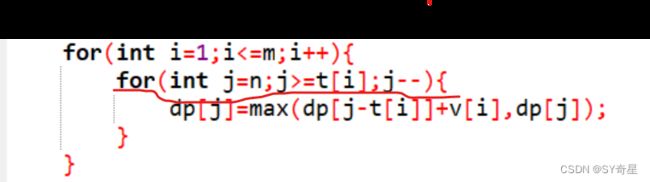
for(int i=1;i<=m;i++){
for(int j=n;j>=t[i];j--){
dp[j]=max(dp[j-t[i]]+v[i],dp[j]);
}
}
cout< 三.完全背包
(1)介绍
完全背包(Unbounded Knapsack)问题是背包问题的一个变种,它与0-1背包问题有些相似,但有一个重要的区别:在完全背包问题中,每种物品可以无限次地选择放入背包中,而不是仅能选择一次或不选。
具体来说,完全背包问题包括以下要素:
-
一组不同种类的物品,每种物品都有一个固定的重量(weight[i])和一个对应的价值(value[i])。
-
一个容量限制的背包,它能够容纳的最大总重量为 W。
问题的目标是选择这些物品,使得它们的总重量不超过背包的容量 W,同时总价值最大化。
解决完全背包问题的方法通常使用动态规划。以下是解决完全背包问题的一般步骤:
-
定义状态:通常使用一个一维或二维数组 dp 来表示状态。dp[i] 表示背包容量为 i 时所能获得的最大价值。
-
状态转移方程:状态转移方程描述了如何从之前的状态推导出当前状态。对于完全背包问题,状态转移方程通常如下:
dp[i] = max(dp[i], dp[i - weight[j]] + value[j])
其中,i 表示当前背包的容量,weight[j] 表示第 j 种物品的重量,value[j] 表示第 j 种物品的价值。这个方程的含义是,在考虑放入第 j 种物品多次或不放入的情况下,选择能获得最大价值的方式。
-
初始化:将 dp 数组初始化为0,因为容量为0时价值总是0。
-
填充表格:按照状态转移方程,从背包容量小到大逐步填充 dp 数组,直到容量为 W,得到最优解。
-
提取结果:dp[W] 就是问题的最优解,它表示容量为 W 时所能获得的最大价值。
通过这个动态规划方法,你可以解决完全背包问题,找到放入背包的最佳物品组合,以最大化总价值。完全背包问题在实际中有许多应用,如资源分配、货物装载等。
(3)不同点:
只需要将
改成for(int j=t[i];j<=n;j++) 即可
四.多重背包
(1)介绍
多重背包(Multiple Knapsack)问题是背包问题的另一种变种,它与0-1背包问题和完全背包问题都有所不同。在多重背包问题中,每种物品有一个固定的重量、一个对应的价值,但是每种物品有限制的数量可供选择放入背包中。这个问题可以描述为:有一组不同种类的物品,每种物品都有一个重量(weight[i])、一个价值(value[i])以及一个数量限制(quantity[i]),还有一个背包的容量限制(W)。问题的目标是选择这些物品,使得它们的总重量不超过背包的容量 W,同时总价值最大化,但不能超过每种物品的数量限制。
解决多重背包问题的方法通常也使用动态规划,但相对于完全背包问题,需要在状态转移方程中考虑每种物品的数量限制
(2)办法
使用二进制思想,如a物品v=3,c=6,有8个,则把1个物品合为a1,v=3,c=6;第二个物品合成2个:a2,v=6,c=12;第三个物品合成4个,a3,v=12,c=24;然后二进制不够分了,就把剩余的分为一组,a4,v=3,c=6;
分完后再01背包即可
五.分组背包
(1)介绍
分组背包(Group Knapsack)问题是背包问题的另一种变体,它与传统的0-1背包问题、完全背包问题以及多重背包问题都有一些不同。在分组背包问题中,物品被分成多个组(或者称为类别),每个组内包含若干物品,每个物品都有自己的重量和价值。问题的目标是选择一个或多个组,以及每个选中的组中的一个或多个物品,使得选中的物品总重量不超过背包的容量限制,同时总价值最大化。
(2)解决方案
三重循环即可,同01背包