导读Emergence of Polarization in Coevolving Networks
The emergence of polarization in coevolving networks

正文
社交媒体中的意见分化现象很普遍,而现有的网络建模工作已经发现极化现象。但是,如何控制极化的定量方法和理论框架尚未建立。最新研究发现了观点分布的统一标度定律,并提出了一个共演化理论框架,可以将观点动力学和网络演化统一起来。该理论已在Facebook和博客社区的经验数据中得到验证,不仅解释了社交网络标度律,还能够定量预测标度系数。
意见极化是指意见的对立随时间推移而增加的过程,常见于政治领域和社交媒体。实证研究发现存在双极化模式,即个体被划分为两组,意见完全相反。但对于某些系统而言,存在一种去极化阶段,其中意见分布在一个中性状态周围峰值,并且在非政治领域存在显著的方差。
社交网络中的回声室效应是意见极化的基础,意见极化和网络结构的共存意味着意见和网络动态之间的相互作用在极化中发挥了关键作用。尽管已经提出了生长的共同演化模型来理解意见和网络结构之间的相互作用,但这些研究并没有专门关注意见极化。
最近提出了一个加强的共同演化模型,解释了网络极化现象。该模型有稳定的单极化阶段和全局共识阶段,但只有暂时的双极化阶段。现有极化模型框架是同步模型的变化,而双极化需要不同的框架。共同演化网络模型因意见和网络结构之间的复杂相互作用而难以解决。因此,现有模型依赖于数值模拟和定性近似,缺少一个量化模型。
极化动力学有两种普遍机制:首先是意见同化,即个人观点在社交网络中受到邻居的影响,并且倾向与同类观点融合;其次是同质性聚集,即社会联系随着时间而发展,个人倾向于与具有相似观念的人建立联系。这两种机制导致了网络演化和观点动力学纠缠于真实的社会网络中。
基于此背景,研究者提出了共演化网络框架,捕捉观点动力学和网络演化之间的相互作用。该框架可以预测到网络演化的三个阶段:①极化,②部分极化,③去极化。
研究者使用两个数据集。一个是Facebook上最多的500个领域数据,这些领域被分为硬内容(FB-HC,如国家新闻、政治或国际事务)和软内容(FB-SC,体育、娱乐或旅行),对于每个领域,测量不同政治观点的比例,从而计算每种政治倾向的平均得分。另一个数据集Blogosphere收集了1490个博客,博客之间相互引用了上万次,从而可以构建其社交网络,并且由-1(自由)到1(保守)为其观点分类。
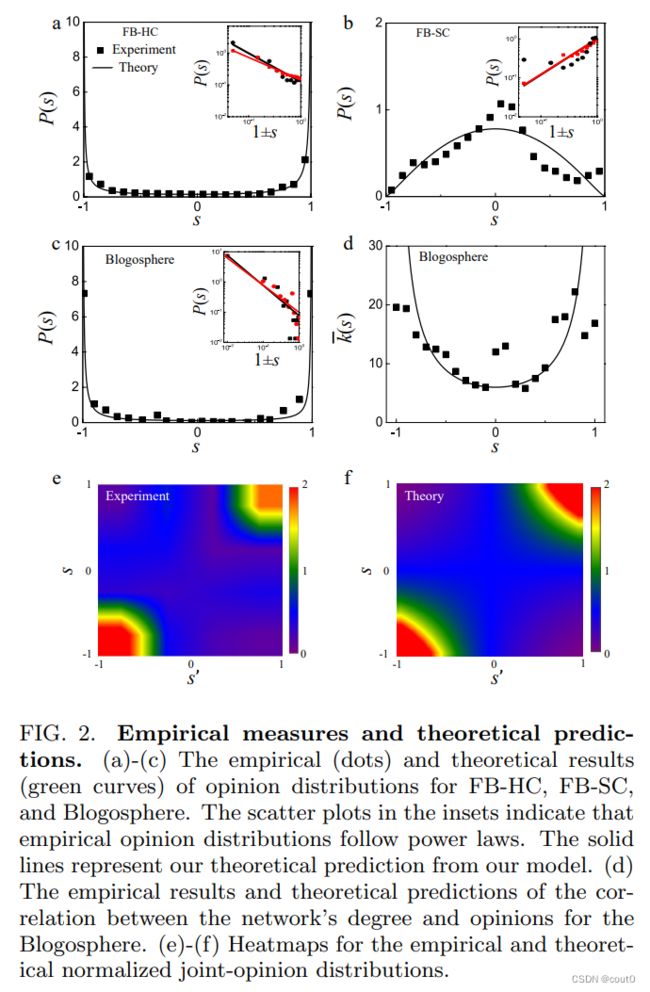
为了量化观察到的极化现象,图2a-c中的散点图描述了所有三个实证数据集的观点分布P(s)。研究者发现两个政治相关的数据集(FB-HC和Blogosphere)的观点分布是U型的,表明存在极化阶段。相比之下,FB-SC数据集中的观点分布是反U型分布的,表明存在去极化阶段。
为了研究人口规模和观点极端程度之间的缩放关系,研究者在图2a-c的插图中将P(s)作为1±s的函数绘制,其中1±s测量观点偏离最极端±1的程度。研究者发现P(s)满足幂律函数,即
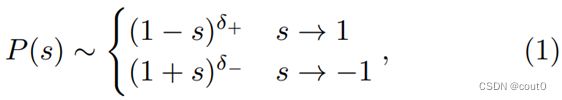
其中 δ ± δ_± δ±表示当观点 s s s接近 ± 1 ±1 ±1时的幂律指数。 δ ± δ± δ±为负时表示人口随着他们的观点极端化而增加,并且当观点得分 s s s达到极限情况 ± 1 ±1 ±1时趋于发散。相反, δ ± δ_± δ±为正时表示 P ( s ) P(s) P(s)在 0 0 0附近取得峰值。因此,指数 δ ± δ_± δ±表征极化,即极化系统的 δ ± < 0 δ_±<0 δ±<0且去极化系统的 δ ± > 0 δ_±>0 δ±>0。
为了探索观点极化对网络结构的影响,研究者测量了Blogosphere数据集中平均度数 k ˉ \bar{k} kˉ作为观点 s s s的函数。图2d中的散点图显示 k ˉ \bar{k} kˉ随着观点得分s的极端化而增加,表明持有极端政治观点的用户更有可能成为网络的中心。研究者还在Blogosphere网络的每条边上测量了联合观点分布 Q ( s , s ′ ) Q(s,s') Q(s,s′),该分布计算了具有观点的个体连接到具有观点 s ′ s' s′的另一个个体的边的数量。图2e绘制了归一化的联合观点分布 R ( s , s ′ ) = Q ( s , s ′ ) ( P ( s ) P ( s ′ ) ) R(s,s')=\frac{Q(s,s')}{(P(s)P(s'))} R(s,s′)=(P(s)P(s′))Q(s,s′),测量与不相关分布的偏差。研究者发现,具有相似观点的两个连接代理的数量显著增加,而具有不同观点的两个连接代理的数量受到抑制,表明现实世界社交网络中存在同质性聚类(图1a)。
为了解释经验观察结果,研究者考虑一个共同演化网络,由 N N N个交互代理组成,每个代理人都有一个意见 s s s,在 − 1 −1 −1到 1 1 1之间连续变化。代理人之间的连接由邻接矩阵 A A A描述,其中矩阵元素 A i j = 1 A_ij=1 Aij=1或 0 0 0表示代理人 i i i与 j j j连接或断开。代理人的意见和他们之间的连接在连续时间 t t t内同时演化。此外,研究者要求意见动态和网络演化相互耦合,满足两个内在机制:①意见同化,即代理人的意见变化受其邻居的意见影响,并倾向于变成类似的观点。②同质性聚类,描述社交连接更有可能在代理人持有相似观点的情况下建立。这两种机制与意见和社交联系的共同演化动态相互耦合。下面详细讨论研究者所提出的共同演化动力学。
为了模拟意见同化,研究者假设意见动态遵循公式
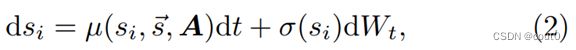
其中 s ⃗ = ( s 1 , s 2 , … , s N ) \vec{s}=(s_1,s_2,\dots,s_N) s=(s1,s2,…,sN)表示所有代理的意见集, s i s_i si是代理 i i i的意见。 A A A是代理的邻接矩阵, W t W_t Wt是标准维纳过程。 μ \mu μ是控制意见变化的漂移项, σ \sigma σ是控制意见动态方差的扩散项。此外,研究者假设意见漂移 μ \mu μ取决于代理 i i i和其邻居的意见,满足公式
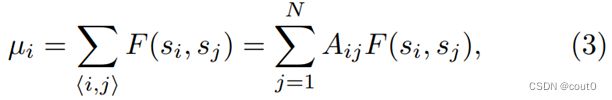
其中 < i , j >
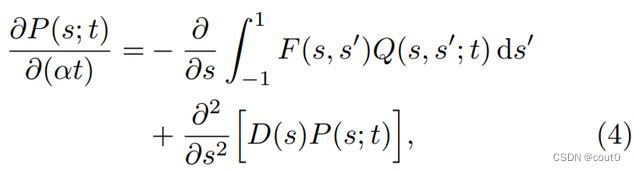
捕获了邻居间的相互作用,因为 Q ( s , s ′ ; t ) Q(s,s';t) Q(s,s′;t)隐含地依赖于底层网络 A A A。
为了建立同质性聚类模型,研究者假设持有相似意见的代理更可能相互连接。具体来说,代理 i i i会以概率 γ + ( s i , s j ) N \frac{\gamma_+(s_i,s_j)}{N} Nγ+(si,sj)连接到未连接的代理 j j j以构建一个新边,其中 s i s_i si和 s j s_j sj分别是代理 i i i和 j j j的意见。因子 1 N \frac{1}{N} N1保证网络的稀疏性。同时,代理 i i i会以概率 γ − ( s i , s j ) \gamma_-(s_i,s_j) γ−(si,sj)与已连接的代理断开连接,导致现有边消失。也就是说:
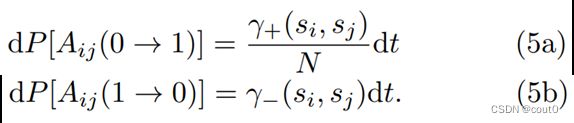
为了捕捉同质聚类,研究者假设 γ ± \gamma_± γ±取决于代理 i i i及其邻居 j j j的观点,这种依赖性导致了网络演化与意见动态的耦合。
然而,研究者注意到在大多数社交媒体中,意见改变的速度远远慢于网络演化。为了量化它们之间的相对时间尺度,研究者通过一个因子 α \alpha α对意见漂移 F F F和扩散 D D D进行了重新缩放,表示它们与网络演化之间的更新率之间的关系。在 α \alpha α的幂级数展开方面,研究者发现联合意见分布(, ^′;)的时间演化满足:
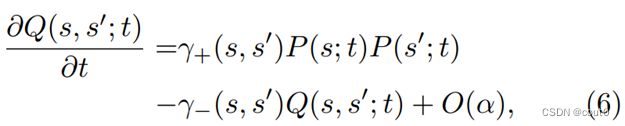
其中 ο ( α ) \omicron(\alpha) ο(α)项捕获更高阶的修正。在以下讨论中,研究者将保持 α → 0 \alpha\to0 α→0的极限状态,即网络演化在绝热近似下进行,而在该绝热近似下, ο ( α ) \omicron(\alpha) ο(α)将被省略。
研究者给出了所提出框架的稳态解。方程(6)导致稳态联合意见分布 Q s t ( s , s ′ ) = γ + ( s , s ′ ) γ − ( s , s ′ ) ) P s t ( s ) P s t ( s ′ ) Q_st(s,s')=\frac{\gamma_+(s,s')}{\gamma_-(s,s'))}P_s{t}(s)P_{st}(s') Qst(s,s′)=γ−(s,s′))γ+(s,s′)Pst(s)Pst(s′),其中 P s t ( s ) P_{st}(s) Pst(s)是稳态意见分布。代入方程(4)得到 ∫ − 1 1 K ( s , s ′ ) P s t ( s ′ ) d s ′ = l n ( D ( s ) P s t ( s ) ) \int_{-1}^1K(s,s')P_{st}(s')ds'=ln(D(s)P_{st}(s)) ∫−11K(s,s′)Pst(s′)ds′=ln(D(s)Pst(s)),其中核 K ( s , s ′ ) ≡ γ + ( ± 1 , s ′ ) F ( s , s ′ ) γ − ( ± 1 , s ′ ) D ( s ) d s K(s,s')\equiv\frac{\gamma_+(\pm1,s')F(s,s')}{\gamma_-(\pm1,s')D(s)}ds K(s,s′)≡γ−(±1,s′)D(s)γ+(±1,s′)F(s,s′)ds。当 s → ± 1 s\to\pm1 s→±1时,研究者发现 ( ∫ − 1 1 K ± ( s ′ ) P s t ( s ′ ) d s ′ ) l n ( 1 ∓ s ) ∼ l n [ ( 1 ∓ s ) P s t ( s ) ] (\int_{-1}^1K_\pm(s')P_{st}(s')ds')ln(1\mp s)\sim ln[(1\mp s)P_st(s)] (∫−11K±(s′)Pst(s′)ds′)ln(1∓s)∼ln[(1∓s)Pst(s)],其中 K ∓ ( s ′ ) ≡ γ + ( ± 1 , s ′ ) F ( ± 1 , s ′ ) γ − ( ± 1 , s ′ ) σ 2 K_\mp(s')\equiv \frac{\gamma_+(\pm1,s')F(\pm1,s')}{\gamma_-(\pm1,s')\sigma^2} K∓(s′)≡γ−(±1,s′)σ2γ+(±1,s′)F(±1,s′)。
因此,研究者的理论预测通用的比例定律 P s t ( s ) ∼ ( 1 ∓ s ) δ ± P_{st}(s)\sim(1\mp s)^{\delta\pm} Pst(s)∼(1∓s)δ±,其中指数 δ ± = ∫ − 1 1 K ± ( s ′ ) P s t ( s ′ ) d s ′ − 1 \delta_\pm=\int_{-1}^1K_\pm(s')P_{st}(s')ds'-1 δ±=∫−11K±(s′)Pst(s′)ds′−1,与在真实世界网络中发现的比例定律相吻合。这一发现表明,通用比例定律对于共同进化的网络而言是相当普遍的,并且在微观细节上基本独立。
方程6表明网络结构和观点之间的潜在相关性。将方程4-5与方程6结合起来得到规范化的联合意见分布 R ( s , s ′ ) = Q ( s , s ′ ) P ( s ) P ( s ′ ) = γ + ( s , s ′ ) γ − ( s , s ′ ) R(s,s')=\frac{Q(s,s')}{P(s)P(s')}=\frac{\gamma_+(s,s')}{\gamma_-(s,s')} R(s,s′)=P(s)P(s′)Q(s,s′)=γ−(s,s′)γ+(s,s′)。
由于联合意见分布 Q ( s , s ′ ) Q(s,s') Q(s,s′)统计了具有意见 s s s和 s ′ s' s′的两个代理之间连接的数量。因此,具有意见 s s s的代理的预期度数可以表示为: k ˉ = ∫ − 1 1 Q ( s ′ ) s ′ d s ′ = ∫ − 1 1 Q ( s , s ′ ) P ( s ) d s ′ = ∫ − 1 1 s ′ P s t ( s ′ ) γ + ( s ′ , s ) γ − ( s ′ , s ) \bar{k}=\int_{-1}^1Q(s')s'ds'=\int_{-1}^1\frac{Q(s,s')}{P(s)}ds'=\int_{-1}^1s'P_{st}(s')\frac{\gamma_+(s',s)}{\gamma_-(s',s)} kˉ=∫−11Q(s′)s′ds′=∫−11P(s)Q(s,s′)ds′=∫−11s′Pst(s′)γ−(s′,s)γ+(s′,s)从而使研究者能够预测网络度量 k ˉ \bar{k} kˉ与意见 s s s之间的相关性。
为了将研究者的理论与实验数据进行比较,下面研究者将专注于提出的框架的最小实现。具体来说,研究者使用线性意见动力学模型, F ( s , s ′ ) = λ ( s ′ − s ) F(s,s')=\lambda(s'-s) F(s,s′)=λ(s′−s),其中 λ \lambda λ是控制意见变化速率的常数。研究者还假设边缘出生和死亡速率满足 γ ± ( s , s ′ ) = ρ ± ( 1 + J ± s s ′ ) \gamma_\pm(s,s')=\rho_\pm(1+J_\pm ss') γ±(s,s′)=ρ±(1+J±ss′),其中 J ± ≤ 1 J_\pm\le1 J±≤1量化同质性聚类的强度,即类似的个体建立关系的能力。研究者发现了最小模型的核函数 K ( s , s ′ ) = g ∫ 1 + J + s s ′ 1 + J − s s ′ 2 ( s ′ − s ) 1 − s 2 K(s,s')=g\int\frac{1+J_+ss'}{1+J-_ss'}\frac{2(s'-s)}{1-s^2} K(s,s′)=g∫1+J−ss′1+J+ss′1−s22(s′−s)的显式形式,其中参数 g ≡ λ σ 0 2 ρ + ρ − g\equiv\frac{\lambda}{\sigma_0^2}\frac{\rho+}{\rho-} g≡σ02λρ−ρ+。这里 λ σ 0 2 \frac{\lambda}{\sigma_0^2} σ02λ表示意见同化速率, ρ + ρ − \frac{\rho+}{\rho-} ρ−ρ+是网络连接的出生-死亡比率。参数 g g g集成了意见和网络动态的相互作用强度。结合公式(4和6),研究者针对最小模型( < s > ≠ 0 \ne0 <s>=0)求解 P ( s ) P(s) P(s),发现研究者的预测与实验数据一致(图2a-c)。最小模型也可以生成不对称的 P ( s ) P(s) P(s)分布,如图2a-c所示。但是,实验数据测得的平均意见 < s > <s>很接近于零,这意味着相应的 P ( s ) P(s) P(s)可以很好地近似为对称分布。为简单起见,以下讨论将仅关注对称情况( < s > ≠ 0 \ne0 <s>=0) 。
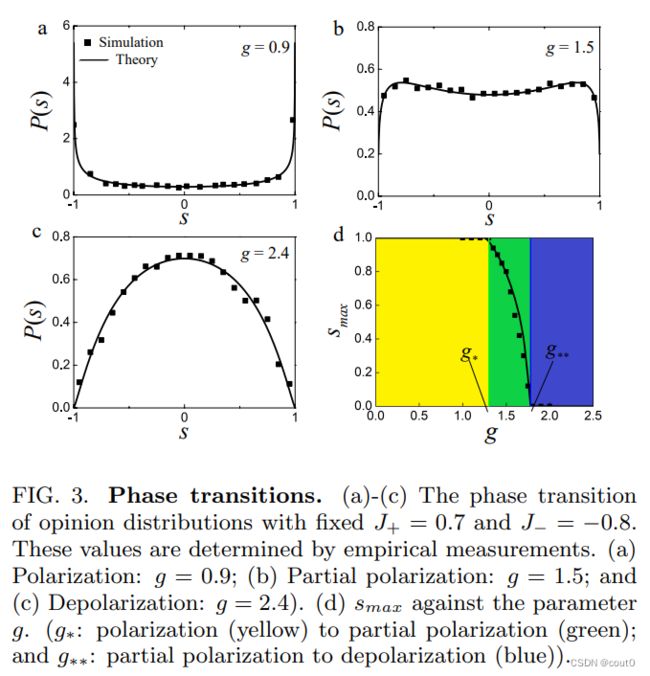
为了探索不同的相位,研究者对固定 J + J_+ J+和 J − J_- J−的各种 g g g进行数值模拟。图1b展示了一个 2000 2000 2000个节点的模拟最小模型,与图1a中的实验网络呈现出定性相似性。图3a展示了当 g g g较小时( g ≈ 0.9 g\approx0.9 g≈0.9)出现一个双极化的U形态观点分布 P ( s ) P(s) P(s)。逐渐增加观点变化率,研究者发现 P ( s ) P(s) P(s)从形态向形态过渡,表明了部分极化。当 g g g值足够大时( g ≈ 2.4 g\approx2.4 g≈2.4), P ( s ) P(s) P(s)变为去极化的反形态分布。为了量化不同的相位,研究者定义一个序参量 s m a x = ∣ ( a r g m a x s P ( s ) ) ∣ s_{max}=|(argmax_sP(s))| smax=∣(argmaxsP(s))∣,表示最可能的观点。研究者发现,去极化相位(图3c)时 s m a x = 0 s_{max}=0 smax=0,极化相位(图3a)时 s m a x = 1 s_{max}=1 smax=1。对于部分极化相位, s m a x s_{max} smax在 0 0 0和 1 1 1之间变化(图3b)。图3d以 g g g为函数绘制 s m a x s_{max} smax ,表明存在两个相位转变。第一个相位转变发生在 s ∗ ≈ 1.3 s_*\approx1.3 s∗≈1.3时, s m a x s_{max} smax偏离 1 1 1,表明系统从极化向部分极化转变。第二个相位转变发生在 s ∗ ≈ 1.78 s_*\approx1.78 s∗≈1.78时, s m a x s_{max} smax消失,表明部分极化向去极化转变。总的来说,减小 g g g会使系统向极化方向移动。事实上,较小的观点同化率使观点远离同化,向极化方向发展。另一方面,较大的出生-死亡比率会降低不同的代理连接的机会,因此,类似的代理倾向于与其观点同化的代理聚集在一起,导致极化。
为了探究观点拓扑结构的相关性,研究者在图2f中绘制了预测的归一化联合观点分布 R ( s , s ′ ) = γ + ( s , s ′ ) γ − ( s , s ′ ) = ρ + ( 1 + J + s s ′ ) ρ − ( 1 + J − s s ′ ) R(s,s')=\frac{\gamma_+(s,s')}{\gamma_-(s,s')}=\frac{\rho_+(1+J_+ss')}{\rho_-(1+J_-ss')} R(s,s′)=γ−(s,s′)γ+(s,s′)=ρ−(1+J−ss′)ρ+(1+J+ss′),显示出两个相反的聚集域,分别在左下和右上角,与实证观察结果(图2e)一致。图2d描述了对 k ˉ ( s ) \bar{k}(s) kˉ(s)的分析预测,与实证测量结果一致。实证数据显示中立个体存在一个小峰值,这意味着相对于研究者的理论,这些用户预计具有较大的度数。这种差异可能是由于一小群政治中立的独立媒体吸引了两个阵营的大量连通性。研究者将把这种现象留待未来研究。这个预测表明,研究者的模型生成了两个高度极化的集群(图1b),其中心节点表现出明显的极端性,与现实世界的极化网络(图1a)一致。
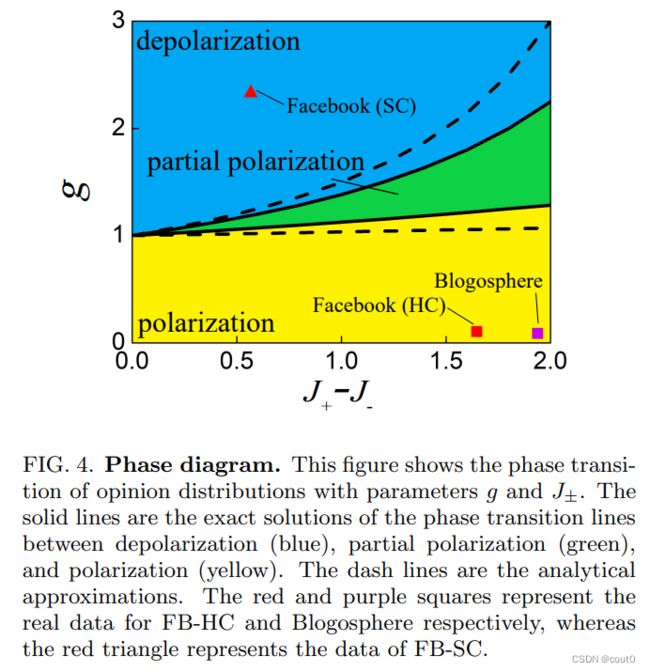
由于研究者的理论成功地捕捉了极化和去极化阶段,因此人们可能会想知道建模参数如何控制不同阶段。为了简化起见,研究者仅关注对称情况,即 < s > = 0 =0 <s>=0。如上所述,指数 δ < 0 \delta<0 δ<0用于极化阶段,而指数 δ > 0 \delta>0 δ>0用于部分极化和去极化阶段。因此,当指数 δ = 0 \delta=0 δ=0时,极化和部分极化之间的转变出现,导致 g ∗ − 1 + ( J + − J − ) f ( J − ) = 1 g_*^{-1}+(J_+-J_-)f(J_-)=1 g∗−1+(J+−J−)f(J−)=1,其中 f ( J − ) = ( 1 + J − ) ∫ − 1 1 d s ′ s ′ 2 1 − J s ′ 2 2 P s t ( s ′ ) f(J_-)=(1+J_-)\int_{-1}^1ds'\frac{s'^2}{1-J_{s'^2}^2}P_{st}(s') f(J−)=(1+J−)∫−11ds′1−Js′22s′2Pst(s′)。
对于部分极化和去极化相之间的转变,当 s = 0 s=0 s=0时,一阶导数为零,即 P ′ ( 0 ) = 0 P'(0)=0 P′(0)=0,因为存在对称性。然而,对于呈形的 P ( s ) P(s) P(s),其二阶导数 P s t ′ ′ ( 0 ) > 0 P_{st}''(0)>0 Pst′′(0)>0,而对于呈反向形的 P ( s ) P(s) P(s),其二阶导数 P s t ′ ′ ( 0 ) < 0 P_{st}''(0)<0 Pst′′(0)<0。因此,当二阶导数为零时,即 P s t ′ ′ ( 0 ) = 0 P_{st}''(0)=0 Pst′′(0)=0时,转变发生。将 P s t ′ ( 0 ) = 0 P_{st}'(0)=0 Pst′(0)=0和 P s t ′ ′ ( 0 ) = 0 P_{st}''(0)=0 Pst′′(0)=0代入方程(4),研究者得到 g ∗ ∗ − 1 + ( + − J − ) < s 2 > = 1 g_{**}^{-1}+(_+-J_-)
研究者通过实证研究发现了一种观点分布的普适尺度定律,它由一组尺度指数来描述,使研究者能够量化真实社会系统中的不同极化相。研究者提出了一种共同进化网络的极化动力学通用框架,其中基于两个因素耦合了观点动力学和网络演化。与现有的RM模型相比,研究者的模型预测了稳定的双极化相和去极化相。特别地,研究者的理论在分析上与实证观察一致地找到了双极化的观点分布和网络结构。此外,研究者的框架提供了共同进化网络动力学的确切解决方案,它不仅考虑到观察到的尺度定律,还预测了相应的三个不同相的相图。另一方面,研究者的解析解是在绝热近似下发现的。研究者将把寻找普遍解的任务留给未来的研究。研究者的理论提供了一个通用框架,可以应用于其他领域。例如,通过引入 s i = c o s ( θ i ) s_i=cos(\theta_i) si=cos(θi),该框架能够模拟涉及背景变化的非线性耦合振荡器。最重要的是,研究者的结果可能影响跨学科理解社会科学和政治科学中的人类社会。