机器学习笔试面试题——day4
选择题
2、我们想在大数据集上训练决策树, 为了使用较少时间, 我们可以
A 增加树的深度
B 增加学习率 (learning rate)
C 减少树的深度
D 减少树的数量
增加树的深度, 会导致所有节点不断分裂, 直到叶子节点是纯的为止. 所以, 增加深度, 会延长训练时间.
决策树没有学习率参数可以调. (不像集成学习和其它有步长的学习方法)
决策树只有一棵树, 不是随机森林。
3、假如我们使用非线性可分的SVM目标函数作为最优化对象, 我们怎么保证模型线性可分?
A 设C=1
B 设C=0
C 设C=无穷大
D 以上都不对
C无穷大保证了所有的线性不可分都是可以忍受的.
4、以下哪些算法, 可以用神经网络去构造:
KNN
线性回归
对数几率回归
A 1和 2
B 2 和 3
C 1, 2 和 3
D 以上都不是
KNN算法不需要训练参数, 而所有神经网络都需要训练参数, 因此神经网络帮不上忙
最简单的神经网络, 感知器, 其实就是线性回归的训练
我们可以用一层的神经网络构造对数几率回归
5、请选择下面可以应用隐马尔科夫(HMM)模型的选项
A 基因序列数据集
B 电影浏览数据集
C 股票市场数据集
D 所有以上
6、我们建立一个5000个特征, 100万数据的机器学习模型. 我们怎么有效地应对这样的大数据训练 :
A 我们随机抽取一些样本, 在这些少量样本之上训练
B 我们可以试用在线机器学习算法
C 我们应用PCA算法降维, 减少特征数
D B 和 C
E A 和 B
F 以上所有
7、我们想要减少数据集中的特征数, 即降维. 选择以下适合的方案 :
使用前向特征选择方法
使用后向特征排除方法
我们先把所有特征都使用, 去训练一个模型, 得到测试集上的表现. 然后我们去掉一个特征, 再去训练, 用交叉验证看看测试集上的表现. 如果表现比原来还要好, 我们可以去除这个特征.
查看相关性表, 去除相关性最高的一些特征
A 1 和 2
B 2, 3和4
C 1, 2和4
D All
8、对于随机森林和GradientBoosting Trees, 下面说法正确的是:
1 在随机森林的单个树中, 树和树之间是有依赖的, 而GradientBoosting Trees中的单个树之间是没有依赖的
2 这两个模型都使用随机特征子集, 来生成许多单个的树
3 我们可以并行地生成GradientBoosting Trees单个树, 因为它们之间是没有依赖的
4 GradientBoosting Trees训练模型的表现总是比随机森林好
A2
B1 and 2
C1, 3 and 4
D2 and 4
1 随机森林是基于bagging的, 在随机森林的单个树中, 树和树之间是没有依赖的。
2 Gradient Boosting trees是基于boosting的,且GradientBoosting Trees中的单个树之间是有依赖关系。
3 这两个模型都使用随机特征子集, 来生成许多单个的树。
9、对于PCA(主成分分析)转化过的特征 , 朴素贝叶斯的”不依赖假设”总是成立, 因为所有主要成分是正交的, 这个说法是 :
A正确的
B错误的
10、对于PCA说法正确的是 :
我们必须在使用PCA前规范化数据
我们应该选择使得模型有最大variance的主成分
我们应该选择使得模型有最小variance的主成分
我们可以使用PCA在低维度上做数据可视化
A1, 2 and 4
B2 and 4
C3 and 4
D1 and 3
E1, 3 and 4
14、对应GradientBoosting tree(GBDT)算法, 以下说法正确的是:
当增加最小样本分裂个数,我们可以抵制过拟合
当增加最小样本分裂个数,会导致过拟合
当我们减少训练单个学习器的样本个数,我们可以降低variance
当我们减少训练单个学习器的样本个数,我们可以降低bias
A2 和 4
B2 和 3
C1 和 3
D1 和 4
最小样本分裂个数是用来控制“过拟合”参数。太高的值会导致“欠拟合”,这个参数应该用交叉验证来调节。
bias过高表示样本实际输出与真实值差距过大
variance过高表示模型不稳定手撕代码
1 合并无序链表为有序
//先单链表各自排序,用选择排序,然后再合并,合并的时候pa,pb,哪个指针的数值小,指针+1
//先各自排序,选择排序
public class sort(ListNode pHead){
int temp;
ListNode cur = pHead;
while(cur!=null){
ListNode pNext = cur.next;
while(pNext!=null){
if(pNext.data2 两个队列实现一个栈
/*
栈先进后出,队列先进先出
1 在push的时候,把元素向非空的队列添加
2 在pop的时候,把不为空的队列中的size()-1的元素poll出来,添加到另一个为空的队列中,再把队列中最后的元素poll出来
即始终有一个为空,另一个非空,push到非空,pop把非空转移到空,把最后一个元素出队列
*/
private static Queue3 一个有序数组,找出两个值加起来等于key
//一个有序数组,找出两个值加起来等于key,遍历,找key-arr[i]的值
public int findKey(int[] arr,int key){
Map map = new HashMap<>():
for(int i =0;i 4 桶排序,对于浮点数的排序很有用O(n)
public static void bucketSort(float[] arr) {
// 新建一个桶的集合
ArrayList> buckets = new ArrayList>();
for (int i = 0; i < 10; i++) {
// 新建一个桶,并将其添加到桶的集合中去。
// 由于桶内元素会频繁的插入,所以选择 LinkedList 作为桶的数据结构
buckets.add(new LinkedList());
}
// 将输入数据全部放入桶中并完成排序
for (float data : arr) {
int index = getBucketIndex(data);
insertSort(buckets.get(index), data);
}
// 将桶中元素全部取出来并放入 arr 中输出
int index = 0;
for (LinkedList bucket : buckets) {
for (Float data : bucket) {
arr[index++] = data;
}
}
}
/**
* 计算得到输入元素应该放到哪个桶内
*/
public static int getBucketIndex(float data) {
// 这里例子写的比较简单,仅使用浮点数的整数部分作为其桶的索引值
// 实际开发中需要根据场景具体设计
return (int) data;
}
/**
* 我们选择插入排序作为桶内元素排序的方法 每当有一个新元素到来时,我们都调用该方法将其插入到恰当的位置
*/
public static void insertSort(List bucket, float data) {
ListIterator it = bucket.listIterator();
boolean insertFlag = true;
while (it.hasNext()) {
if (data <= it.next()) {
it.previous(); // 把迭代器的位置偏移回上一个位置
it.add(data); // 把数据插入到迭代器的当前位置
insertFlag = false;
break;
}
}
if (insertFlag) {
bucket.add(data); // 否则把数据插入到链表末端
}
}
}
5 判断a+b>c?要考虑溢出
// 判断a+b>c?要考虑溢出
/*
如果ab同号,那么可能会产生溢出
如果ac同号,那么换成a>c-b判断
如果ac异号,如果a>0那么一定true;如果a<0,那么为false
如果ab异号,直接判断就好
*/
public static boolean compare(int a,int b,int c){
if((a>0&&b>0)||(a<0&&b<0)){
if((a>0&&c>0)||(a<0&&c<0)){
if(a>c-b)
return true;
else
return false;
}else{
if(a>0)
return true;
else
return false;
}
}else{
if(a+b>c)
return true;
else
return false;
}
}机器学习算法
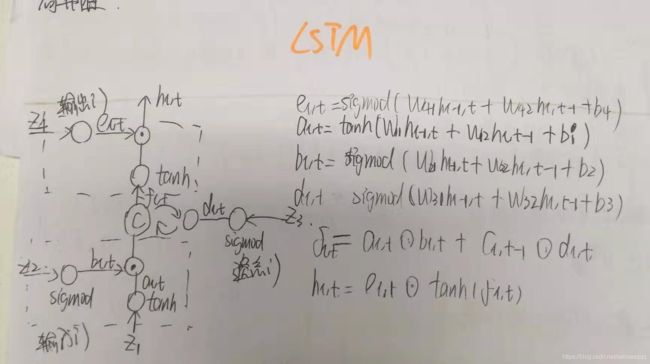
1 LSTM结构图和公式
2 常用的机器学习比如SVM,PCA,iForest有哪些参数
| 常用机器学习算法 | 参数 | 常用机器学习算法 | 参数 |
| SVM | 核函数(线性核、ploy、rbf、sigmod)、损失函数、惩罚系数(C)、多分类策略 | 线性回归 | 截距(b值) |
| PCA | 主成分k | Lasso回归 | b值,正则化系数,迭代次数 |
| iForest | n_ estimators:基学习器的个数(这里是树的颗数),是否用采样法(bootstrap ) | KNN | k值、距离计算方法 |
| GBDT | 学习率,损失函数,n_ estimators, |
3 深度学习调参一般有哪些参数
| 学习率:常用策略1)学习率衰减2)用自使用学习率作为优化器,如Adam和Adagrad |
| mini batch:小的mini batch size可能因为收敛的抖动比较厉害反而不容易卡在局部最低点,但是mini batch也不能太大,反而准确率下降。 |
| epoch:用早停法选择合适核Epoch,观察validation error上升时就early stop,但是别一看到上升就停,再观察一下,因为有可能只是暂时的现象,这时候停止反而训练会不充分 |
| 损失函数:一般来分类是softmax,回归是L2的loss |
| 激活函数:对于梯度消失现象 Sigmoid会发生梯度消失的情况,所以激活函数一般不用,收敛不了了。Tanh(x),没解决梯度消失的问题。 梯度消失的情况,就是当数值接近于正向∞,求导之后就更小的,约等于0,偏导为0 |
| 层数:层数越多越灵敏收敛越好,但是容易过拟合。可以用Drop-out 删除一些无效的节点。 |
| 过拟合:drop-out,BN,batch normalization(归一化) |
| 一些模型类的参数:隐藏层单元数(units)\时间序列模型的步长\RNN的CELL类型(LSTM\GRU) |