【算法导论】分治策略求最大子数组问题分析、伪代码及C代码实现

最大子数组问题

        寻找A的和最大的非空连续子数组，我们称这样的连续子数组为最大子数组。如下所示，A[1..16]的最大子数组为A[8..11]，其和为43，是A的所有子数组中和最大的。

注意： 只有当数组中包含负数时，最大子数组问题才有意义。如果所有数组元素都是非负数，子数组问题没有任何难度，因为整个数组的和肯定最大。

使用分治策略的求解方法

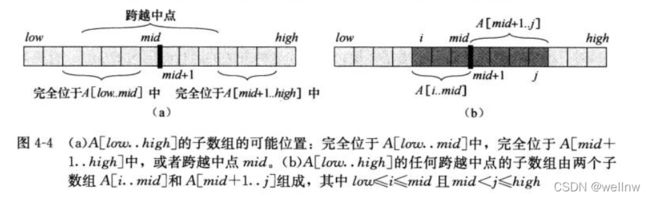
        我们要寻找子数组A[low..high]的最大子数组。使用分治技术意味着我们要将子数组划分为两个规模尽量相等的子数组。也就是说，找到子数组的中央位置，比如mid，然后考虑求解两个子数组A[low..mid]和A[mid+1..high]。如下所示A[low..high]的任何连续子数组A[i..j]所处的位置必然是以下三种情况之一：

        1.完全位于子数组A[low..mid]中，因此low≤i≤j≤mid 

        2.完全位于子数组A[mid+1..high]中，因此mid

        3.跨越了中点，因此low≤i≤mid

        因此，A[low..high]的一个最大子数组所处的位置必然是这三种情况之一。实际A[low..high]的一个最大子数组必然是完全位于A[low..mid]中、完全位于A[mid+1..high]中或者跨越中点的所有子数组中和最大者。我们可以递归地求解A[low..mid]和A[mid+1..high]的最大子数组，因为这两个子问题仍是最大子数组问题，只是规模更小。因此，剩下的全部工作就是寻找跨越中点的最大子数组，然后在三种情况中选取和最大者。

         我们可以很容易地在线性时间（相对于子数组A[low..high]的规模）内求出跨越中点的最大子数组。如上图b所示，任何跨越中点的子数组都是由两个子数组A[i..mid]和A[mid+1..j]组成，其中low≤i≤mid且mid

 FIND-MAX-CORSSING-SUBARRAY伪算法

        FIND-MAX-CORSSING-SUBARRAY接收数组A和下标low、mid和high输入，返回一个下标元组划定跨越中点的最大子数组的边界，并返回最大子数组中值的和。

FIND-MAX-CROSSING-SUBARRAY（A,low,mid,high）
1 left-sum = -∞
2 sum = 0
3 for i = mid downto low
4     sum = sum + A[i]
5     if sum > left-sum
6        left-sum = sum
7        max-left = i
8 right-sum = -∞
9 sum = 0
10 for j = mid+1 to high
11    sum = sum + A[j]
12    for sum > right-sum
13        right-sum = sum
14        max-right = j
15 return (max-left,max-right,left-sum + right-sum)

        此过程的工作方式如下所述

        第1~7行求出左半部A[low..mid]的最大子数组。由于次子数组必须包含A[mid]， 第3~7行的for循环变量i是从mid开始，递减直到low,因此，它所考察的每个子数组都具有A[i..mid]的形式。第1~2行初始化变量left-sum和sum,前者保存目前位置找到的最大和，后者保存A[i..mid]中所有值的和。每当第5行找到一个子数组A[i..mid]的和大于left-sum时，我们在第6行将left-sum更新为这个子数组的和，并在第7行更新变量max-left来记录当前下标i。

        第8~14行求右半部A[mid+1..high]的最大子数组，过程与左半边类似。此处，第10~14行的for循环的循环变量j是从mid+1开始，递增直到high，因此，它所考察的每个子数组都具有A[mid+1..j]的形式。

        最后，第15行返回下标max-left和max-right，划定跨越中点的最大子数组的边界，并返回子数组A[max-left..max-right]的和left-sum+right-sm.

 FIND-MAXIMUM-SUMARRAY(A,low,high)伪算法

FIND-MAXIMUM-SUBARRAY(A,low,high)
1 if high == low
2   return (low,high,A[low])
3 else mid = [(low+high)/2]
4    (left-low,left-high,left-sum) = FIND-MAXIMUM-SUBARRAY(A,low,mid)
5    (right-low,right-high,right-sum) = FIND-MAXIMUM-SUBARRAY(A,mid+1,high)    
6    (cross-low,cross-high,cross-sum) = FIND-MAX-CROSSING-SUBARRAY(A,low,mid,high)
7    if left-sum ≥ right-sum and left-sum ≥ cross-sum
8        return (left-low,left-high,left-sum)
9    else if right-sum ≥ left-sum and right-sum ≥ cross-sum
10       return (right-low,right-high,right-sum)
11   else return (cross-low,cross-righ,cross-sum)

        初始调用FIND-MAXIMUM-SUBARRAY(A,1,A.length)会求出A[1..n]的最大子数组。 与FIND-MAX-CROSSING-SUBARRAY相似，递归过程FIND-MAXIMUM-SUBARRAY返回一个下标元组，划定了最大子数组的边界，同时返回最大子数组中的值之和。

        第1行测试基本情况，即子数组只有一个元素的情况，在此情况下，子数组只有一个子数组（它自身），因此第2行放回一个下标元组，开始和结束下标均指向唯一的元素，并返回此元素的值作为最大和。

        第3~11行处理递归情况。第3行划分子数组，计算中点下标mid.我们称子数组A[low..mid]为左子数组，A[mid+1..high]为右子数组。因为我们知道子数组A[low..high]至少包含两个元素，则左、右两个子数组各至少包含一个元素。第4行和第5行分别递归地求解左右子数组中的最大子数组。第6~11行完成合并工作。第6行求跨越中点的最大子数组。第7行检测最大和子数组是否在左子数组中，若是，第8行返回此子数组。否则，第9行检测最大和子数组是否在右子数组中，若是，第10行返回此子数组。如果左右子数组均不包含最大子数组，则最大子数组必然跨越中点，第11行将其返回。

C代码实现

注意数组下标从0开始，所以主函数调用FIND_MAXIMUM_SUBARRAY(A,0,length)，low=0 

#include 
#include 

typedef struct max_info{
	int low;
	int high;
	int sum;
}MAX_INFO;
MAX_INFO FIND_MAX_CROSSING_SUBARRAY(int *A, int low, int mid, int high);
MAX_INFO FIND_MAXIMUM_SUBARRAY(int *A, int low, int high);

int main(void)
{
	MAX_INFO max_info = {0};	
	int i = 0;
	int A[] = {13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7};	
	int length=sizeof(A)/sizeof(A[0]);

	max_info = FIND_MAXIMUM_SUBARRAY(A,0,length);
	printf("max_info.low=%d max_info.high=%d max_info.sum=%d\n",max_info.low,max_info.high,max_info.sum);
	for(i = max_info.low; i  <= max_info.high; i++)
		printf("%d ", A[i]);
	printf("\n");

	return 0;
}

MAX_INFO FIND_MAX_CROSSING_SUBARRAY(int *A, int low, int mid, int high)
{
	int left_sum = -10000;
	int right_sum = -10000;
	int sum = 0;
	int max_left = 0;
	int max_right = 0;
	int i = 0;
	int j = 0;
	
	for(i = mid; i >=low; i--)
	{
		sum = sum + A[i];
		if(sum > left_sum)
		{
			left_sum = sum;
			max_left = i;
		}
	}
	sum = 0;
	for(j = mid + 1; j < high; j++)
	{
		sum = sum + A[j];
		if(sum > right_sum)
		{
			right_sum = sum;
			max_right = j;
		}
	}
	MAX_INFO maxinfo = {0};
	maxinfo.low = max_left;
	maxinfo.high = max_right;
	maxinfo.sum = left_sum + right_sum;

	return maxinfo;
}
MAX_INFO FIND_MAXIMUM_SUBARRAY(int *A, int low, int high)
{
	int mid = 0;
	MAX_INFO maxinfo = {0};
	if(low == high){	
		maxinfo.low = low;
		maxinfo.high = high;
		maxinfo.sum = A[low];
		return maxinfo;
	} else {
		MAX_INFO left_info = {0};
		MAX_INFO right_info = {0};
		MAX_INFO cross_info = {0};
		mid = (low+high)/2;
        //左侧最大子数组
		left_info = FIND_MAXIMUM_SUBARRAY(A,low,mid);
        //右侧最大子数组
		right_info = FIND_MAXIMUM_SUBARRAY(A,mid+1,high);
        //跨越中点最大子数组
		cross_info = FIND_MAX_CROSSING_SUBARRAY(A,low,mid,high);
		if(left_info.sum >= right_info.sum && left_info.sum >= cross_info.sum){
			printf("Left: left_info.low=%d left_info.high=%d left_info.sum=%d\n",
				left_info.low,left_info.high,left_info.sum);
			return left_info;
		} else if(right_info.sum >= left_info.sum && right_info.sum >= cross_info.sum) {
			printf("right: right_info.low=%d right_info.high=%d right_info.sum=%d\n",
				right_info.low,right_info.high,right_info.sum);
			return right_info;
		} else {
			printf("cross_info: cross_info.low=%d cross_info.high=%d cross_info.sum=%d\n",
				cross_info.low,cross_info.high,cross_info.sum);
			return cross_info;
		}
	}
}

测试结果 

Left: left_info.low=0 left_info.high=0 left_info.sum=13
Left: left_info.low=0 left_info.high=0 left_info.sum=13
Left: left_info.low=3 left_info.high=3 left_info.sum=20
right: right_info.low=3 right_info.high=3 right_info.sum=20
Left: left_info.low=5 left_info.high=5 left_info.sum=-16
right: right_info.low=8 right_info.high=8 right_info.sum=20
right: right_info.low=8 right_info.high=8 right_info.sum=20
Left: left_info.low=3 left_info.high=3 left_info.sum=20
right: right_info.low=10 right_info.high=10 right_info.sum=12
Left: left_info.low=11 left_info.high=11 left_info.sum=-5
Left: left_info.low=10 left_info.high=10 left_info.sum=12
Left: left_info.low=13 left_info.high=13 left_info.sum=15
Left: left_info.low=15 left_info.high=15 left_info.sum=7
cross_info: cross_info.low=13 cross_info.high=15 cross_info.sum=18
right: right_info.low=13 right_info.high=15 right_info.sum=18
cross_info: cross_info.low=7 cross_info.high=10 cross_info.sum=43
max_info.low=7 max_info.high=10 max_info.sum=43
18 20 -7 12 

    由此，计算出最大子数组为A[7..10]，数组下标从0开始。