第一课 golang数据结构和算法-稀疏数组和队列
第一课 golang数据结构和算法-稀疏数组和队列
tags:
- golang
- 2019尚硅谷
categories:
- golang
- 稀疏数组
- 队列
文章目录
- 第一课 golang数据结构和算法-稀疏数组和队列
-
- 第一节 稀疏sparsearray数组
-
- 1.1 稀疏数组提出
- 1.2 稀疏数组说明
- 1.3 把数组转换为稀疏数组实现
- 1.4 把稀疏数组还原为原数组
- 第二节 队列
-
- 2.1 队列的介绍
- 2.2 数组模拟队列思路-非环形的队列
- 2.3 数组模拟队列代码实现-非环形的队列
- 2.4 数组模拟队列弊端
- 第三节 环形队列-上面队列的优化
-
- 3.1 数组模拟环形队列思路
- 3.2 数组模拟环形队列代码实现
第一节 稀疏sparsearray数组
1.1 稀疏数组提出
- 编写的五子棋程序中，有存盘退出和续上盘的功能
- 因为该二维数组的很多值是默认值0，因此记录了很多没有意义的数据
- 当一个数组中大部分元素为0，或者为同一个值的数组时，可以使用稀疏数组来保存该数组。
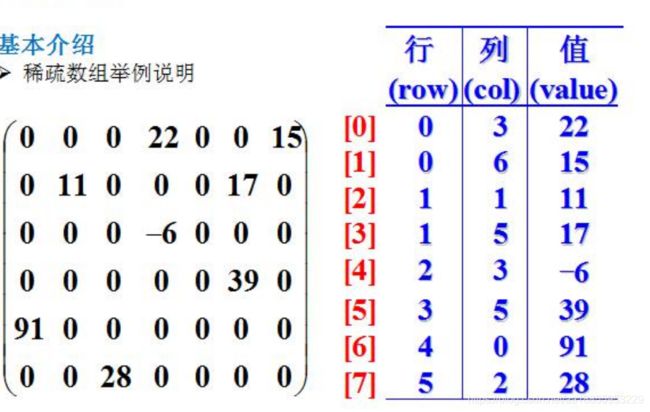
1.2 稀疏数组说明
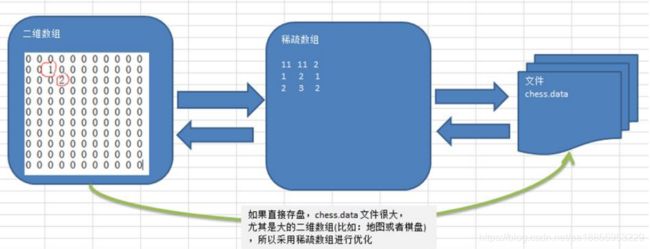
- 稀疏数组的处理方法是:
- 记录数组一共有几行几列，有多少个不同的值
- 思想:把具有不同值的元素的行列及值记录在一个小规模的数组中，从而缩小程序的规模
- 使用稀疏数组，来保留类似前面的二维数组(棋盘、地图等等)
- 把稀疏数组存盘，并且可以从新恢复原来的二维数组数
1.3 把数组转换为稀疏数组实现
package main
import (
"fmt"
"bufio"
"os"
)
type ValNode struct{
row int
col int
val int
}
func main(){
filePath := "d:/sparsearray.data"
file, err := os.OpenFile(filePath, os.O_WRONLY|os.O_CREATE, 0666)
if err!=nil{
fmt.Printf("open file err=%v\n", err)
return
}
//及时关闭file句柄
defer file.Close()
// 1. 创建一个原始数组
var chessMap [11][11]int
chessMap[1][2] = 1
chessMap[2][3] = 2
// 2. 输出查看原始数组
for _, v := range chessMap {
for _, v2 := range v {
fmt.Printf("%d\t", v2)
}
fmt.Println()
}
// 3. 转成稀疏数组
//思路
//(1)．遍历chessMap，如果我们发现有一个元素的值不为0，创建一个node结构体
//(2)．将其放入到对应的切片即可
var sparseArr []ValNode
// 添加初始节点 保存二维数组规模(行和列, 默认值)
ValNode := ValNode{
row : 11,
col : 11,
val : 0,
}
sparseArr = append(sparseArr, ValNode)
for i, v := range chessMap{
for j, v1 := range v{
if v1 != 0{
// 创建一个ValNode 值节点
ValNode.row = i
ValNode.col = j
ValNode.val = v1
sparseArr = append(sparseArr, ValNode)
}
}
}
// 4. 输出稀疏数组
fmt.Println("当前的稀疏数组是:")
writer := bufio.NewWriter(file)
for _, ValNode := range sparseArr{
var s1 = fmt.Sprintf("%d %d %d\n", ValNode.row, ValNode.col, ValNode.val)
writer.WriteString(s1)
fmt.Printf("%s", s1)
}
writer.Flush()
}
1.4 把稀疏数组还原为原数组
- 坑点一：读取后是字符串需要，分割成字符串数组，这里通过Split但是数组最后一个多一个换行符号需要去掉。
- 坑点二：golang是无法直接在二维数组创建时传变量的。这个时候先声明一个二维切片。初始化二维切片后。填入初始值。
package main
import (
"fmt"
"os"
"bufio"
"io"
"strings"
"strconv"
)
func main(){
file, err := os.Open("d:/sparsearray.data")
if err != nil{
fmt.Printf("打开文件出错:%v", err)
}
defer file.Close()
reader := bufio.NewReader(file)
str, err := reader.ReadString('\n')
if err == io.EOF{ //io.EOF 文件末尾
fmt.Println("第一行 读取完毕")
}
// 分割字符串 通过空格
arr := strings.Split(str, " ")
m, err := strconv.Atoi(arr[0])
n, err := strconv.Atoi(arr[1])
v, err := strconv.Atoi(strings.Replace(arr[2], "\n", "", -1))
if err != nil {
// handle error
fmt.Println(err)
os.Exit(2)
}
// golang是无法直接在二维数组创建时传变量的 var chessMap [m][n]int 不能成功
var chessMap [][]int
for i := 0; i < m; i++ {
arr1 := make([]int, n) //创建一个一维切片
chessMap = append(chessMap, arr1) //把一维切片,当作一个整体传入二维切片中
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
chessMap[i][j] = v
}
}
for {
str, err := reader.ReadString('\n') // 一次读到换行结束
if err == io.EOF{ //io.EOF 文件末尾
break
}
//输出内容
arr := strings.Split(str, " ")
m, err := strconv.Atoi(arr[0])
n, err := strconv.Atoi(arr[1])
v, err := strconv.Atoi(strings.Replace(arr[2], "\n", "", -1))
chessMap[m][n] = v
}
fmt.Println("稀疏数组还原成原数组。。。")
for _, v := range chessMap {
for _, v2 := range v {
fmt.Printf("%d\t", v2)
}
fmt.Println()
}
}
第二节 队列
2.1 队列的介绍
- 队列是一个有序列表，可以用数组或是链表来实现。
- 遵循先入先出的原则。即:先存入队列的数据，要先取出。后存入的要后取出
- 示意图:(使用数组模拟队列示意图)
2.2 数组模拟队列思路-非环形的队列
-
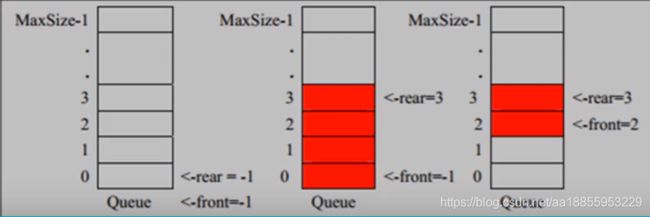
队列本身是有序列表，若使用数组的结构来存储队列的数据，则队列数组的声明如下其maxSize是该队列的最大容量。
-
因为队列的输出、输入是分别从前后端来处理，因此需要两个变量front及rear分别记录队列前后端的下标，front会随着数据输出而改变，而rear则是随着数据输入而改变，如下图所示：
-
当我们将数据存入队列时称为”addqueue"，addqueue的处理需要有两个步骤:
- 将尾指针往后移:rear+1 , front == rear时队列是空的
- 若尾指引rear小于等于队列的最大下标 MaxSize-1，则将数据存入rear所指的数组元素中，否则无法存入数据。rear == MaxSize -1[队列满]
2.3 数组模拟队列代码实现-非环形的队列
package main
import (
"fmt"
"errors"
"os"
)
// 使用一个结构体管理队列
type Queue struct{
maxSize int
array [5]int // 数组=>模拟队列
front int //表示指向队列首
rear int //表示指向队列的尾部
}
// 添加数据到队列
func (this *Queue) AddQueue(val int) (err error){
// 判断队列是否已经满了
if this.rear == this.maxSize -1 { // rear包含队列尾部
return errors.New("队列已满")
}
this.rear++ // rear后移
this.array[this.rear] = val
return
}
func (this *Queue) GetQueue() (val int, err error){
// 先判断队列是否已满
if this.rear == this.front{ // 队空
return -1, errors.New("queue empty")
}
this.front++
val = this.array[this.front]
return val, err
}
// 显示队列 找到队首 遍历到队尾
func (this *Queue) ShowQueue(){
fmt.Println("队列当前的情况是:")
// 队首不包含队首元素
for i := this.front + 1; i <= this.rear; i++{
fmt.Printf("array[%d]=%d\n", i, this.array[i])
}
fmt.Println()
}
// 编写主函数
func main(){
// 先创建一个队列
var queue = &Queue{
maxSize : 5,
front : -1,
rear : -1,
}
var key string
var val int
for {
fmt.Println("1. 输入add 添加元素到队列")
fmt.Println("2. 输入get 从队列中获取元素")
fmt.Println("3. 输入show 显示队列中的元素")
fmt.Println("4. 输入exit 退出程序")
fmt.Scanln(&key)
switch key {
case "add":
fmt.Println("输入数据入队")
fmt.Scanln(&val)
err := queue.AddQueue(val)
if err != nil {
fmt.Println(err.Error())
}else{
fmt.Println("加入队列ok")
}
case "get":
val, err := queue.GetQueue()
if err != nil{
fmt.Println(err.Error())
} else {
fmt.Println("从队列中取出数据：", val)
}
case "show":
queue.ShowQueue()
case "exit":
os.Exit(0)
}
}
}
2.4 数组模拟队列弊端
- 上面代码实现了基本队列结构，但是没有有效的利用数组空间，队列只能使用一次。
- 请思考，如何使用数组实现一个环形的队列(通过取模的方式改进)
第三节 环形队列-上面队列的优化
3.1 数组模拟环形队列思路
- 尾索引的下一个为头索引时表示队列满，即将队列容量空出一个作为约定,这个在做判断队列满的时候需要注意(tail+1) % maxSize == head [满]
- tail == head [空]
- 分析思路:
- 什么时候表示队列满(tail+1) % maxSize = head
- tail ==head 表示空
- 初始化时，tail= 0 head= 0
- 怎么统计该队列有多少个元素被取出(tail + maxSize - head ) % maxSize
3.2 数组模拟环形队列代码实现
package main
import (
"fmt"
"errors"
"os"
)
// 使用一个结构体管理环形队列
type CircleQueue struct{
maxSize int // 4
array [5]int // 数组
head int // 指向队列的头部
tail int // 指向队列的尾部
}
// 入队列 AddQueue(push) GetQueue(pop)
func (this *CircleQueue) Push(val int) (err error) {
if this.IsFull(){
return errors.New("queue full")
}
// 分析出this.tail 在队列尾部 不包含最后的元素
this.array[this.tail] = val // 把值给尾部
// 这里要注意虽然数组容量是5 实际上队列最多只能存四个 因为下面这句话
this.tail = (this.tail + 1) % this.maxSize
return
}
// 出队列
func (this *CircleQueue) Pop() (val int, err error) {
if this.IsEmpty(){
return 0, errors.New("queue empty")
}
// 取出, head 是指向队首 并且含队首元素
val = this.array[this.head]
this.head = (this.head + 1) % this.maxSize
return val, err
}
// 显示队列
func (this *CircleQueue) ListQueue(){
fmt.Println("环形队列的情况如下:")
// 取出当前队列有多少个元素
size := this.Size()
if size == 0{
fmt.Println("队列为空")
}
// 设计一个辅助变量. 指向head
tempHead := this.head
for i := 0; i < size; i++{
fmt.Printf("arr[%d]=%d\t", tempHead, this.array[tempHead])
tempHead = (tempHead + 1) % this.maxSize
}
fmt.Println()
}
// 判断环形队列为满
func (this *CircleQueue) IsFull() bool{
return (this.tail + 1) % this.maxSize == this.head
}
// 判断环形队列为空
func (this *CircleQueue) IsEmpty() bool{
return this.tail == this.head
}
// 取出环形队列有多少个元素
func (this *CircleQueue) Size() int{
return (this.tail + this.maxSize - this.head) % this.maxSize
}
// 编写主函数
func main(){
// 先创建一个环形队列
var queue = &CircleQueue{
maxSize : 5,
head : 0,
tail : 0,
}
var key string
var val int
for {
fmt.Println("1. 输入add 添加元素到队列")
fmt.Println("2. 输入get 从队列中获取元素")
fmt.Println("3. 输入show 显示队列中的元素")
fmt.Println("4. 输入exit 退出程序")
fmt.Scanln(&key)
switch key {
case "add":
fmt.Println("输入数据入队")
fmt.Scanln(&val)
err := queue.Push(val)
if err != nil {
fmt.Println(err.Error())
}else{
fmt.Println("加入队列ok")
}
case "get":
val, err := queue.Pop()
if err != nil{
fmt.Println(err.Error())
} else {
fmt.Println("从队列中取出数据：", val)
}
case "show":
queue.ListQueue()
case "exit":
os.Exit(0)
}
}
}