python进阶（数据分析numpy库 二）

   2、ndarray数组的切片：

    （1）数组切片的基本知识

•             各个维度上单独切片，用 “，” 隔开，用 “：”表示该维度切片（切片不需要加[ ] --- 例：
•                  arr1[np.ix_([1,3],1:4)]，零碎的行需要加[ ] ------- 例：arr1[[1,3,4]]）。
•             数组切片获得的 新数组与原数据组共用一个  内存空间，切片数组更改数据原数组也会更改。
•            ndarray 的切片与列表方式切片有一些区别，尽量用数组方式。

import numpy as np
list1 = [
  [ [1,2,3],
    [3,2,1]],

  [ [4,5,6],
    [6,5,4]],

  [ [7,8,9],
    [9,8,7]]]
arr1 = np.array(list1)

          （一）数组切片与列表方式切片的区别：

print(arr1[1,:,1:3])  
数组切片：
[[5 6]
 [5 4]]
print(arr1[1][:][1:3])
列表方式：
[[6 5 4]]

           （二）数组切片用法：

           切第二行的元素
print(arr1[1,:,:])
print(arr1[1])
           
print(arr1[1,:,1:3])
[[5 6]
 [5 4]]

      （2）切片数组赋值列表或数组：

赋值列表
import numpy as np
arr1 = np.random.randint(1,9,(3,4))
arr1[:,::2] = [100,100]
print(arr1) 

  [[100   6 100   2]
 [100   6 100   1]
 [100   3 100   5]]

赋值数组
import numpy as np
arr1 = np.random.randint(1,9,(3,12))
arr1[:,::2] = np.array([100,100,100,100,100,100])
print(arr1)

[[100   4 100   3 100   5 100   7 100   8 100   8]
 [100   2 100   1 100   3 100   8 100   3 100   1]
 [100   6 100   1 100   1 100   6 100   8 100   2]]

     （3）... 在numpy索引中的用法 【 [..., : -1] 】

1、当数组的 ndim 比较高或者ndim 不确定时，我们使用切片可以使用 ... 来代替其他维度所有内容
    eg：array[0:405,0:405,...]     ---- 切片取出 前405行，前405列其他维度所有的数据
    eg：array[...,3:10]     ---- 切片，前面的维度都要，仅仅在最后一个维度切 3-9

     （4） numpy 切片快速颠倒数组 【 [::-1] ，[::-2]  ...  】

arr1 = [1,2,3,4]
arr2 = arr[::-1]    # arr2 = [4,3,2,1]

arr2 = arr[::-2]    # arr2 = [4,2] # 数组颠倒，步长为2

     （5）花式索引（np.ix_()）：用整数数组进行索引。

               注意 内部函数  .ix_( 索引数组1，索引数组2  ) 的用法。

               也可用转置（ .T ）来取与 .ix_(）方法一样的结果。

import numpy as np
arr1 = np.arange(1,31,1).reshape(6,5)
print(arr1)
# 获得第 2 4 5 行的所有元素 
====================================== 取多行数据 =======
print(arr1[[1,3,4]])      ----- 这里要区分 与  print(arr1[1,3,4]) 的区别
=======================================================================
# 注意这里取的是 （1,1） （3,2） （4,4） 四个元素
print(arr1[[1,3,4],[1,2,4]])
==================================== np.ix_()用法 =======================
# 取得时是所有 第 2 4 5 行 与 1,2,4列的元素。 用 内部函数  np.ix_( 索引数组1，索引数组2  )
print(arr1[np.ix_([1,3,4],[1,2,4])])
# 也可以用转置 来取，与 np.ix_( )结果相同。
print(arr1[[1,3,4]].T[[1,2,4]].T)

     （6）bool值数组索引：

•             特点: ① 利用布尔类型的数组进行数据索引，最终返回的结果是对应索引数组中数据为True位置的值。
•                      ② 利用bool 索引替换和修改 数组的值 , 例： arr1[arr1 == ' tom'] = 'jerry'  ------ bool 索引改值
•                      ③ bool索引的逻辑运算符 & | ~ ,numpy中不能用 or and not

实例用法：  

    ①  

求数组 数 > 5 的所有数。
import numpy as np
arr1 = np.arange(1,11,1).reshape(2,5)
# [[ 1  2  3  4  5]
#  [ 6  7  8  9 10]]
print(arr1 > 5)
# [[False False False False False]
#  [ True  True  True  True  True]]
print(arr1[arr1 > 5])
# [ 6  7  8  9 10]

    ②

            

names = np.array(['joe','tom','anne'])
scores = np.array([[70,80,90],
                   [77,88,91],
                   [80,90,70]])
classes = np.array(['语文','数学','英语'])
# 输出 joe 的成绩
bool_1 = names == 'joe'
print(bool_1)                              [ True False False]
print(scores[bool_1])        #  [[70 80 90]]
# 输出joe的数学成绩
bool_2 = classes == '数学'
print(bool_2)                              [False  True False]
print(scores[bool_1,bool_2])   # [80]
# 第三题
print(scores[(names == 'joe')|(names == 'anne')]) 
# [[70 80 90]
#  [80 90 70]]
#第四题
print(scores[(names != 'joe') & (names != 'anne')])  # [[77 88 91]]

   3、ndarray-数组转置与轴对换：

•                 特点: ① 注意数组转置与  reshape（）的区别。
•                           ② 数组转置是指将shape进行重置操作，原始的shape值为：(2,3,4)，转置后shape的值为：(4,3,2)。
•                                 可以通过调用数组的对象.transpose（  ）函数或者对象.T 属性进行数组转置操作。
•                           ③ .T 与 .transpose（  ）返回值(用变量接收)是修改数据, 原数据不变 , 转置是一个视图 

      ① 数组的转置：

import numpy as np
arr1 = np.arange(1,11,1).reshape(2,5)
1、 利用 T 属性
arr2 = arr1.T
print(arr2)
2、利用 transpose（）函数 
arr3 = arr1.transpose()
print(arr3)
      

      ② 数组的轴对换：

import numpy as np
arr1 = np.arange(1,13,1).reshape(2,3,2)
arr2 = arr1.transpose(2,0,1)     中间不用加小（）
print(arr2)
[[[ 1  3  5]
  [ 7  9 11]]

 [[ 2  4  6]
  [ 8 10 12]]]

            运行过程：

  4、ndarray-数组拉伸与合并:

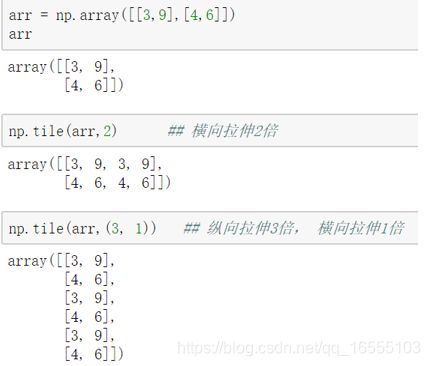
       ①数组的拉伸：np.tile（A，rep）：

                    可以将数组A进行拉伸，沿着A的维度重复rep次

例子：

import numpy as np
arr1 = np.array([[1,2,3],
                 [4,5,6]])
print(np.tile(arr1,3))        # 一个数字为 横向拉伸 3 倍
print(np.tile(arr1,(3,2)))    # 纵向 拉伸 3倍 ，横向拉伸 2倍
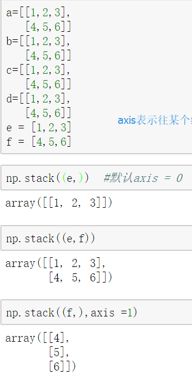
print(np.tile(arr1,(3,2,1)))    #  0轴 拉伸 3倍 ，1轴 拉伸 2倍,2轴拉伸 1倍

       ② 数组的合并：np.stack（）函数 

               对于ndarray数组而言，多个数组可以执行合并操作，合并的方式有多种：

•                Stack(arrays,axis=0):沿着新的轴加入一个维度   （   axis是坐标轴 ，stack 堆 ）
•                vstack（）：堆栈数组垂直顺序（行）,不会增加维度  -------- vartical  垂直                 
•                hstack（）：堆栈数组水平顺序（列）,不会增加维度 。
•                stack（）函数内部要加 小 （）。
•                         堆叠 :  https://blog.csdn.net/u013019431/article/details/79768219

• import numpy as np
  a = np.array([[1,2,3],
              [4,5,6]])
  b = np.array([[1,2,3],
              [4,5,6]])
  c = np.array([[1,2,3],
              [4,5,6]])
  d = np.array([[1,2,3],
              [4,5,6]])
  e = np.array([1,2,3])
  f = np.array([4,5,6])
  print(np.stack((e,)))   # 注意 ： stack 里面要用小（）括起来，默认 axis 为 0 轴。
  print(np.stack((e,),axis=1))
  print(np.stack((e,f),axis=1))

                        

八、ndarray-通用函数/常用函数:（元素级运算）

          ufunc：接受一个或多个标量值，进行快速元素级运算的函数，主要包括一元函数和二元函数。

     1、一元 ufunc：

            元素级操作，调用方法： np . 函数名（）。

 

 

 例子：

 

    2、二元ufunc ：

     3、常用的函数实例

        (1)  聚合函数

arr23 = np.arange(6).reshape((2, 3))
print(arr23)
print(arr23.sum(axis=0))
print(arr23.mean())
print(np.average(range(1,11), weights=range(10,0,-1)))    # 加权均值
print(arr23.std())
print(arr23.var())    # 方差
print(arr23.argmax(axis=0))
print(arr23.argmin(axis=1))
print(arr23.cumsum()) 

answer：
[[0 1 2]
 [3 4 5]]
[3 5 7]
2.5
1.707825127659933
2.9166666666666665
[1 1 1]
[0 0]
[ 0  1  3  6 10 15]

    （2）拉伸 np.tail  与 重复函数 np.repeat 区别

arr21 = np.ndarry([2,3,4])
print(np.tile(arr21, 5))          ------ [2 3 4 2 3 4 2 3 4 2 3 4 2 3 4]
print(np.repeat(arr21, [3, 2, 1]))   ------- [2 2 2 3 3 4]

arr23 = np.arange(6).reshape((2, 3))
print(arr23)
print(np.repeat(arr23, 2, axis=1))
print(np.repeat(arr23, 2, axis=0))

print(np.tile(arr23, 2))
print(np.tile(arr23, 2))

[[0 1 2]
 [3 4 5]]
[[0 0 1 1 2 2]
 [3 3 4 4 5 5]]
[[0 1 2]
 [0 1 2]
 [3 4 5]
 [3 4 5]]
[[0 1 2 0 1 2]
 [3 4 5 3 4 5]]
[[0 1 2 0 1 2]
 [3 4 5 3 4 5]]

    （3）np. where()函数(三元表达式x if condition else y效果)：

                  np.where(condition,arr1,arr2)   满足条件 选择arr1，不满足 选择arr2

用法：

   （4）去重函数   np.unique(对象)：

# 几个重要函数
arr22 = np.array([3, 4, 2, 1, 1, 3, 2, 4])

print(np.unique(arr22))

[1 2 3 4]

    （5）排序 sorted  sort  argsort 区别

arr21 = np.array([4, 3, 2])

print(sorted(arr21))  # 返回临时排序的列表
print(arr21)  # 原数组

print(arr21.argsort())  # 排序后的初始下标

[2, 3, 4]
[4 3 2]
[2 1 0]

arr21.sort()  # 不返回值，只进行排序操作
print(arr21)  # 排序后数组

[2 3 4]

   （6）Python numpy 数组 左右反转/上下反转

numpy API:

flattened
flip() (in module numpy)      
fliplr() (in module numpy)     # 二维数组  左右反转
flipud() (in module numpy)     

   （8）扁平化操作

1、数据对象.flat
2、数据对象.shape = (-1,)
3、数据对象.real()
4、数据对象.reshape(-1)
print(a3.ravel())   # 不改变源数据
print(a3.flatten("C"))
print(a3.flatten("F"))

     (9)  逻辑 与  或 运算

arr12 = np.array([True, True, False])
arr13 = np.array([True, True, True])
arr14 = np.array([False, False, False])

print(np.any(arr12))
print(np.any(arr14))

print(np.all(arr12))
print(np.all(arr13))

True
False
False
True

    （10）查看帮助函数：help( )

help(np.log)   -------- 查看对数函数的用法

九、数据数据文件存储于读取

     1、数组数据二进制存储与读取：

              1.1、数组二进制存储：np.save() 

              1.2、数组二进制读取：np.load()

     2、数组数据文本存储与读取：

              2.1、数组文本文件存储：

•                 特点：① 存储为文本文件是一定要转化为二维数组结构，否则报错

                            ① np.savetxt() ：

                            ② np.genfromtxt() ：

              2.2、数组文本文件读取：np.loadtxt()

                 

十、numpy中的逻辑运算符

•              bool索引的逻辑运算符 & | ~ ,numpy中不能用 or and not

 

十一、numpy其他用法

  （1）numpy数据类型转化为矩阵

•    求矩阵的逆矩阵

求矩阵的逆：
    ① numpy.linalg.inv(X)   前提：X 必须是一个 矩阵（matrix） 的数据类型
    ② xxx.I                 前提：xxx 必须是一个 矩阵（matrix） 的数据类型
-------------------------------------------------------------------------------------------
# 求矩阵的逆
import numpy as np
a = [
    [1],
    [2]
    ]
a=np.mat(a)          -------------- 生成一个矩阵的数据类型
print(type(a))
b=np.linalg.inv(a)  ------------ 或者 b = a.I（前提：数据类型必须是matrix数据类型，不能使ndarray类型）
print(b)

求解：numpy.linalg.solve()

•    求矩阵的特征向量和特征值、SVD矩阵分解

SVD矩阵分解：    np.linalg.svd(二维数组)
 eg：   u,singma,v = np.linalg.svd(二维数组)       ------ u,singma,v 接收分解后的三个矩阵。

 

•    numpy的矩阵数据类型之间的计算方式

numpy ndarray的数据类型：矩阵 A 矩阵 B    
--------------------------------------------------------------------------------------- 
A*B   >>>>>>> 对应元素相乘（元素级操作）
np.dot(A,B)  >>>>>> 矩阵A与矩阵B的点积
=============================================================================================
numpy 矩阵（matrix）的数据类型：矩阵 A 矩阵 B 
A*B   >>>>>>> 直接结果就是 点积

       A是矩阵数据类型，则  是   A的转置 * A

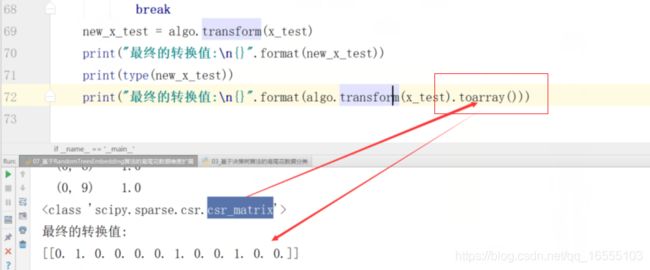
  （2）稀疏矩阵与普通数组矩阵： . toarray()

   （3）数组的扁平化：

1、数据对象.flat
2、数据对象.shape = (-1,)
3、数据对象.real()
4、数据对象.reshape(-1)

   （4） Python numpy 数组 左右反转/上下反转

numpy API:

flattened
flip() (in module numpy)      
fliplr() (in module numpy)     # 二维数组  左右反转
flipud() (in module numpy)     

flip:
flip(m, 0) is equivalent to flipud(m).

flip(m, 1) is equivalent to fliplr(m).

flip(m, n) corresponds to m[...,::-1,...] with ::-1 at position n.

flip(m) corresponds to m[::-1,::-1,...,::-1] with ::-1 at all positions.

flip(m, (0, 1)) corresponds to m[::-1,::-1,...] with ::-1 at position 0 and position 1.

>>> A = np.arange(8).reshape((2,2,2))
>>> A
array([[[0, 1],
        [2, 3]],
       [[4, 5],
        [6, 7]]])
>>> flip(A, 0)
array([[[4, 5],
        [6, 7]],
       [[0, 1],
        [2, 3]]])
>>> flip(A, 1)
array([[[2, 3],
        [0, 1]],
       [[6, 7],
        [4, 5]]])
>>> np.flip(A)
array([[[7, 6],
        [5, 4]],
       [[3, 2],
        [1, 0]]])
>>> np.flip(A, (0, 2))
array([[[5, 4],
        [7, 6]],
       [[1, 0],
        [3, 2]]])
>>> A = np.random.randn(3,4,5)
>>> np.all(flip(A,2) == A[:,:,::-1,...])
True

 

flipud: (==flip(m, 1) )
Flip array in the up/down direction.

Flip the entries in each column in the up/down direction. Rows are preserved, but appear in a different order than before.

Equivalent to m[::-1,...]. Does not require the array to be two-dimensional.

 

>>> A = np.diag([1.0, 2, 3])
>>> A
array([[ 1.,  0.,  0.],
       [ 0.,  2.,  0.],
       [ 0.,  0.,  3.]])
>>> np.flipud(A)
array([[ 0.,  0.,  3.],
       [ 0.,  2.,  0.],
       [ 1.,  0.,  0.]])
>>>
>>> A = np.random.randn(2,3,5)
>>> np.all(np.flipud(A) == A[::-1,...])
True
>>>
>>> np.flipud([1,2])
array([2, 1])

fliplr: (==flip(m, 0))
　　Equivalent to m[:,::-1]. Requires the array to be at least 2-D.

        Flip array in the left/right direction.
    rot90
        Rotate array counterclockwise.

>>> A = np.diag([1.,2.,3.])
>>> A
array([[ 1.,  0.,  0.],
       [ 0.,  2.,  0.],
       [ 0.,  0.,  3.]])
>>> np.fliplr(A)
array([[ 0.,  0.,  1.],
       [ 0.,  2.,  0.],
       [ 3.,  0.,  0.]])
>>>
>>> A = np.random.randn(2,3,5)
>>> np.all(np.fliplr(A) == A[:,::-1,...])
True