leetcode刷题记录-正则表达式匹配
leetcode刷题记录
题目 正则表达式匹配
题目描述
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 示例 1： 输入：nums1 = [1,3], nums2 = [2] 输出：2.00000 解释：合并数组 = [1,2,3] ，中位数 2 示例 2： 输入：nums1 = [1,2], nums2 = [3,4] 输出：2.50000 解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5 示例 3： 输入：nums1 = [0,0], nums2 = [0,0] 输出：0.00000 示例 4： 输入：nums1 = [], nums2 = [1] 输出：1.00000 示例 5： 输入：nums1 = [2], nums2 = [] 输出：2.00000
提示：
nums1.length == m
nums2.length == n
0 <= m <= 1000 0 <= n <= 1000
1 <= m + n <= 2000 -10^6 <= nums1[i], nums2[i] <= 10^6
链接: leetcode地址
思路
给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘’ 的正则表达式匹配。 ‘.’ 匹配任意单个字符 ‘’ 匹配零个或多个前面的那一个元素 所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。 示例 1： 输入：s = “aa” p = “a” 输出：false 解释：“a” 无法匹配 “aa” 整个字符串。 示例 2: 输入：s = “aa” p = “a*” 输出：true 解释：因为 ‘’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此，字符串 “aa” 可被视为 ‘a’ 重复了一次。 示例 3： 输入：s = “ab” p = ". " 输出：true 解释：".* " 表示可匹配零个或多个（’‘）任意字符（’.'）。 示例 4： 输入：s = “aab” p = “c * a * b” 输出：true 解释：因为 '’ 表示零个或多个，这里 ‘c’ 为 0 个, ‘a’ 被重复一次。因此可以匹配字符串 “aab”。 示例 5： 输入：s = “mississippi” p = “misisp*.” 输出：false 提示： 0 <= s.length <= 20 0 <= p.length <= 30 s 可能为空，且只包含从 a-z 的小写字母。 p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 。 保证每次出现字符 * 时，前面都匹配到有效的字符
题意
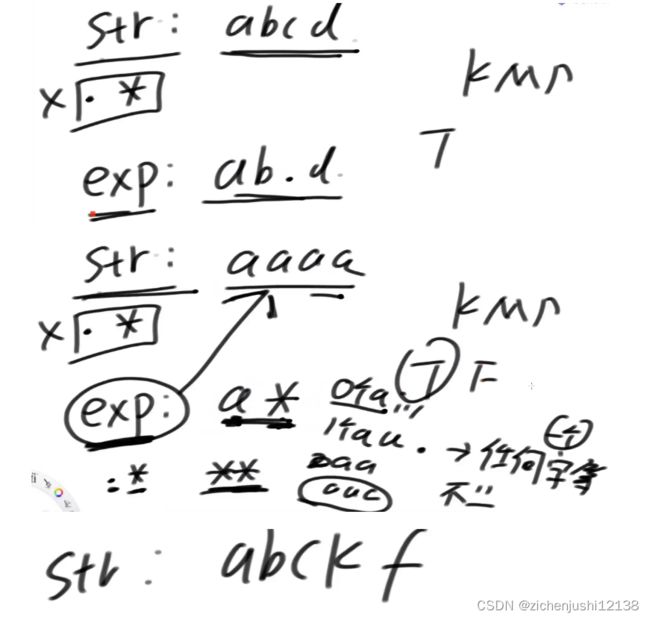
str一定不含有.
表达式串能不能搞成str
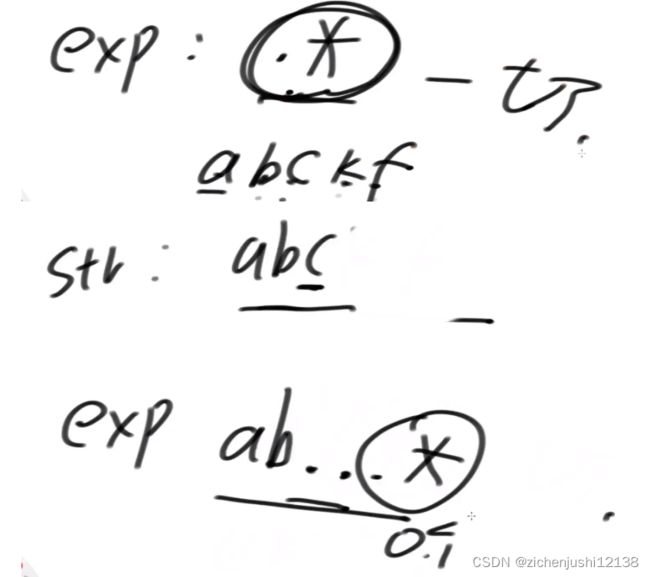
题解
样本对应模型
定义二维表
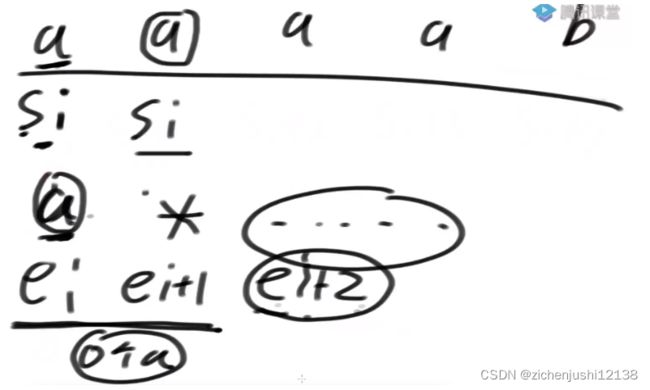
dp【i】:
str从i出发到后面的所有，能不能被表达式串从j出发到后面的所有配出来，
它俩之前的死去根本就不管
大过滤
str不能有. 和 *
exp 开头不能是, 两个不能挨着
public static boolean isValid(char[] s, char[] e) {
// s中不能有'.' or '*'
for (int i = 0; i < s.length; i++) {
if (s[i] == '*' || s[i] == '.') {
return false;
}
}
// 开头的e[0]不能是'*'，没有相邻的'*'
for (int i = 0; i < e.length; i++) {
if (e[i] == '*' && (i == 0 || e[i - 1] == '*')) {
return false;
}
}
return true;
}
递归含义:
str从si出发及其后面的所有, 能不能被 exp从ei出发及其后面的所有配出来
能配出来返回true, 否则false
逻辑划分: ei下一个位置是不是*
- ei下一个位置不是*
如果ei+1不是，就说明我ei没有操作空间了。它不能指望后面的把它变没, 代表此时si必须能和ei对上
只能是 [ei]字符等于[si]字符
要么 [ei]字符是 . , 它能够变成一切
- ei+1是*
ei跟si不相等, 只能让ei+1*把ei字符变成0个
相等的时候
0) 变零个
让a* 变0个a, 后面去匹配
-
变1个a
-
变两个a
-
3个a
-
4个a
所以每一种分支全都走，但有一个走通，直接返回true，所有分支都走不通，返回false，
代码
ei + 1位置是*
ei是c, 不进while
ei是a, 进while
变0个
变1个
…
最后一步跳出while, 尝试4个a的时候
public static boolean isValid(char[] s, char[] e) {
// s中不能有'.' or '*'
for (int i = 0; i < s.length; i++) {
if (s[i] == '*' || s[i] == '.') {
return false;
}
}
// 开头的e[0]不能是'*'，没有相邻的'*'
for (int i = 0; i < e.length; i++) {
if (e[i] == '*' && (i == 0 || e[i - 1] == '*')) {
return false;
}
}
return true;
}
// 初始尝试版本，不包含斜率优化
public static boolean isMatch1(String str, String exp) {
if (str == null || exp == null) {
return false;
}
char[] s = str.toCharArray();
char[] e = exp.toCharArray();
return isValid(s, e) && process(s, e, 0, 0);
}
// str[si.....] 能不能被 exp[ei.....]配出来！ true false
public static boolean process(char[] s, char[] e, int si, int ei) {
if (ei == e.length) { // exp 没了 str？
return si == s.length;
}
// exp[ei]还有字符
// ei + 1位置的字符，不是*
if (ei + 1 == e.length || e[ei + 1] != '*') {
// ei + 1 不是*
// str[si] 必须和 exp[ei] 能配上！
return si != s.length && (e[ei] == s[si] || e[ei] == '.') && process(s, e, si + 1, ei + 1);
}
// exp[ei]还有字符
// ei + 1位置的字符，是*!
while (si != s.length && (e[ei] == s[si] || e[ei] == '.')) {
if (process(s, e, si, ei + 2)) {
return true;
}
si++;
}
return process(s, e, si, ei + 2);
}
记忆化搜索
// 改记忆化搜索+斜率优化
public static boolean isMatch2(String str, String exp) {
if (str == null || exp == null) {
return false;
}
char[] s = str.toCharArray();
char[] e = exp.toCharArray();
if (!isValid(s, e)) {
return false;
}
int[][] dp = new int[s.length + 1][e.length + 1];
// dp[i][j] = 0, 没算过！
// dp[i][j] = -1 算过，返回值是false
// dp[i][j] = 1 算过，返回值是true
return isValid(s, e) && process2(s, e, 0, 0, dp);
}
public static boolean process2(char[] s, char[] e, int si, int ei, int[][] dp) {
if (dp[si][ei] != 0) {
return dp[si][ei] == 1;
}
boolean ans = false;
if (ei == e.length) {
ans = si == s.length;
} else {
if (ei + 1 == e.length || e[ei + 1] != '*') {
ans = si != s.length && (e[ei] == s[si] || e[ei] == '.') && process2(s, e, si + 1, ei + 1, dp);
} else {
if (si == s.length) { // ei ei+1 *
ans = process2(s, e, si, ei + 2, dp);
} else { // si没结束
if (s[si] != e[ei] && e[ei] != '.') {
ans = process2(s, e, si, ei + 2, dp);
} else { // s[si] 可以和 e[ei]配上
ans = process2(s, e, si, ei + 2, dp) || process2(s, e, si + 1, ei, dp);
}
}
}
}
dp[si][ei] = ans ? 1 : -1;
return ans;
}
优化
斜率优化, 省掉while
f(13, 29)的依赖
f(12, 29)的依赖
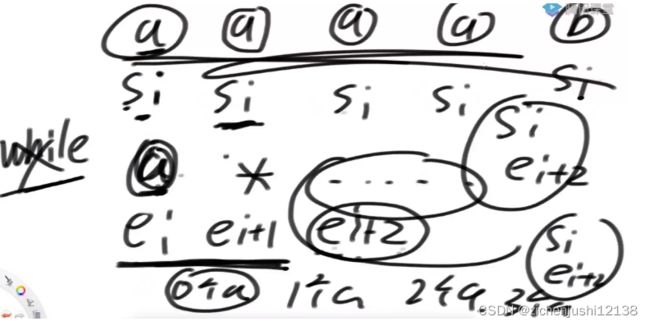
在str中i位置字符和str中i+1位置字符它一样的时候就存在这个优化
例子
14开始的状态没有13开始的大
代码
当我一个格子有枚举行为的时候，我就观察他已经算过的格子，能不能把枚举行为替代掉，
从而得到一个使用有限若干个位置的方式来得到这一个格子的值
斜率优化时, 不能配上通项公式也是一样的
代码
// 动态规划版本 + 斜率优化
public static boolean isMatch3(String str, String pattern) {
if (str == null || pattern == null) {
return false;
}
char[] s = str.toCharArray();
char[] p = pattern.toCharArray();
if (!isValid(s, p)) {
return false;
}
int N = s.length;
int M = p.length;
boolean[][] dp = new boolean[N + 1][M + 1];
dp[N][M] = true;
for (int j = M - 1; j >= 0; j--) {
dp[N][j] = (j + 1 < M && p[j + 1] == '*') && dp[N][j + 2];
}
// dp[0..N-2][M-1]都等于false，只有dp[N-1][M-1]需要讨论
if (N > 0 && M > 0) {
dp[N - 1][M - 1] = (s[N - 1] == p[M - 1] || p[M - 1] == '.');
}
for (int i = N - 1; i >= 0; i--) {
for (int j = M - 2; j >= 0; j--) {
if (p[j + 1] != '*') {
dp[i][j] = ((s[i] == p[j]) || (p[j] == '.')) && dp[i + 1][j + 1];
} else {
if ((s[i] == p[j] || p[j] == '.') && dp[i + 1][j]) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i][j + 2];
}
}
}
}
return dp[0][0];
}
一般 将 尝试改成记忆化搜索就可以过了