CNN入门及详解

CNN(卷积神经网络)详解

CNN有三个几本思想，局部感受野(local receptive fields) 权值共享(shared weights) 池化(pooling)

DNN全连接神经网络另学

下面是一个三个hidden layer的网络结构图

盗图1

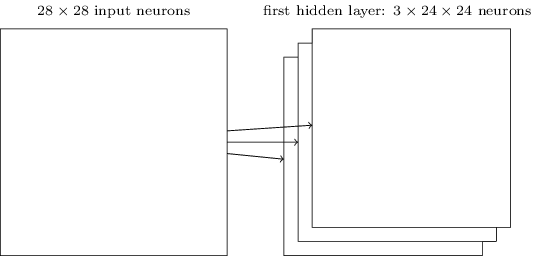
输入层784个神经元，这里我们还原图片原来的样子(28*28)，如下图

盗图2

第一个隐藏层的神经元只与局部区域输入层的神经元相连。下图就是第一个隐藏层的某个神经元与局部区域输入层的神经元相连的情况。

盗图3

这里的局部区域就是局部感受野，它像一个架在输入层上的窗口。其中某一个隐藏层的神经元学习分析了它”视野范围“(局部感受野)里的特征。图中一个隐藏层的神经元有5*5个权值参数与之对应。

我们移动这样一个窗口使它能够扫描整张图，每次移动它都会有一个不同的节点与之对应。我们从输入层左上角开始，如下

盗图4

然后，我们一个像素往右滑动一个像素，如下

盗图5

以此类推可以形成第一个隐藏层，注意我们的图片是2828的，窗口是5 * 5的，可以得到一个2424(24=28-5+1)个神经元的隐藏层

这里我们的窗口指滑动了一个像素，通常说成一步(stride)，也可以滑动多步，这里的stride也是一个超参，训练是可以根据效果调整，同样，窗口大小也是一个超参。

权值共享(Shared weights and biases)
上一节中提到一个隐藏层的神经元有5 * 5个权值参数与之对应。这里要补充下，这24*24个隐藏层的神经元它们的权值和偏移值是共享的 用公式描述下

σ代表的是激活函数，如sigmoid函数等，b就是偏移值，w就是5 * 5个共享权值矩阵，我们用矩阵a表示输入层的神经元，ax,y表示第x+1行第y+1列那个神经元(注意，这里的下标默认都是从0开始计的，a0,0表示第一行第一列那个神经元）所以通过矩阵w线性mapping后再加上偏移值就得到公式中括号里的式子，表示的是隐藏层中第j+1行k+1列那个神经元的输入。参照上面的图，图4就是j=k=0的情况，图5是j=0，k=1. 加上激活函数表示该隐藏神经元的输出。

简化公式：

a1表示隐藏层的输出，a0表示隐藏层的输入，而∗表示卷积操作(convolution operation) 这正是卷积神经网络名字的由来。

由于权值共享，窗口移来移去还是同一个窗口，也就意味着第一个隐藏层所有的神经元从输入层探测(detect)到的是同一种特征(feature)，只是从输入层的不同位置探测到(图片的中间，左上角，右下角等等)，必须强调下，一个窗口只能学到一种特征！另外，窗口还有其他叫法：卷积核(kernal),过滤器(filter)。我们在做图像识别时，光学习一个特征肯定是不够的，我们想要学习更多的特征，就需要更多的窗口。用三个窗口如下图

盗图6

窗口与窗口间的w和b是不共享的，三个窗口就表示有三个w矩阵和三个偏移值b，结果是从整张图片的各个位置学到三种不同的特征。到这里肯定有人会问，你说学到特征了，怎么证明学到了呀？现在我们用20个窗口来学习MNIST里的图片特征，我们只看20个窗口里的权值矩阵w，如果把这20个w画成20张黑白图，每张图片都是5*5(一个权值代表一个像素点)，如下图所示

盗图7

盯着其中的一张看，白色区域表示权值比较小，说明窗口的这部分对输入层的神经元不敏感(responds less)，相反黑色部分表示权值比较大，说明窗口的这部分对输入层的神经元敏感(responds more).每张图片都有明显的黑白区域，这也能够说明CNN确实学到一些和空间结构相关的特征。究竟学的是什么特征呢？这个很难回答清楚，此处暂不深究，更好理解的话可以参考 Visualizing and Understanding Convolutional Networks

权值共享还有一个很大的好处，就是可以大大减少模型参数的个数。我们的例子中，一个窗口参数个数是26(5 * 5+1),20个窗口就是520个参数。CNN可以依靠更少的参数来获得和DNN相同的效果，更少的参数就意味着更快的训练速度，这可是谁都想要的。

池化(Pooling)

CNN还有一个重要思想就是池化，池化层通常接在卷积层后面。引入它的目的就是为了简化卷积层的输出。池化层也在卷积层上架了一个窗口，但这个窗口比卷积层的窗口简单许多，不需要w，b这些参数，它只是对窗口范围内的神经元做简单的操作，如求和，求最大值，把求得的值作为池化层神经元的输入值，如下图，这是一个2*2的窗口

盗图8

值得注意的是，我们此时的窗口每次移动两步，采用的是求最大值的方法，所有称之为max-pooling，刚刚卷积层含有24 * 24个神经元，经过池化后到池化层就是12*12个神经元。通常卷积层的窗口是多个的，池化层的窗口也是多个的。简单来说，卷积层用一个窗口去对输入层做卷积操作，池化层也用一个窗口去对卷积层做池化操作。但是注意这两个操作的本质区别。下面来看一个用三个卷积窗口和跟随其后的池化窗口长啥样。

盗图9

怎么理解max-pooling呢？由于经过了卷积操作，模型从输入层学到的特征反映在卷积层上，max-pooling做的事就是去检测这个特征是否在窗口覆盖范围的区域内。这也导致了，它会丢失这种特征所在的精准位置信息，所幸的是池化层可以保留相对位置信息。而后者相比而言比前者更重要。池化层一个最大的好处：经过池化后，大大减少了我们学到的特征值，也就大大减少了后面网络层的参数

(上图可以看出池化层的神经元数明显少于卷积层神经元数)。

max-pooling技术只是池化技术的一种，还有一种比较常用的是L2-pooling,与max-pooling唯一的区别就是在池化窗口扫过的区域里做的操作不是求最大值，而是所有神经元平方后求和再开根号，这和我们L2正则对权值参数的操作是一样的。实际操作中，这两种方式都是比较常用的。池化操作方式的选择也是我们调参工作的一部分，我们可以根据validation data集来调节，选择更好的池化操作。

总的来看

介绍完CNN的三个几本思想概念后我们把它串起来看下。

盗图10
从左往右依次是输入层，卷积层，池化层，输出层。输入层到卷积层，池化层到输出层是全连接，这和DNN是一样的。
CNN的网络架构，是一层一层组合起来的，层与层之间的行为也是有对应的权值w和偏移值b决定的，并且它们的目的也是一致的:通过training data来学习网络结构中的w和b，从而能把输入的图片正确分类。

数学原理：CNN的BP算法

首先看看卷积层，卷积层正向传播的公式：

的关系变了： 这里和DNN的区别就是卷积操作，对于含有卷积的式子求导，卷积核(W)被旋转180度，意思就是上下翻转，然后左右翻转，因此我们的公式(12)变成了: 对卷积求导原理感兴趣的同学可以自行百度。 有了对卷积求导的知识就可以很轻易写出： ,因为b是一个向量，而这里的因为经过了卷积求导后变成了一个三维的张量，所以可以近似地用一个误差向量代替：

到这里我们已经解决了如何求卷积层上的。

在基本思想里面讲到，前向传播时池化层一般的操作是MAX或Average等，我们现在是要从压缩过的误差第k个子矩阵是:

假设我们池化窗口大小是2*2,则将其还原成原来大小就是：

这里假设我们之前前向传播时记录的最大值的位置分别是左上，右下，右上，左下，unsample后就是： 的偏导，公式如下：

概括下:

这里不同的池化操作也对应着不同的unsample操作。