数据结构之栈 - 前缀表达式、中缀表达式、后缀表达式
中缀表达式
我们经常看到的表达式,入 (2+3)*2+4这样的表达式,就称为中缀表达式。中缀表达式,对读者来说,很好理解。但是计算机运算时候,需要判断括号和各种运算符的优先级,就比较难以处理。
中缀表达式可以转换成一颗表达式树,将中缀表达式转化为表达式树方法:表达式树的树叶是操作数,而其他的节点为操作符,根节点为优先级最低且靠右的操作符(如上述表达式优先级最低的是+,所以根为+),圆括号不包括
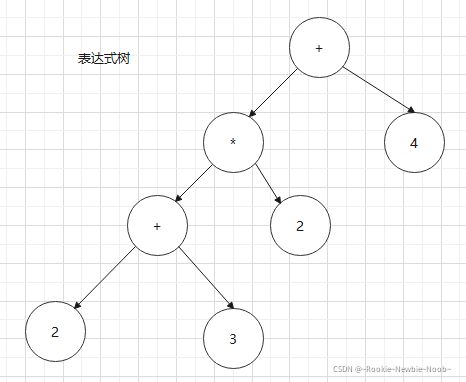
前缀表达式
前缀表达式又称为波兰式,前缀表达式的运算位于操作数之前。
对表达式树做前序遍历,便得到了前缀表达式(波兰式)。如 (2+3)*2+4的前缀表达式为+ * + 2 3 2 4
后缀表达式
后缀表达式又称为逆波兰式,对表达式树做后续遍历,便得到了后缀表示。如(2+3)*2+4的后缀表达式为2 3 + 2 * 4 +
后缀表达式计算器
public class PolandNotation {
public static void main(String[] args) {
// String suffixExpression = "3 4 + 5 * 6 -";
String suffixExpression = "2 3 + 2 * 4 +";
List<String> list = getListByString(suffixExpression);
int res = calculate(list);
System.out.printf("计算结果:%d\n", res);
}
private static int calculate(List<String> list) {
Stack<String> stack = new Stack<>();
for (int i = 0; i < list.size(); ++i) {
String s = list.get(i);
if (s.matches("\\d+")) {
stack.push(s);
continue;
}
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res = 0;
switch (s) {
case "+":
res = num1 + num2;
break;
case "-":
res = num1 - num2;
break;
case "*":
res = num1 * num2;
break;
case "/":
res = num1 / num2;
break;
default:
throw new RuntimeException("表达式有错误");
}
stack.push(""+res);
}
return Integer.parseInt(stack.pop());
}
private static List<String> getListByString(String suffixExpression) {
String[] s = suffixExpression.split(" ");
List<String> list = Arrays.asList(s);
return list;
}
}
中缀表达式转后缀表达式
详细步骤
- 初始化两个栈:运算符栈 s1 和存储中间结果的栈 s2。
- 从左到右扫描中缀表达式。
- 遇到操作数时,将其压入栈 s2。
- 遇到运算符时,比较其与 s1 栈顶运算符的优先级:
- 如果s1为空,或者栈顶运算符号为左括号"(",则直接将此运算符入栈。
- 否则,若优先级比栈顶的高,也将运算符压入s1。
- 否则,将s1栈顶的运算符弹出并压入s2中,再次转到(4.1)与s1中的新的栈顶运算符比较。
- 遇到括号时:
- 如果是左括号“(”,则直接压入s1。
- 如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号“(“为止,此时将这一对括号丢弃。
- 重复步骤2~5,直到表达式的最右边。
- 将s1中剩余的运算符依次弹出并压入s2。
- 依次弹出s2中的元素并输出,结果的逆序即为
中缀表达式对应的后缀表达式。
代码实现
import java.util.*;
/**
* 中缀表达式转后缀表达式
*/
public class MiddleToSuffixNotation {
public static void main(String[] args) {
// String middleExpression = "1+((2+3)*4)-5";
String middleExpression = "1+2*((32+2)-5)+4";
List<String> middleList = StringToList(middleExpression);
List<String> suffixList = middleToSuffix(middleList);
System.out.printf("%s=", middleExpression);
for(int i = 0; i < suffixList.size(); ++i) {
if (i!=0){
System.out.printf(" ");
}
System.out.printf(suffixList.get(i));
}
System.out.println();
int res = calculate(suffixList);
System.out.printf("计算结果:%d\n", res);
}
private static int calculate(List<String> list) {
Stack<String> stack = new Stack<>();
for (int i = 0; i < list.size(); ++i) {
String s = list.get(i);
if (s.matches("\\d+")) {
stack.push(s);
continue;
}
int num2 = Integer.parseInt(stack.pop());
int num1 = Integer.parseInt(stack.pop());
int res = 0;
switch (s) {
case "+":
res = num1 + num2;
break;
case "-":
res = num1 - num2;
break;
case "*":
res = num1 * num2;
break;
case "/":
res = num1 / num2;
break;
default:
throw new RuntimeException("表达式有错误");
}
stack.push(""+res);
}
return Integer.parseInt(stack.pop());
}
private static List<String> middleToSuffix(List<String> middleList) {
Stack<String> stack1 = new Stack<>();
Stack<String> stack2 = new Stack<>();
for (int i = 0; i < middleList.size(); ++i) {
String s = middleList.get(i);
if (s.matches("\\d+")) {
stack2.push(s);
continue;
}
// 如果遇到的是操作符
if (isOperation(s.charAt(0))) {
while (true) {
if (stack1.isEmpty()) {
stack1.push(s);
break;
}
String top = stack1.peek();
if ("(".equals(top)) {
stack1.push(s);
break;
}
// 若当前运算符 优先级高于栈顶元素
if (priority(s.charAt(0)) > priority(top.charAt(0))) {
stack1.push(s);
break;
}
top = stack1.pop();
stack2.push(top);
}
}
// 如果遇到左括号
if ("(".equals(s)) {
stack1.push(s);
}
// 如果遇到右括号
if (")".equals(s)) {
while (!stack1.isEmpty()) {
String pop = stack1.pop();
if("(".equals(pop)) {
break;
}
stack2.push(pop);
}
}
}
while (!stack1.isEmpty()) {
String s = stack1.pop();
stack2.push(s);
}
List<String> list = new ArrayList<>();
while (!stack2.isEmpty()) {
list.add(stack2.pop());
}
Collections.reverse(list);
return list;
}
private static List<String> StringToList(String middleExpression) {
List<String> list = new ArrayList<>();
String num = "";
for (int i = 0; i < middleExpression.length(); ++i) {
char s = middleExpression.charAt(i);
if (s >='0' && s <= '9') {
num += s;
} else {
if (!"".equals(num)) {
list.add(num);
}
list.add(""+s);
num = "";
}
}
if (!"".equals(num)) {
list.add(num);
}
return list;
}
public static boolean isOperation(char ch) {
return ch == '+' || ch == '-' || ch == '*' || ch == '/';
}
public static int priority(char ch) {
if (ch == '*' || ch == '/') {
return 1;
} else if (ch == '-' || ch == '+') {
return 0;
} else {
throw new RuntimeException("运算符有错误,程序退出");
}
}
}