二叉树（C++ 伪代码）

目录

二叉树的种类 

 二叉树的定义

 二叉树的遍历

助记小技巧：

二叉树遍历种类：

前序遍历

遍历顺序：根左右，先遍历根节点，再依次遍历左右孩子

LeetCode 144 二叉树的前序遍历 

LeetCode 257 二叉树的所有路径 

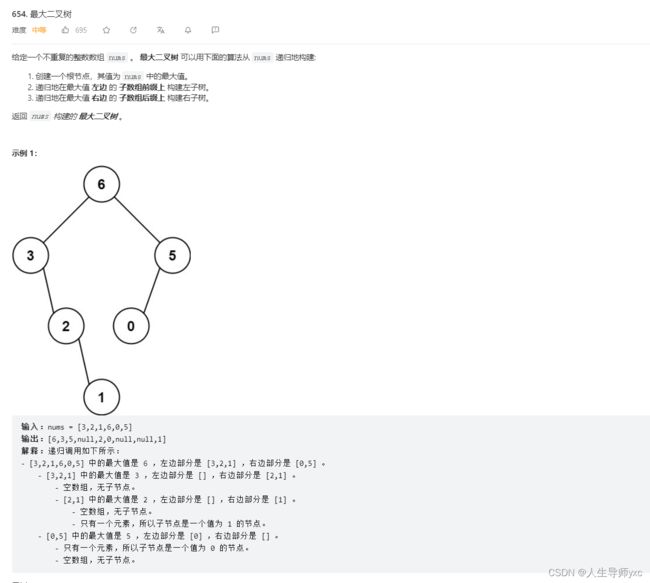
LeetCode 654 最大二叉树 

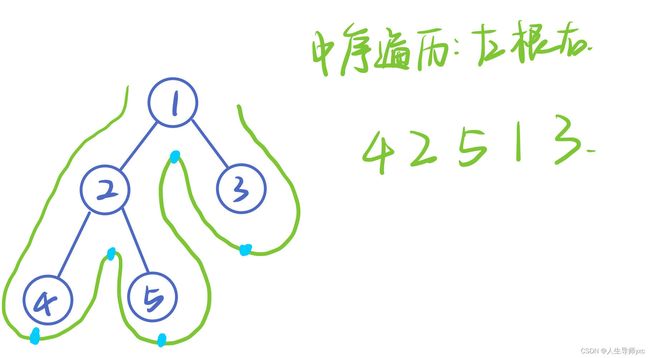
中序遍历

遍历顺序：先遍历左孩子，再遍历根节点，最后遍历右孩子

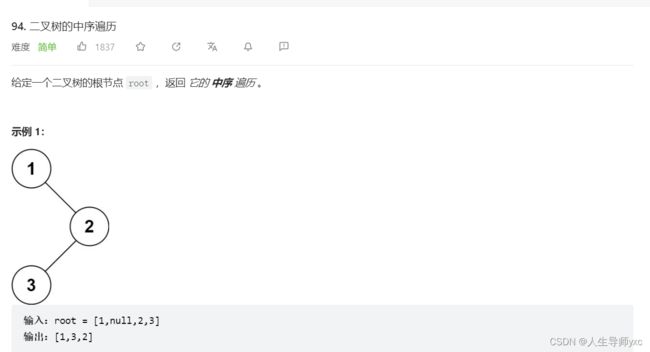
LeetCode 94 二叉树的中序遍历

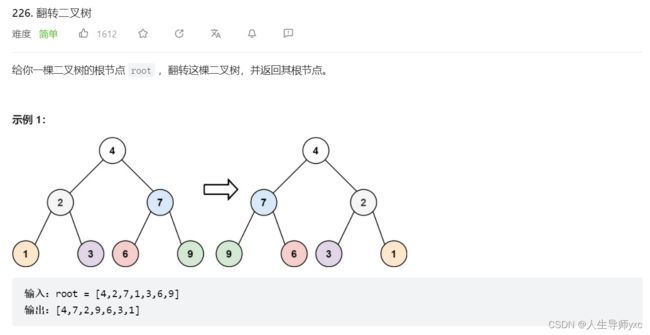
LeetCode 226 翻转二叉树

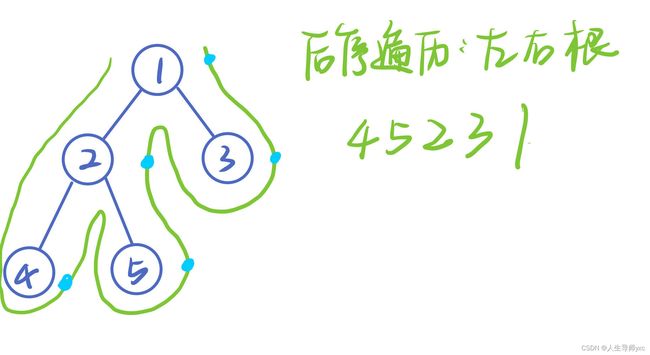
后序遍历

遍历顺序：先依次遍历左右孩子， 再遍历根节点

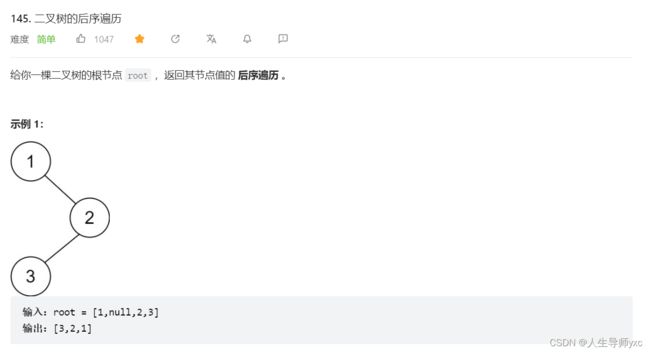
 LeetCode 145 二叉树的后序遍历

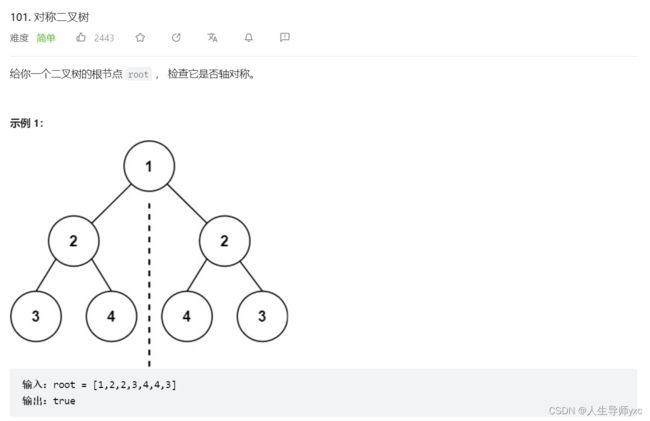
LeetCode 101 对称二叉树 

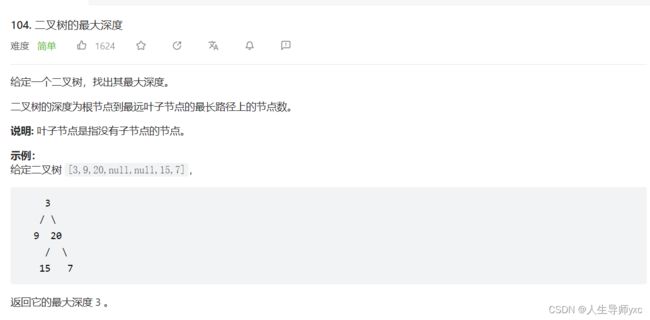
LeetCode 104 二叉树的最大深度

 LeetCode 111 二叉树的最小深度​编辑

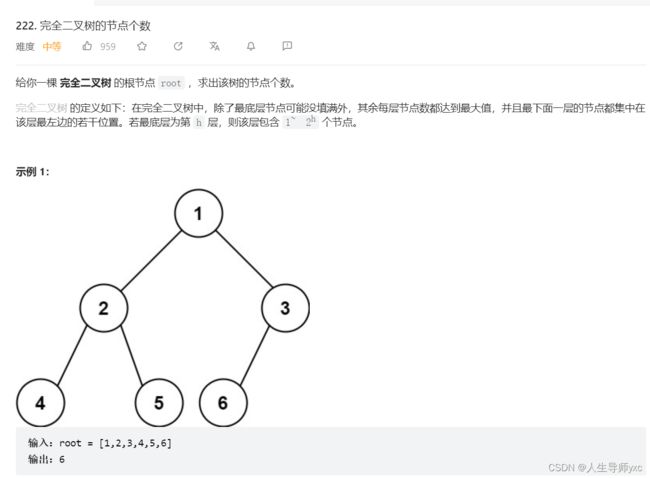
LeetCode 222 完全二叉树的节点个数 

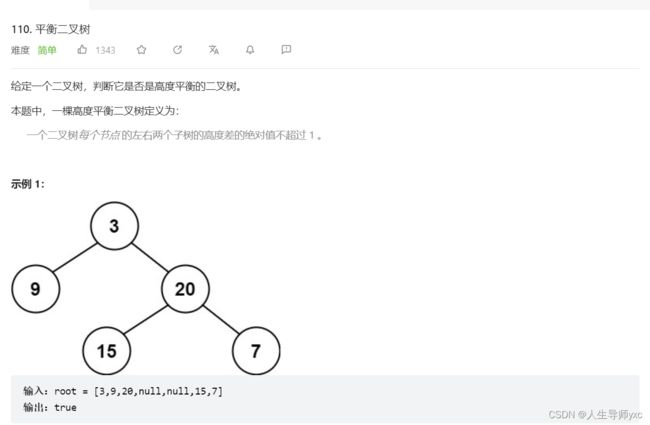
LeetCode 110 平衡二叉树 

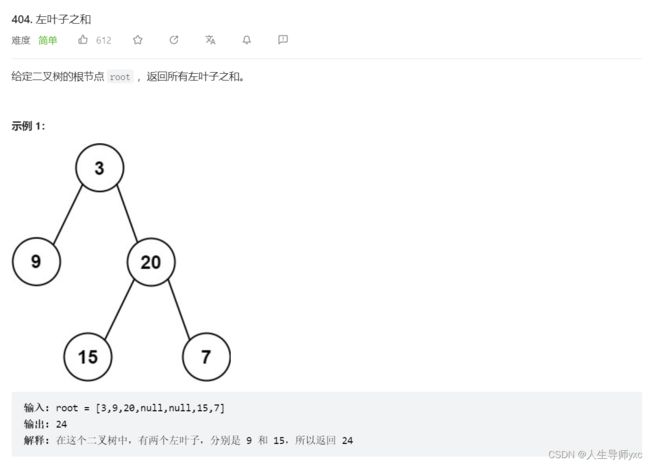
 LeetCode 404 左叶子之和

 LeetCode 112 路径总和​编辑

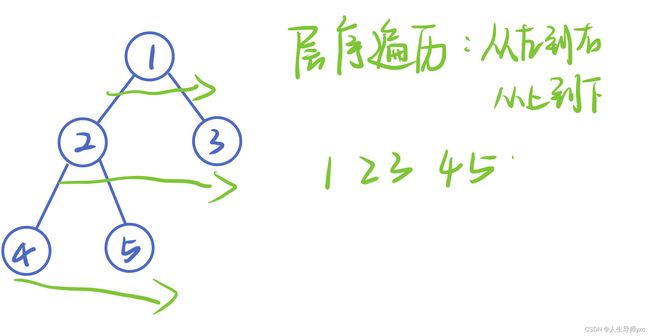
层序遍历

底层实现：队列

遍历顺序（bfs）：从上到下，从左到右

LeetCode 102 二叉树的层序遍历 

LeetCode 107 二叉树的层序遍历II 

LeetCode 199 二叉树的右视图

LeetCode 513 找树左下角的值 

特殊的树形结构

完美二叉树（满二叉树）

定义：

完全二叉树

定义:

二叉搜索树

定义：

LeetCode 700 二叉搜索树中的搜索 

其它：

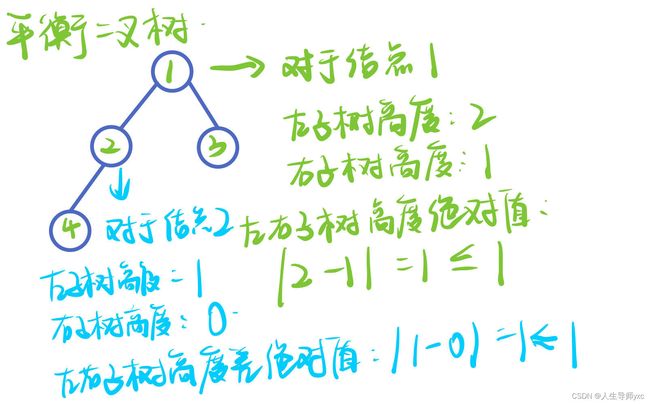
平衡二叉树 

定义：

二叉树的创建

注意：

中序+后序：

明确遍历顺序：

整体思路：

具体实现过程：

样例模拟：

LeetCode 106 从中序与后序遍历序列构造二叉树 ​​​​​​​

中序+前序：

明确遍历顺序：

整体思路：

具体实现过程：

样例模拟：

---

二叉树的种类 

 二叉树的定义

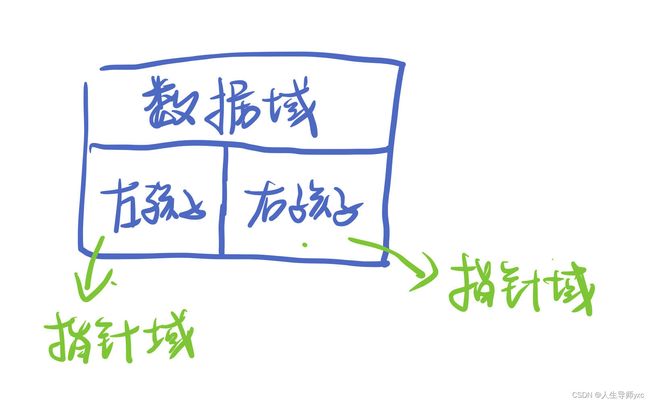
//二叉树的定义
/*C语言*/
struct TreeNode
{
    int val;//数据域
    struct TreeNode* left;//指针域->指向左孩子
    struct TreeNode* right;//指针域->指向右孩子
}
/*C++*/
struct TreeNode 
{
       int val;
       TreeNode *left;
       TreeNode *right;
       TreeNode() : val(0), left(nullptr), right(nullptr) {}
       TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
       TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

 二叉树的遍历

助记小技巧：

根据根节点的位置来判断是什么遍历顺序

根节点在前面 就是前序遍历

根节点在中间 就是中序遍历

根节点在后面 就是后序遍历

二叉树遍历种类：

深度优先遍历（dfs）-> 底层通过栈来实现:

前、中、后序遍历

宽度优先遍历（bfs）->底层通过队列来实现：

层序遍历

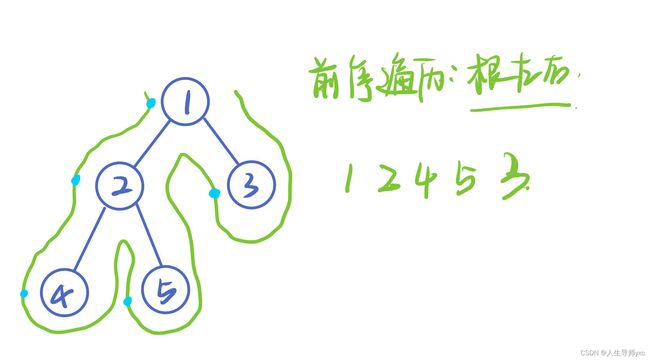
前序遍历

遍历顺序：根左右，先遍历根节点，再依次遍历左右孩子

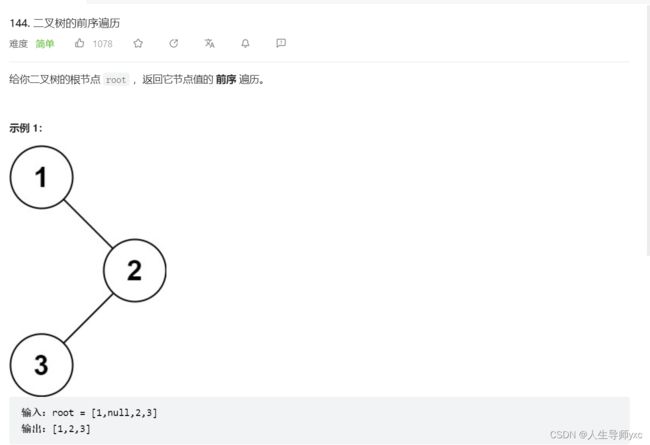
LeetCode 144 二叉树的前序遍历 

代码1（C++ 迭代法）：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector preorderTraversal(TreeNode* root) {
        vector res;
        stack st;
        TreeNode* cur = root;
        st.push(cur);
        while (st.size())
        {
            cur = st.top();
            st.pop();
            if(cur != NULL)
            {
                res.push_back(cur->val);
                st.push(cur->right);
                st.push(cur->left);
            }
            
        }
        return res;

    }
};

代码2 （C语言 递归法） ：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
void order(struct TreeNode* root, int* res, int* resSize)
{
    if (root == NULL) return;
    res[(*resSize) ++] = root->val;
    order(root->left, res, resSize);
    order(root->right, res, resSize);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    int* res = malloc(sizeof(int) * 501);//存储返回结果
    *returnSize = 0;//初始化
    order(root, res, returnSize);
    return res;
}

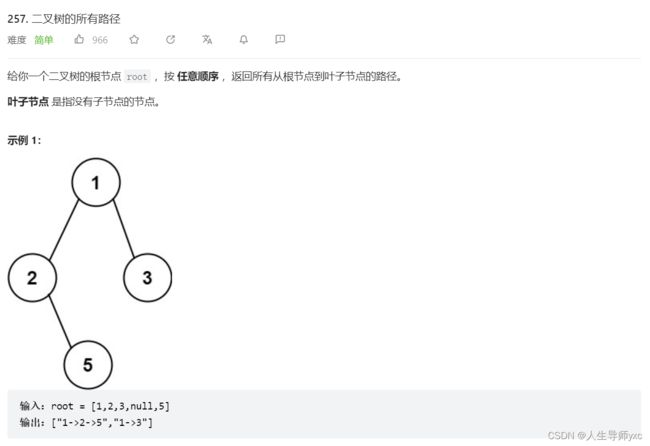
LeetCode 257 二叉树的所有路径 

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void traversal(TreeNode* node, vector &path, vector &res)
    {
        
        path.push_back(node->val);
        if (node->left == NULL && node->right == NULL)
        {
            string tmp;
            tmp.clear();
            int len = path.size();
            int t = 1;
            for (int i = 0; i < len; i ++ )
            {
                if (t == 1) t = 0;
                else tmp += "->";
                if (path[i] < 0) tmp += '-';
                int sum = abs(path[i]);
                char num[110];
                int cnt = 0;
                while (sum)
                {
                    int m = sum % 10;
                    num[cnt ++] = m + '0';
                    sum /= 10;
                }
                for (int i = cnt - 1; i >= 0; i -- )
                {
                    tmp += num[i];
                }
                
            }
            res.push_back(tmp);
            return;
        }
        if (node->left != NULL)
        {
            traversal(node->left, path, res);
            path.pop_back();
        }
        if (node->right != NULL)
        {
            traversal(node->right, path, res);
            path.pop_back();
        }
    }
    vector binaryTreePaths(TreeNode* root) {
        //存储返回结果
        vector res;
        vector path;
        traversal(root, path, res);
        return res;
        
    }
};

LeetCode 654 最大二叉树 

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* traversal(vector& nums, int leftindex, int rightindex)
    {
        if (leftindex >= rightindex) return NULL;
        //用前序 中左右
        //中
        int maxval = nums[leftindex];
        int index = leftindex;//记录最大值的下标
        for (int i = leftindex + 1; i < rightindex; i ++ )
        {
            if (nums[i] > maxval)
            {
                maxval = nums[i];
                index = i;
            }
        }
        TreeNode* node = new TreeNode(maxval);
        //左
            node->left = traversal(nums, leftindex, index);
        //右
            node->right = traversal(nums, index + 1, rightindex);
        return node;
    }
    TreeNode* constructMaximumBinaryTree(vector& nums) {
    return traversal(nums, 0, nums.size());
    }
};

中序遍历

遍历顺序：先遍历左孩子，再遍历根节点，最后遍历右孩子

LeetCode 94 二叉树的中序遍历

代码1（C++ 迭代法）：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector inorderTraversal(TreeNode* root) {
        vector res;
        stack st;
        TreeNode* cur = root;
        while (cur != NULL || st.size())
        {
            if (cur != NULL)
            {
                st.push(cur);    
                cur = cur->left;
            }
            else
            {
                cur = st.top();
                st.pop();
                res.push_back(cur->val);
                cur = cur->right;
            }
        }
        return res;
    
    }
};

代码2（C语言 递归法）：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
void order(struct TreeNode* root, int* res, int *resSize) 
{
    if (root == NULL) return;
    order(root->left, res, resSize);
    res[(*resSize)++] = root->val;
    order(root->right, res, resSize);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){

    int* res = malloc(sizeof(int) * 501);
    *returnSize = 0;
    order(root, res, returnSize);
    return res;
}

LeetCode 226 翻转二叉树

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
    if (root == NULL) return root;
    
    invertTree(root->left);
    swap(root->left, root->right);
    invertTree(root->left);

    return root;
    }
};

后序遍历

遍历顺序：先依次遍历左右孩子， 再遍历根节点

 LeetCode 145 二叉树的后序遍历

 代码1（C ++ 迭代法）：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector postorderTraversal(TreeNode* root) {
    vector res;//存储返回结果
    stack st;
    TreeNode* cur = root;
    st.push(cur);
    while (st.size())
    {
        cur = st.top();
        st.pop();
        if (cur != NULL)
        {
            res.push_back(cur->val);
            st.push(cur->left);
            st.push(cur->right);
        }
    }
        reverse(res.begin(), res.end());
        return res;
    }
};

 代码2（C语言 递归法）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
//左右中
void order(struct TreeNode* root, int* res, int* resSize)
{
    if (root == NULL) return;
    order(root->left, res, resSize);
    order(root->right, res, resSize);
    res[(*resSize) ++] = root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
    int* res = malloc(sizeof(int) * 501);//存储返回结果
    *returnSize = 0;//初始化
    order(root, res, returnSize);
    return res;
}

LeetCode 101 对称二叉树 

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool Check(TreeNode* left, TreeNode* right)
    {
    //左 右
    //空 空 true
    //空 不空 false
    //不空 空 flase
    //值不同 false
    //值相同 下一层递归
    if (left == NULL && right == NULL) return true;
    else if (left == NULL && right != NULL) return false;
    else if (left != NULL && right == NULL) return false;
    else if (left->val != right->val) return false;
    bool outside = Check(left->left, right->right);
    bool inside = Check(left->right, right->left);
    bool flag = outside && inside;
    return flag;
    }
    bool isSymmetric(TreeNode* root) {
    bool lflag = Check(root, root);
    return lflag;
    }
};

LeetCode 104 二叉树的最大深度

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
    if (root == NULL) return 0;
    int left_height = maxDepth(root->left);
    int right_height = maxDepth(root->right);
    int height = 1 + max(left_height, right_height);
    return height;
    }
};

 LeetCode 111 二叉树的最小深度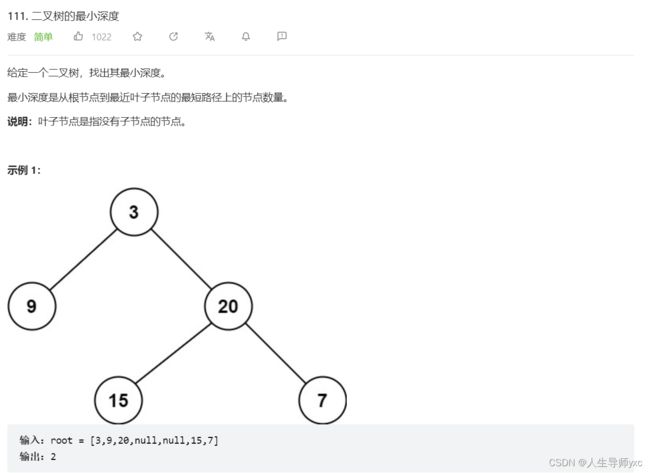

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
    //递归终止条件
    if (root == NULL) return 0;
    //后序遍历 左右中 
    int left_height = minDepth(root->left);
    int right_height = minDepth(root->right);
    //左 右
    //空 不空
    //不空 空
    //不空 不空
    if (root->left == NULL && root->right != NULL)
        return 1 + right_height;
    if (root->left != NULL && root->right == NULL)
        return 1 + left_height;
    int height = 1 + min(left_height, right_height);
    return height;
        
    }
};

LeetCode 222 完全二叉树的节点个数 

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        if (root == NULL) return 0;
        TreeNode* Left = root->left, *Right = root->right;
        int lefth = 0, righth = 0;
        while (Left)
        {
            Left = Left->left;
            lefth ++;
        }
        while (Right)
        {
            Right = Right->right;
            righth ++;
        }
        //判断是不是完全二叉树
        if (lefth == righth) return (2 << lefth) - 1;
        
        int l = countNodes(root->left);
        int r = countNodes(root->right);
        int res = l + r + 1;
        return res;
    }
};

LeetCode 110 平衡二叉树 

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int GetHeight(TreeNode* Node)
    {
        if (Node == NULL) return 0;
        int leftheight = GetHeight(Node->left);
        if (leftheight == -1) return -1;
        int rightheight = GetHeight(Node->right);
        if (rightheight == -1) return -1;
        int res = 0;
        if (abs(leftheight - rightheight) > 1) res = -1;
        else
        {
            res = 1 + max(leftheight, rightheight);
        }
        return res;
    }
    bool isBalanced(TreeNode* root) {
        int t = GetHeight(root);
        if (t == -1) return false;
        else return true;

    }
};

 LeetCode 404 左叶子之和

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
    if (root == NULL) return 0;
    if (root->left == NULL && root->right == NULL) return 0;
    //后序 左右中
    //左
    int sumleftleaves = sumOfLeftLeaves(root->left);
    if (root->left != NULL && root->left->left == NULL && root->left->right == NULL)
        sumleftleaves = root->left->val;
    //右
    int sumrightleaves = sumOfLeftLeaves(root->right);
    //中    
    int sum  = sumleftleaves + sumrightleaves;
    return sum;
    }
}; 

 LeetCode 112 路径总和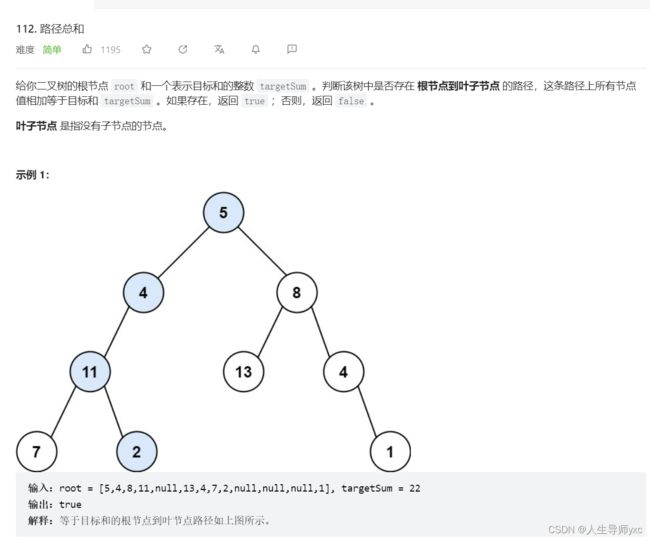

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool traversal(TreeNode* root, int targetSum)
    {
    if (root->left == NULL && root->right == NULL && targetSum == 0) return true;
    if (root->left == NULL && root->right == NULL) return false;
    if (root->left)
    {
        targetSum -= root->left->val;
        if (traversal(root->left, targetSum)) return  true;
        targetSum += root->left->val;
    }
    if (root->right)
    {
        targetSum -= root->right->val;
        if (traversal(root->right, targetSum)) return true;
        targetSum += root->right->val;
    }
        return false;   
    }
    bool hasPathSum(TreeNode* root, int targetSum) {
    if (root == NULL) return false;
    return traversal(root, targetSum - root->val);
    }
};

层序遍历

底层实现：队列

遍历顺序（bfs）：从上到下，从左到右

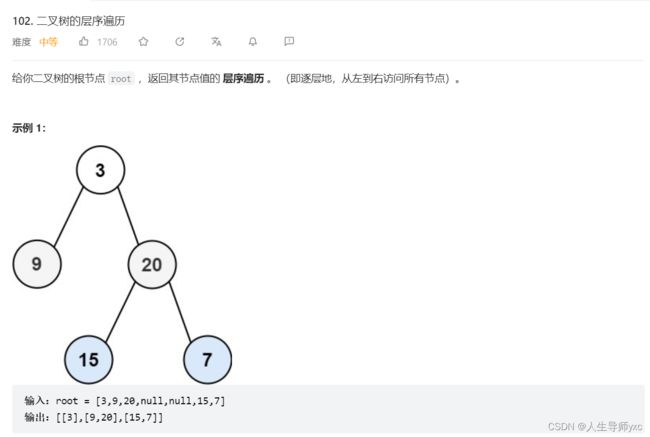
LeetCode 102 二叉树的层序遍历 

代码（C++ 队列 迭代法）：

class Solution {
public:
    vector> levelOrder(TreeNode* root) {
        vector> res;//存储返回结果
        queue qu;
        TreeNode* cur = root;
        if (cur != NULL) qu.push(cur);
        
        while (qu.size())
        {
            int size = qu.size();
            vector ans;
            while (size --)
            {
                cur = qu.front();
                qu.pop();
                ans.push_back(cur->val);
                if (cur->left != NULL) qu.push(cur->left);
                if (cur->right != NULL) qu.push(cur->right);
            }
            res.push_back(ans);
        }
        return res;
    }
};

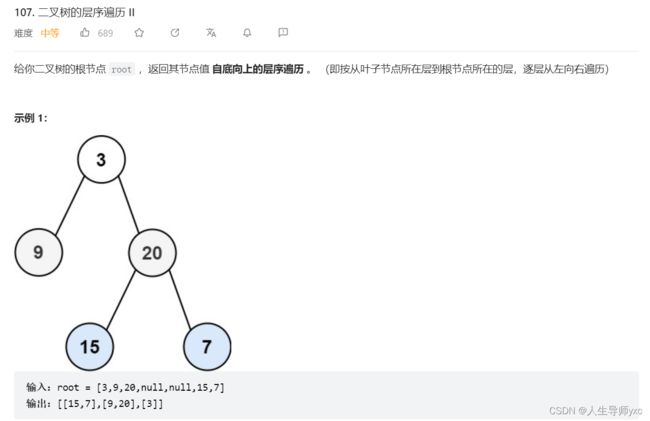
LeetCode 107 二叉树的层序遍历II 

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector> levelOrderBottom(TreeNode* root) {
        vector> res;//存储返回结果
        queue qu;
        TreeNode* cur = root;
        if (cur != NULL) qu.push(cur);
        
        while (qu.size())
        {
            int size = qu.size();
            vector ans;
            while (size --)
            {
                cur = qu.front();
                qu.pop();
                ans.push_back(cur->val);
                if (cur->left != NULL) qu.push(cur->left);
                if (cur->right != NULL) qu.push(cur->right);
            }
            res.push_back(ans);
        }
        reverse(res.begin(), res.end());
        return res;

    }
};

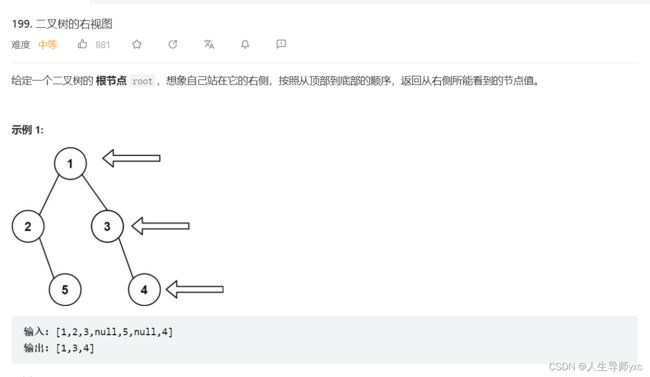
LeetCode 199 二叉树的右视图

代码： 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector rightSideView(TreeNode* root) {
        vector res;//存储返回结果
        queue qu;
        TreeNode* cur = root;
        if (cur != NULL) qu.push(cur);
        
        while (qu.size())
        {
            int size = qu.size();
            for (int i = 0; i < size; i ++)
            {
                cur = qu.front();
                qu.pop();
                if (i == (size - 1)) res.push_back(cur->val);
                if (cur->left != NULL) qu.push(cur->left);
                if (cur->right != NULL) qu.push(cur->right);
            }
        }
        return res;
    }
};

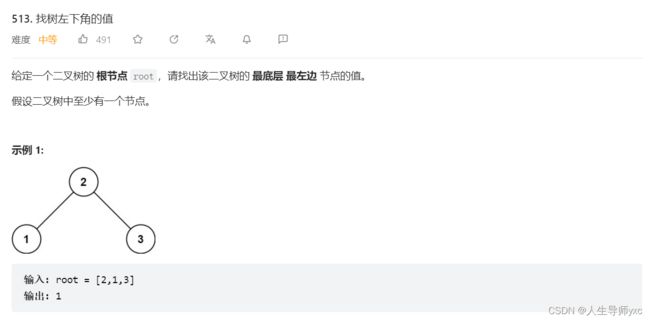
LeetCode 513 找树左下角的值 

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
    queue que;
    TreeNode* cur = root;
    if (cur != NULL)
        que.push(cur);
        
    int result = 0;
    while (que.size())
    {
        int size = que.size();
        for(int i = 0; i <  size; i ++ )
        {
            cur =  que.front();
            que.pop();
            if(i == 0) result = cur->val;
            if (cur->left) que.push(cur->left);
            if (cur->right) que.push(cur->right);
        }
    }
        return result;
    }
};

特殊的树形结构

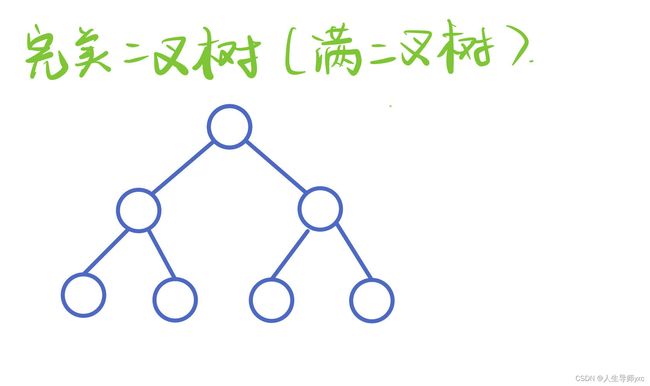
完美二叉树（满二叉树）

定义：

显然，一个完美二叉树必然是一个完全二叉树 

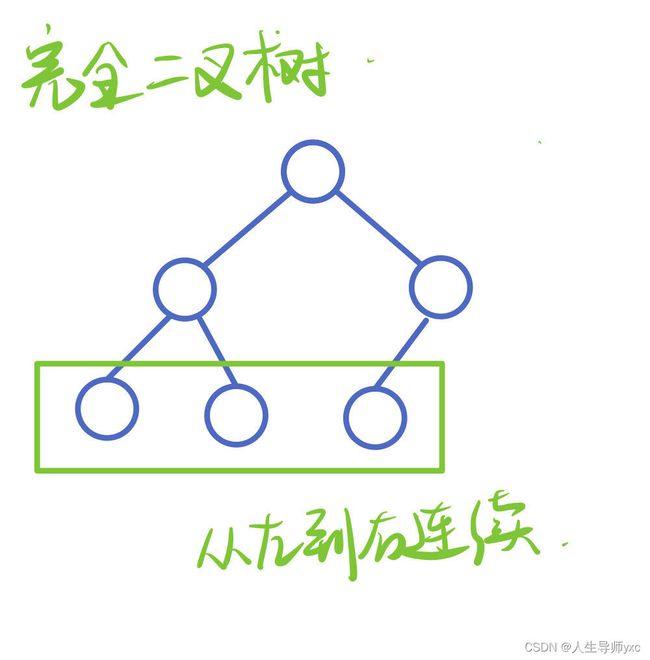
完全二叉树

定义:

叶子节点从左到右连续

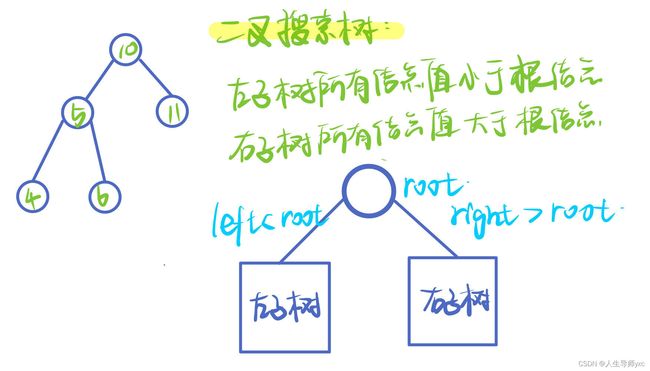
二叉搜索树

定义：

左小右大

左子树所有节点值小于根节点

右子树所有节点值大于根节点

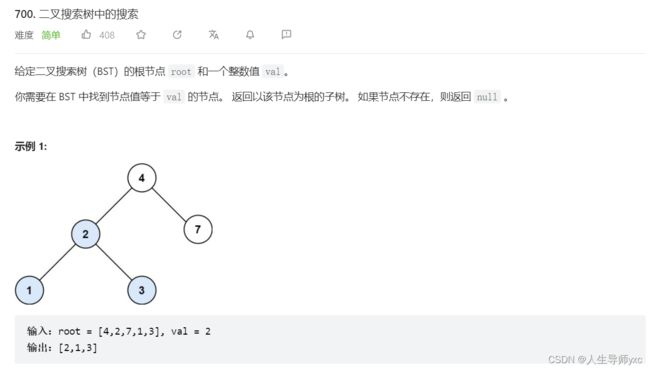
LeetCode 700 二叉搜索树中的搜索 

 代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
    while (root)
    {
        if (root->val > val) root = root->left;
        else if (root->val < val) root = root->right;
        else return root;
    }
        return NULL;
    }
};

其它：

题目还有很多

有兴趣可以去刷一刷

都是LeetCode上面的

平衡二叉树 

定义：

任何一个节点左右子树的高度差的绝对值小于等于1

二叉树的创建

注意：

若想要创建一个二叉树，必须给出中序遍历的顺序

即要给出中序+后序，或者中序+前序的遍历结果

中序+后序：

明确遍历顺序：

中序：左根右

后序： 左右根

整体思路：

根据后序遍历结果确定根节点

根据中序遍历结果找左右子树

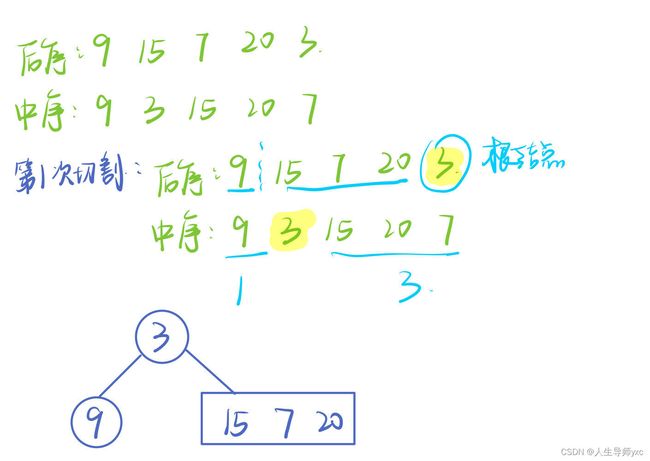
具体实现过程：

1.后序遍历数组的最后一个节点为根节点元素

2.通过后序数组所找到的根节点，在中序遍历数组中找到该根节点，以该点作为切割点

3.切中序数组，该点左边为左子树，该点右边为右子树

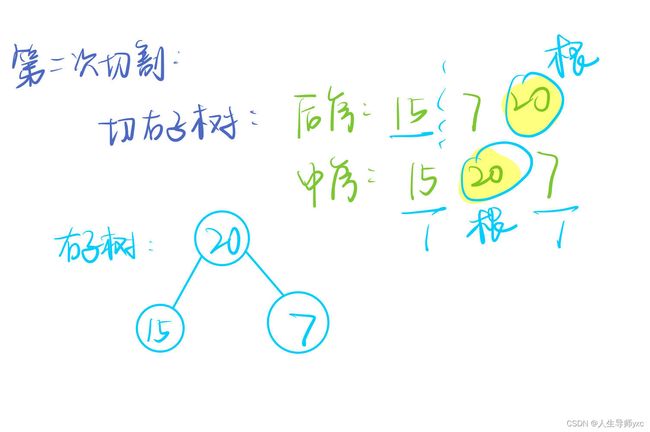
4.切后序数组，通过中序所找到的根节点的位置，根据长度大小可以将后序切成左右子树

5.递归处理左右子树

样例模拟：

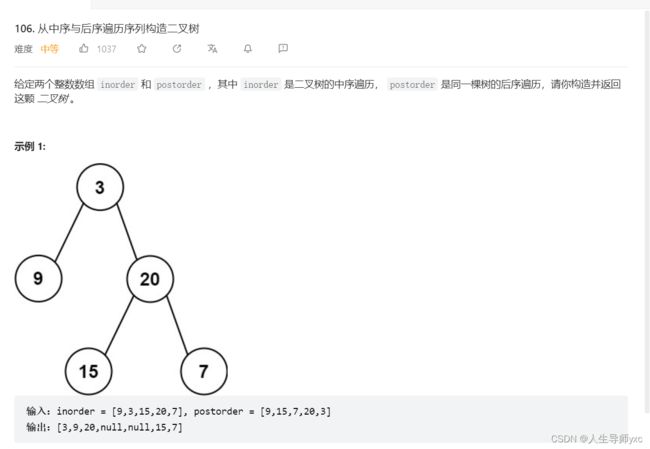
LeetCode 106 从中序与后序遍历序列构造二叉树 

代码： 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* traversal(vector& inorder, vector& postorder)
    {
        if (postorder.size() == 0) return NULL;
        int rootvalue = postorder[postorder.size() - 1];
        TreeNode* root = new TreeNode(rootvalue);
        if (postorder.size() == 1) return root;
        //切中序
        int index;
        for (index = 0; index < inorder.size(); index ++ )
            if (inorder[index] == rootvalue) break;
        vector leftinorder(inorder.begin(), inorder.begin() + index);
        vector rightinorder(inorder.begin() + index + 1, inorder.end());
        //切后序
        postorder.resize(postorder.size() - 1);
        vector leftpostorder(postorder.begin(), postorder.begin() + index);
        vector rightpostorder(postorder.begin() + index, postorder.end());
        
        root->left = traversal(leftinorder, leftpostorder);
        root->right = traversal(rightinorder, rightpostorder);
        
        return root;
    }
    TreeNode* buildTree(vector& inorder, vector& postorder) {
    if (inorder.size() == 0 || postorder.size() == 0) return NULL;
        return traversal(inorder, postorder);
    }
};

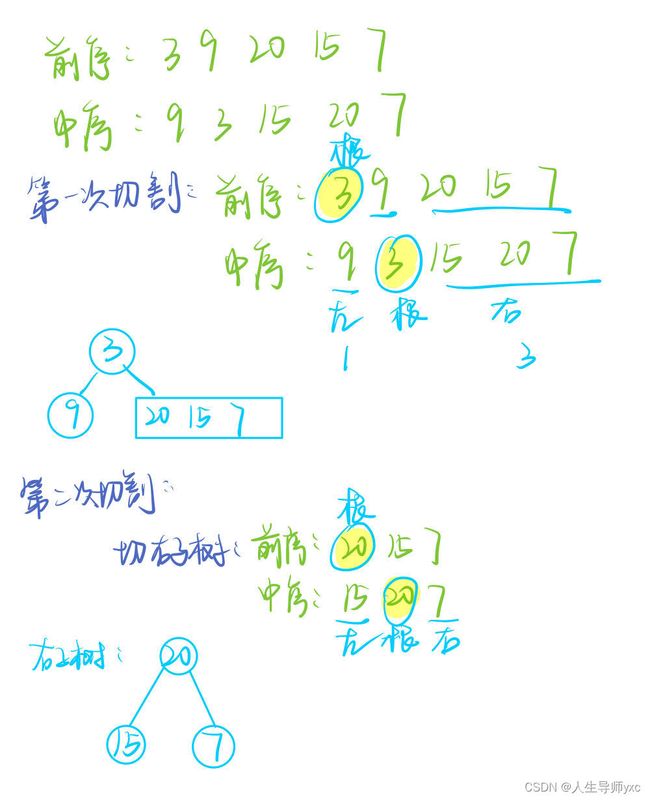
中序+前序：

明确遍历顺序：

中序：左根右

前序： 根左右

整体思路：

根据前序遍历结果确定根节点

根据中序遍历结果找左右子树

具体实现过程：

1.前序遍历数组的第一个节点为根节点元素

2.通过前序数组所找到的根节点，在中序遍历数组中找到该根节点，以该点作为切割点

3.切中序数组，该点左边为左子树，该点右边为右子树

4.切后序数组，通过中序所找到的根节点的位置，根据长度大小可以将后序切成左右子树

5.递归处理左右子树

样例模拟：