武汉理工大学计算机考研复试-算法与程序设计(绿皮书算法java实现)
经典算法设计与分析
递归
函数在运行时调用自身,并且一定要包含条件语句,在合适的时候终止递归
//2013年算一个M的N次方,要求用递归;
public class recursion {
public static void main(String[] args){
System.out.println(f(5,3));
}
public static Integer f(int M,int N){
if(N==1){
return M;
}
else {
return M*f(M,N-1);
}
}
}
// 用递归求f(n)=f(n-1)+f(n-2) n>2;n=1时 f(n)=1;n=2 时 f(n)=1;
public static void main(String[] args) {
System.out.println(f(5));
}
public static int f(int n){
//注意这里n==2与n==1在一个判断式内,因为n>2时f(n-1)+f(n-2)才成立
if(n==1||n==2){
return 1;
}
else {
return f(n-1)+f(n-2);
}
}
迭代法
有一定规律,每次循环都是从上次运算结果中获得数据,本次运算的结果都要为下次运算作准备
//求阶乘!(6的阶乘)
public static void main(String[] args) {
System.out.println(calculate(6));
}
public static int calculate(int n){
int result=1;
for (int i=n;i>=1;i--){
result=result*i;
}
return result;
}
分治法
分治法解决问题大多要利用递归函数,不断递归(
注意递归需要有终止条件)才能得到问题的最小解,然后递归回溯得到原问题的解
归并算法
归并算法的关键点在于并即合并数组的部分,分的操作对array数组无实质上的影响。
该算法要注意的要点在于递归的顺序以及两子序列合并时的初始值
这里借助temp数组来完成子序列合并时的数据转移,并在合并完成后将temp数组赋值给array数组
图解:
public static void main(String[] args) {
int[] array= {
8,4,5,7,1,3,6,2};
int[] temp = new int[array.length];
sort(0,array.length-1,array,temp);
System.out.println(Arrays.toString(array));
}
//划分array
public static void sort(int left,int right,int[] array,int[] temp){
if (left<right){
int mid=(left+right)/2;
//划分左序列
sort(left,mid,array,temp);//左序列为从left到mid
//划分右序列
sort(mid+1,right,array,temp);
//合并上面划分的两端子序列
merge(left,mid,right,array,temp);
}
}
//合并左右两个子序列
public static void merge(int left,int mid,int right,int[] array,int[] temp){
int i=left;//初始化左边序列索引
int j=mid+1;//初始化右边序列索引
int t=0;//指向temp数组的索引
while (i<=mid&&j<=right){
if(array[i]<=array[j]){
temp[t]=array[i];
t++;
i++;
}else {
temp[t]=array[j];
j++;
t++;
}
}
while (i<=mid){
temp[t]=array[i];
i++;
t++;
}
while (j<=right){
temp[t]=array[j];
t++;
j++;
}
//将左右两个有序序列形成的temp赋值给array
t=0;
int templeft=left;
while (templeft<=right){
array[templeft]=temp[t];
templeft++;
t++;
}
}
快速排序
快速排序重点在于数据的替换顺序,将左序列中大于pivot的元素赋值给右序列中的r;将右序列中小于pivot的元素赋值给左序列中的l;并且最后要将基准元素归位
public static void main(String[] args) {
int[] array = {
5, 1, 7, 3, 1, 6, 9, 4};
partition(array,0,array.length-1);
System.out.println(Arrays.toString(array));
}
public static void partition(int[] array,int left,int right){
if (left >= right) {
return;
}
int l = left;
int r = right;
//以排序的第一个元素为基准
int pivot = array[left];
while (l<r){
//从右往左扫描,找到第一个比基准值小的元素
while (l<r&&array[r]>=pivot){
r--;
}
//将找到的元素与左边l指向的值替换
array[l]=array[r];
//从左往右扫描,找到第一个比基准值大的元素
while (l<r&&array[l]<=pivot){
l++;
}
//将找到的元素与右边r指向的值替换
array[r]=array[l];
}
//基准归位
array[l]=pivot;
//对基准值左边的元素进行递归排序
partition(array,left,l-1);
//对基准值右边的元素进行递归排序。
partition(array,r+1,right);
}
最大字段和问题
序列(-20,11,-4,13,-5,-2),最大字段和为20
采用分治法
在计算最大字段和时主要有三种情况:
- 最大字段和在左边
- 最大字段和在右边
- 最大字段和在包含center的中间位置
故分别计算左右两边字段和,再计算中间字段和,最后进行比较即可
public static void main(String[] args){
int[] arr = {
-20,11,-4,13,-5,-2};
System.out.println(maxSubSum(arr,0,arr.length-1));
}
public static int maxSubSum(int[] arr,int left,int right){
int sum=0;
//这是递归调用必须要有的终值情况。
if(left==right){
sum=(arr[left]>0?arr[left]:0);
}
else {
int center = (left+right)/2;
//求出左序列最大字段和
int leftSum = maxSubSum(arr,left,center);
//求出右序列最大字段和
int rightSum = maxSubSum(arr,center+1,right);
//求跨前后两端的情况,从中间分别向左右两端扩展
//从中间向左扩展,注意中间往左的第一个必然包含在内
//ls用来保存左边和,必须要遍历至left,因为算的是左边子序列的最大字段和
//lefts作为辅助变量来保存运算过程中得到的值,若大与ls则赋值给ls
int ls=0,lefts=0;
for(int i=center;i>=left;i--){
lefts+=arr[i];
if(lefts>ls){
ls=lefts;
}
}
//从中间向右扩展,center的后一个必然包含在内,必须要遍历至right,因为算的是右边子序列的最大字段和
//rights作为辅助变量来保存运算过程中得到的值,若大与rs则赋值给rs
int rs=0,rights=0;
for(int i=++center;i<=right;i++){
rights+=arr[i];
if(rights>rs){
rs=rights;
}
}
sum=ls+rs;
if(sum<leftSum){
sum=leftSum;
}
if(sum<rightSum){
sum=rightSum;
}
}
return sum;
}
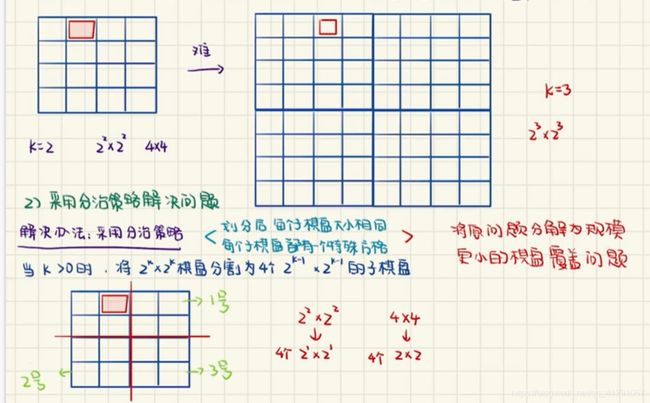
棋盘覆盖问题
重点在于涂色的方法
采用分治法,将大棋盘划分为四个小棋盘,然后进行递归:
- 第一步,处理左上角棋盘
- 第二步,处理右上角棋盘
- 第三步,处理左下角棋盘
- 第四步,处理右下角棋盘
注意在处理过程中要判断特殊块是否在此子棋盘内,若在,在递归调用;若不在,则在对应位置填充特殊块,再调用
public class Qipan {
//初始化数组
int[][] board = new int[100][100];
//L形块编号
int tile = 1;
public void Chessboard(int tr,int tc,int dr,int dc,int size){
if(size==1){
return;
}
//将棋盘分为四个子棋盘
int s=size/2;
//t用来给定当前子块的L形块的编号
int t = tile++;
//第一步处理左上角棋盘
//左上角棋盘中包含特殊块
if(dr<tr+s&&dc<tc+s){
Chessboard(tr,tc,dr,dc,s);
}else {
//若左上角棋盘中不包含特殊块,则将该子棋盘的右下角覆盖为特殊块
board[tr+s-1][tc+s-1]=t;
Chessboard(tr,tc,tr+s-1,tc+s-1,s);
}
//第二步,处理右上角棋盘
//如果右上角棋盘右特殊块
if(dc>=tc+s&&dr<tr+s){
Chessboard(tr,tc+s,dr,dc,s);
}else {
//如果右上角棋盘中不包含特殊块,则将该子棋盘的左下角覆盖为特殊块
board[tr+s-1][tc+s]=t;
Chessboard(tr,tc+s,tr+s-1,tc+s,s);
}
//第三步,处理左下角棋盘
//如果左下角棋盘有特殊块
if(dr>=tr+s&&dc<tc+s){
Chessboard(tr+s,tc,dr,dc,s);
}else {
//如果左下角棋盘无特殊块,则将该子棋盘的右上角覆盖为特殊块
board[tr+s][tc+s-1]=t;
Chessboard(tr+s,tc,tr+s,tc+s-1,s);
}
//第四步,处理右下角棋盘
//如果右下角棋盘有特殊块
if(dr>=tr+s&&dc>=tc+s){
Chessboard(tr+s,tc+s,dr,dc,s);
}else {
//如果右下角棋盘无特殊块,则将该子棋盘的左上角覆盖为特殊块
board[tr+s][tc+s]=t;
Chessboard(tr+s,tc+s,tr+s,tc+s,s);
}
}
public static void main(String[] args) {
Qipan qipan = new Qipan();
//棋盘的大小
int size = 8;
//棋盘的初始坐标
int tr=0,tc=0;
//特殊块的位置
int dr=1,dc=3;
qipan.Chessboard(tr,tc,dr,dc,size);
for(int i = 0 ;i < size;i++){
for(int j = 0 ; j < size;j++){
System.out.print(String.format("%5d",qipan.board[i][j]));
}
System.out.println();
}
}
}
最近对问题
【问题】:
最近对问题要求在包含有n个点的集合S中,找出距离最近的两个点。设 p1(x1,y1),p2(x2,y2),……,pn(xn,yn)是平面的n个点。
严格地将,最近点对可能不止一对,此例输出一对即可。
想法:
采用分治法,这道题的思想类似于最大字段和问题。通过递归求左右两边的最小值d,再将x=mid的左右两边与mid距离相差d的点集加入到集合P,求是否有两点分布在mid左右两侧使其距离最小。最后再将中将2d部分求出的距离d3与左右两边求出的距离进行比较,从而求出最小距离
public static void main(String[] args) {
int n =4;
Point[] S = new Point[n];
for(int i=0;i<n;i++){
S[i]=new Point(i,i);
}
System.out.println("最近点距离为:"+Closet(S,0,n-1));
}
public static double Closet(Point[] S,int low,int high){
double d1,d2,d3,d;
if(high-low==1){
//当集合中只有两个点时
return Distance(S[low],S[high]);
}
//当集合中只有三个点时
if(high-low==2){
d1=Distance(S[low],S[low+1]);
d2=Distance(S[low],S[high]);
d3=Distance(S[low+1],S[high]);
d = (d1>d2)?d1:d2;
if(d>d3){
d=d3;
}
return d;
}
//当集合中拥有三个以上的点时
int mid = (low+high)/2;
//递归求左右两边
d1=Closet(S,low,mid);
d2=Closet(S,mid+1,high);
Point[] P = new Point[S.length];
for(int i=0;i<S.length;i++){
P[i]=new Point();
}
int pIndex=0;
d=Math.min(d1,d2);
//将在x=mid中心线两边且距离小于d的点给到集合P
for(int i=low;i<mid&&(S[i].x-S[mid].x<d);i++){
P[pIndex]=S[i];
pIndex++;
}
for(int i = mid+1;i<=high&&(S[i].x-S[mid].x<d);i++){
P[pIndex]=S[i];
pIndex++;
}
//以下本人认为无需再排序查找最小距离,而是可以直接用暴力法,求出集合P中的最小距离
//对集合P的y坐标从小到大排序
for(int i=0;i<pIndex;i++){
for (int j=i+1;j<pIndex;j++){
if(P[i].y>P[j].y){
Point temp = P[i];
P[i]=P[j];
P[j]= temp;
}
}
}
//遍历P中所有点,查找最小距离
for(int i=0;i<pIndex;i++){
for(int j=i+1;j<pIndex;j++){
//超出y坐标的范围d
if (P[i].y-P[j].y>d){
break;
}
else {
d3=Distance(S[i],S[j]);
d=Math.min(d3,d);
}
}
}
return d;
}
public static double Distance(Point p1,Point p2){
return Math.sqrt(Math.pow(p1.x-p2.x,2)+Math.pow(p1.y-p2.y,2));
}
public static class Point{
private int x;
private int y;
//省略构造方法
}
循环赛程(分治法)
https://blog.csdn.net/wly_2014/article/details/51388263
采用分治法将所有参加比赛的选手分成两部分,n=2^k 个选手的比赛日程表就可以通过n=2^(k-1)个选手的的比赛日程表来决定。递归的执行这样的分割,直到只剩下两个选手,比赛日程表的就可以通过这样的分治策略逐步构建。
该算法的核心在于发现如下规律:
初始的2*2数组排列为【1,2】,【2,1】
每个数组分为四份,左上角的值=右下角的值,左下角的值=右上角的值,左下角的值为左上角对应的值+Math.pow(2,i-1),
i为当前循环次数,从2(2代表构成四人的赛程)开始,从k(k代表构成n=2^k人的赛程)结束
减治法
减治法:把一个大问题划分为若干个子问题,但是这些子问题不需要分别求解,只需求解其中的一个子问题,因而也无需对子问题的解进行合并
计算两个序列的中位数
问题描述:
现有两个等长的升序序列的序列A,B,试设计一个时间和空间都尽可能高效的算法,找出两个序列的中位数
算法的基本思想是:分别求出两个序列的中位数,即为a b,有下列三种情况
1:a=b;即a 为两个序列的中位数
2:a
在A1和B1中分别求出中位数,重复上述过程,得到俩个序列中只有一个元素,则较小者即为所求
注意:在利用减治法求两个序列中位数的过程中,划分后两个子序列的长度相同
若A的中位数小于B的中位数,则要使
if((s1+e1)%2==0) s1=mid1;
else s1=mid1+1;若B的中位数小于A的中位数,则要使
if((s2+e2)%2==0) s2=mid2;
else s2=mid2+1;
public static void main(String[] args) {
int[] a = {
11,13,15,17,19};
int[] b = {
2,4,10,15,20};
System.out.println(middleSerach(a,b));
}
public static int middleSerach(int[] a,int[] b){
int n = a.length;
//初始化两个序列的上下界
int s1,e1,s2,e2;
s1=0;
e1=n-1;
s2=0;
e2=n-1;
int mid1,mid2;
while (s1<e1&&s2<e2){
//分别求本次循环的子序列的两个中位数
mid1 = (s1+e1)/2;
mid2 = (s2+e2)/2;
//如果此时两个序列的中位数相同,则直接返回
if(a[mid1]==b[mid2]){
return a[mid1];
}
//如果左边序列的中位数小于右边序列的中位数
if(a[mid1]<b[mid2]){
//确保两个序列的大小相等
if((s1+e1)%2==0) s1=mid1;
else s1=mid1+1;
e2=mid2;
}
//如果右边序列的中位数小于左边序列的中位数
else {
//将右边的子序列调整为与左边子序列相等的大小
if((s2+e2)%2==0) s2=mid2;
else s2=mid2+1;
e1=mid1;
}
}
<