力扣 5.13 二分法计算完全二叉树有多少节点 双指针法删除元素
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def listOfDepth(self, tree: TreeNode) -> List[ListNode]:
root=tree
if not root:
return []
stack=[root]
res=[]
while stack:
dummy=ListNode(0)
tmp=dummy
for _ in range(len(stack)):
node=stack.pop(0)
tmp.next=ListNode(node.val)
tmp=tmp.next
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
res.append(dummy.next)
return res
222 完全二叉树的节点个数
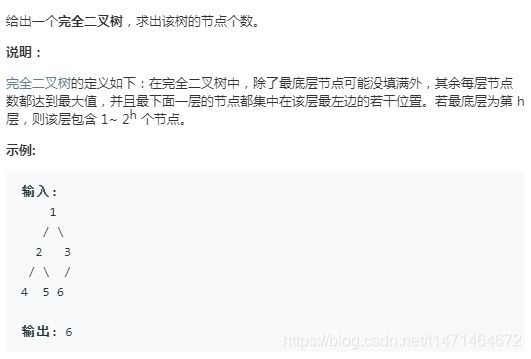
计算完全二叉树最后一层有多少节点
通过二分法,判断最后一层这个节点是否存在,
1.计算完全二叉树深度,除最后一层其余层节点数都是满的,为2d-1,d是当前层深度(0,1,2,3.。。)
2。最后一层深度为d,该层若满则 节点序号为 0-2d-1
通过二分法进行判断,假设左右边界 left=1,right=2**d-1,中点pivort=left+(right-left)//2
若中点处节点存在,则向右移动,判断右边的节点是否存在
若中点处节点不存在,则向左移动,判断左边的节点是否存在
3.如何判断中点处节点是否存在?
从根节点出发,例如pivort=4,d=3,位于01234567的右半部分,则第一步向根节点的右子树走,到达d=1
4位于4567的左半部分,则第二步向当前节点左子树走,到达d=2
4位于45的左半部分,则第三部向当前节点左子树走,到达d=3,即最后一层
判断此时节点是否为none,不为none 则说明存在
最后返回最后一层的节点数 left


# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def countNodes(self, root: TreeNode) -> int:
if not root:
return 0
def depth(root):
d=0
while root.left:
d+=1
root=root.left
return d
def isexit(index,d,root):
#例如 d=3 左0 1 2 3 右4 5 6 7
#pivort=0+7//2=3
#index=4
left,right=0,2**d-1
for _ in range(d):
pivort=left+(right-left)//2
#位于左半部分
if index<=pivort:
root=root.left
right=pivort
#位于右半部分
else:
root=root.right
left=pivort
return root is not None
#二叉树深度
d=depth(root)
if d==0:
return 1
left,right=1,2**d-1
#例如 d=3 左0 1 2 3 右4 5 6 7
#pivort=1+7//2=4
while left<=right:
pivort=left+(right-left)//2
#如果该节点存在,则索引向右移动,继续判断
if isexit(pivort,d,root):
left=pivort+1
else:
right=pivort-1
return 2**d-1+left
class Solution:
def countNodes(self, root: TreeNode) -> int:
if not root:
return 0
def dfs(root):
if not root:
return 0
return 1+dfs(root.left)+dfs(root.right)
return dfs(root)
331. 验证二叉树的前序序列化


在遍历过程中,每遇到逗号字符就更新可用槽位的数量。首先,将槽位减一(空节点和非空节点都要消耗一个槽位)。
如果当前节点是非空节点(即逗号字符前不是 #),新增两个槽位。
最后一个节点需要单独处理,因为最后一个节点后面没有逗号字符。
如果当前可用槽位是负数,那么这个先序序列就是非法的,返回 False。
如果可用槽位全部被消耗完,那么该前序序列化就是合法的:返回 slots == 0。

class Solution:
def isValidSerialization(self, preorder: str) -> bool:
slot=1
prev=None
for ch in preorder:
if ch==',':
slot-=1
if slot<0:
return False
if prev!='#':
slot+=2
prev=ch
if ch!='#':
slot+=1
else:
slot-=1
return slot==0
上下方法一致,只是下面方法需要用到 O(N) 的空间来存储前序序列化分割之后的结果数组

class Solution:
def isValidSerialization(self, preorder: str) -> bool:
slot=1
for ch in preorder.split(','):
slot-=1
if slot<0:
return False
if ch!='#':
slot+=2
return slot==0
class MyStack:
def __init__(self):
self.stack=[]
def push(self, x: int) -> None:
self.stack.append(x)
n_len=len(self.stack)
#翻转前n-1个元素,使栈顶元素始终始终位于队首,保证队列先进先出
while n_len>1:
self.stack.append(self.stack.pop(0))
n_len-=1
def pop(self) -> int:
return self.stack.pop(0)
def top(self) -> int:
return self.stack[0]
def empty(self) -> bool:
return self.stack == []
232 用栈实现队列

通过辅助栈queue2,将新入栈的数据压入到栈底,先入栈的数据放到queue2的栈顶,当queue2不为空时,弹出queue2的栈顶元素即符合队列的先入先出,当queue2为空时,将queue1的数据压入


如果使用:首先需要把 s1 中所有的元素移到 s2 中,接着把新元素压入 s2。最后把 s2 中所有的元素弹出,再把弹出的元素压入 s1。,时间复杂度和空间复杂度都是O(n),需要额外的内存来存储队列中的元素。而压入和弹出时间复杂度都是O(1),每个元素都要进行两次压入弹出,除了新元素
class MyQueue:
def __init__(self):
self.queue1=[]
self.queue2=[]
def push(self, x: int) -> None:
self.queue1.append(x)
def pop(self) -> int:
if self.queue2:
return self.queue2.pop()
else:
while self.queue1:
self.queue2.append(self.queue1.pop())
return self.queue2.pop()
def peek(self) -> int:
if self.queue2:
return self.queue2[-1]
else:
while self.queue1:
self.queue2.append(self.queue1.pop())
return self.queue2[-1]
def empty(self) -> bool:
#两个栈都存有队列元素,都需要判断
if not self.queue2 and not self.queue1:
return True
else:
return False
1090. 受标签影响的最大值


按value值从大到小选择,当标签数符合要求时,选择该值
class Solution:
def largestValsFromLabels(self, values: List[int], labels: List[int], num_wanted: int, use_limit: int) -> int:
n=len(values)
res=[]
for i in range(n):
res.append((values[i],labels[i]))
res.sort(reverse=True)
count_mit=defaultdict(int)
count=0
resum=0
for i in range(n):
if res[i][1] not in count_mit:
count_mit[res[i][1]]=1
count+=1
resum+=res[i][0]
else:
if count_mit[res[i][1]]<use_limit:
count_mit[res[i][1]]+=1
resum+=res[i][0]
count+=1
if count==num_wanted:
break
return resum
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def deleteNode(self, node):
"""
:type node: ListNode
:rtype: void Do not return anything, modify node in-place instead.
"""
node.val=node.next.val
node.next=node.next.next
203 移除链表元素

哨兵节点广泛应用于树和链表中,如伪头、伪尾、标记等,它们是纯功能的,通常不保存任何数据,其主要目的是使链表标准化,如使链表永不为空、永不无头、简化插入和删除

class Solution:
def removeElements(self, head: ListNode, val: int) -> ListNode:
dummy=ListNode(0)
dummy.next=head
tmp=dummy
cur=head
while cur:
if cur.val==val:
tmp.next=cur.next
else:
tmp=tmp.next
cur=cur.next
return dummy.next
双指针解决:
27 移除元素

请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
时间复杂度:O(n)
空间复杂度:O(1)
双指针:从前往后和从后往前,将后面不是val的值换到前面
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
if not nums:
return 0
n=len(nums)
l,r=0,n-1
while l<r:
if nums[r]==val:
r-=1
else:
nums[l],nums[r]=nums[r],nums[l]
l+=1
if nums[l]==val:
return l
else:
return l+1
26 删除排序数组中的重复元素

空间复杂度:O(1)
时间复杂度:O(n)
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
n=len(nums)
j=0
for i in range(1,n):
if nums[j]!=nums[i]:
j+=1
nums[j]=nums[i]
return j+1
80. 删除排序数组中的重复项 II

用count记录数字出现次数,因为是排序数组,当快慢指着对应数字不一致时,说明出现了新数字,count变为1,当出现重复数字时,如果出现次数满足要求,则继续赋值,否则跳过该元素
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
n=len(nums)
j=0
count=1
for i in range(1,n):
if nums[i]!=nums[j]:
count=1
j+=1
nums[j]=nums[i]
else:
count+=1
if count>2:
continue
else:
j+=1
nums[j]=nums[i]
return j+1




