6.8 力扣 二分法
509. 斐波那契数


时间复杂度O(N)
空间复杂度O(1)
class Solution:
def fib(self, N: int) -> int:
a,b=0,1
count=2
while count<=N:
a,b=b,a+b
count+=1
return b if N>=2 else N
873. 最长的斐波那契子序列的长度

递增数组,以两个数作为数列起始数据,判断第三个数是否在数组中

class Solution:
def lenLongestFibSubseq(self, A: List[int]) -> int:
s=set(A)
res=0
for i in range(len(A)):
for j in range(i+1,len(A)):
x,y=A[i],A[j]
ans=2
while x+y in s:
x,y=y,x+y
ans+=1
res=max(ans,res)
return res if res>=3 else 0
class Solution:
def isAdditiveNumber(self, num: str) -> bool:
def backtrack(num,x,y):
tmp=x+y
lent=len(str(tmp))
if num and tmp==int(num[:lent]):
num=num[lent:]
if not num:
return True
else:
return backtrack(num,y,tmp)
return False
for i in range(len(num)):
a=num[:i+1]
n_1=num[:]
num=num[i+1:]
if a[0]!='0' or int(a)==0:
for j in range(len(num)):
b=num[:j+1]
n_2=num[:]
num=num[j+1:]
if b[0]!='0' or int(b)==0:
if backtrack(num,int(a),int(b)):
return True
num=n_2[:]
num=n_1[:]
return False
93. 复原IP地址

暴力法:
分成四部分,判断每部分的合理性,每部分最多为3个字符,最大为255,且首位不能为0除非该块就是0
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
n=len(s)
num=s
res=[]
def helper(num):
if not num or (num[0]=='0' and len(num)>1) or int(num)>255:
return False
return True
for i in range(3):
for j in range(i+1,i+4):
for k in range(j+1,j+4):
if i<n and j<n and k<n:
tmp1=num[:i+1]
tmp2=num[i+1:j+1]
tmp3=num[j+1:k+1]
tmp4=num[k+1:]
if helper(tmp1) and helper(tmp2) and helper(tmp3) and helper(tmp4):
res.append(tmp1+'.'+tmp2+'.'+tmp3+'.'+tmp4)
return res
回溯法:
每一个结点可以选择截取的方法只有 3 种:截 1 位、截 2 位、截 3 位
从1位开始走到哪一步发现不成功在退回来
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
res=[]
def backtrack(count,ip,num):
if count==4:
if num=='':
#去掉最后一个‘。’
res.append(ip[:-1])
else:
return
if len(num)>0:
backtrack(count+1,ip+num[:1]+'.',num[1:])
if len(num)>1 and num[0]!='0':
backtrack(count+1,ip+num[:2]+'.',num[2:])
if len(num)>2 and int(num[:3])<256 and num[0]!='0':
backtrack(count+1,ip+num[:3]+'.',num[3:])
backtrack(0,'',s)
return res
class Solution:
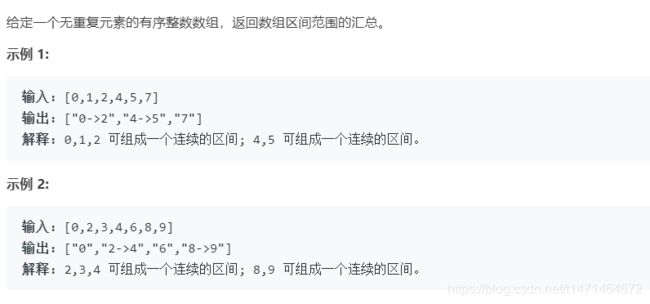
def summaryRanges(self, nums: List[int]) -> List[str]:
nums.append(float('inf'))
start,end=nums[0],nums[0]
res=[]
for i in range(1,len(nums)):
if nums[i]>end+1:
if start!=end:
res.append(str(start)+'->'+str(end))
else:
res.append(str(end))
start,end=nums[i],nums[i]
else:
end=nums[i]
return res
33. 搜索旋转排序数组

我们将数组从中间分开成左右两部分的时候,一定有一部分的数组是有序的,我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分,其中左边 [4, 5, 6] 这个部分的数组是有序的,其他也是如此
因此查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的,并根据有序的那个部分确定我们该如何改变二分搜索的上下界,因为我们能够根据有序的那部分判断出 target 在不在这个部
class Solution:
def search(self, nums: List[int], target: int) -> int:
if not nums:
return -1
left,right=0,len(nums)-1
n=len(nums)
while left<right:
mid=left+(right-left)//2
if nums[mid]==target:
return mid
#如果中间的值大于最左边的值,说明左边有序
if nums[left]<=nums[mid]:
# 如果 target 在左侧有序区间内
if nums[left]<=target<nums[mid]:
right=mid-1
else:
left=mid+1
#中间值小于最右边的值,说明右边有序
else:
#如果target在右侧有序区间内
if nums[mid]<target<=nums[right]:
left=mid+1
else:
right=mid-1
return left if nums[left]==target else -1
81. 搜索旋转排序数组 II
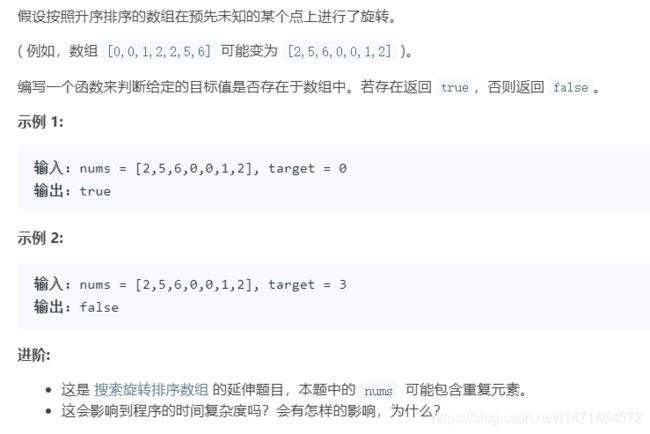
同33,存在重复元素分不清前面有序还是后面有序,可以l+=1,舍弃一个干扰项
class Solution:
def search(self, nums: List[int], target: int) -> bool:
if not nums:
return False
l,r=0,len(nums)-1
while l<r:
mid=l+(r-l)//2
if nums[mid]==target:
return True
#出现重复数据,如果左边界等于目标值,则返回True,否则舍弃这个边界
if nums[l]==nums[mid]:
if nums[l]==target:
return True
l+=1
#左边有序
elif nums[l]<nums[mid]:
#目标值位于有序数组中,则在左半部分寻找
if nums[l]<=target<nums[mid]:
r=mid-1
else:
#不在有序数组,去后半部分寻找
l=mid+1
#右边有序
else:
#位于有序数组中
if nums[mid]<target<=nums[r]:
l=mid+1
else:
r=mid-1
return True if nums[l]==target else False
class Solution:
def findMagicIndex(self, nums: List[int]) -> int:
for i in range(len(nums)):
if nums[i]==i:
return i
return -1
严格说不算二分法,因为还存在重复元素:
如果nums[mid]>mid,因为是递增数组,那么mid-nums[mid]-1之间都不是魔术索引,将从[l,mid-1]和[nums[mid],r]中继续寻找(左闭右闭)
如果nums[mid]
因为要找到最小索引,优先寻找左边数组
class Solution:
def findMagicIndex(self, nums: List[int]) -> int:
def find(l,r):
if l>r:
return -1
mid=l+(r-l)//2
if nums[mid]==mid:
return mid
idx=find(l,min(nums[mid],mid-1))
#左边没有就去查找右边
return idx if idx!=-1 else find(max(nums[mid],mid+1),r)
return find(0,len(nums)-1)
class Solution:
def minimumAbsDifference(self, arr: List[int]) -> List[List[int]]:
arr=sorted(arr)
res=[]
minl=float('inf')
for i in range(1,len(arr)):
if abs(arr[i]-arr[i-1])==minl:
res.append([arr[i-1],arr[i]])
elif abs(arr[i]-arr[i-1])<minl:
minl=abs(arr[i]-arr[i-1])
res=[[arr[i-1],arr[i]]]
return res
1366. 通过投票对团队排名


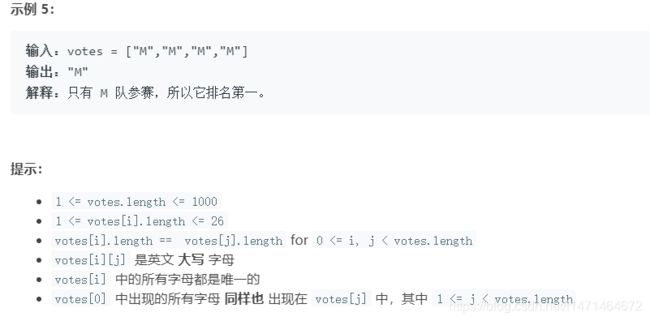
对于哈希映射中的每个键值对,键为一个在数组 votes 中出现的大写英文字母,表示一个参与排名的队伍;值为一个长度为 n 的数组 rank,表示这个队伍的排名情况,其中rank[i] 表示这个人排名为 i 的次数。
class Solution:
def rankTeams(self, votes: List[str]) -> str:
n=len(votes[0])
r=defaultdict(lambda:[0]*n)
for vo in votes:
for i,val in enumerate(vo):
r[val][i]+=1
res=sorted(r.items(),key=lambda x:(x[1],-ord(x[0])),reverse=True)
return ''.join([r for r,v in res])