数据结构P46（2-1~2-4）

2-1编写算法查找顺序表中值最小的结点，并删除该结点

#include 
#include 
typedef int DataType;
struct List
{
	int Max;//最大元素 
	int n;//实际元素个数 
	DataType *elem;//首地址 
};
typedef struct List*SeqList;//顺序表类型定义
SeqList SetNullList_Seq(int m)
{
	SeqList slist=(SeqList)malloc(sizeof(struct List));
	if(slist!=NULL)
	{
		slist->elem=(DataType*)malloc(sizeof(DataType)*m);
		//申请顺序表空间，大小为m个DataType空间 
		if(slist->elem)
		{
			slist->Max=m;//顺序表赋予的最大值 
			slist->n=0;//顺序表长度赋值为0 
			return(slist);
		}
		else free(slist);
	}
	printf("Alloc failure!\n");
	return NULL;

}

int IsNullList_seq(SeqList slist)
{
	return(slist->n==0);
} 
 
/*int InsertPre_seq(SeqList slist ,int p, DataType x)
{
	int q;
	if (slist->n>=slist->Max)//顺序表满了 
	{
		printf("overflow");
		return 0;
	}
	if(p<0||p>slist->n)//下标不存在 
	{
		printf("not exist!\n");
		return 0;
	}
	for(q=slist->n-1;q>=p;q--)
	{
		slist->elem[q+1]=slist->elem[q];
	}
	slist->elem[p]=x;
	slist->n=slist->n+1;
	return 1;
}*/

int DelIndex_seq(SeqList slist,int p)
{
  int i=0,q=0;
  for(i=0;i<slist->n;i++)
  {
  if(slist->elem[i]==p)
  {
  	for(q=i;q<slist->n-1;q++)
  	{
  		slist->elem[q]=slist->elem[q+1];
	}
	slist->n=slist->n-1;
	return 1;
  }
  	
	  
  }
}
void Print(SeqList slist)
{
	int i;
	for(i=0;i<slist->n;i++)
	{
		printf("%d\n",slist->elem[i]);
	}
}

int Insert_min(SeqList slist)
{
	int min=0,i=0;
	min=slist->elem[0];
	for(i=0;i<slist->n;i++)
	{
	if(slist->elem[i]<min)
	{
			min=slist->elem[i];
	}
	}
   return min;
}
int main()
{
	SeqList alist;
	int max,len,i,x,p;
	printf("\n please input the max value(<100) of max=");
	scanf("%d",&max);
	alist=SetNullList_Seq(max);
	printf("%d\n",IsNullList_seq(alist));
	if(alist!=NULL)
	{
		printf("\n please input the length of list len =");
		scanf("%d",&len);
		for(i=0;i<len;i++)
	  {
		scanf("%d",&x);
	    alist->elem[i]=x;
	    alist->n=i+1;
	  }
	}
	printf("The List is:\n"); 
	Print(alist);
    p=Insert_min(alist);
	DelIndex_seq(alist,p);
	printf("After deleting the min the list is :\n");
	Print(alist);
	return 1;
}
 

2-2编写算法查找单链表中值最大的结点，并将该结点移至链表尾部

#include
#include

typedef int DataType; 
struct Node
{
    DataType      data; 
    struct Node*  next;  
};
typedef struct Node  *PNode;    
typedef struct Node  *LinkList;   

void MoveMaxToTail(head);

LinkList SetNullList_Link() //设置头结点
{
    LinkList head = (LinkList)malloc(sizeof(struct Node));
    if (head != NULL) head->next = NULL;
    else printf("alloc failure");
    return head; 
}

void CreateList_Tail(struct Node* head)//利用尾插法
{
    PNode p = NULL;
    PNode q = head;
    DataType data;
    scanf("%d", &data);
    while (data != -1)
    {   
        p = (struct Node*)malloc(sizeof(struct Node));
        p->data = data;
        p->next = NULL;
        q->next = p;
        q = p;
        scanf("%d", &data);
    }
}
void  MoveMaxToTail(LinkList head)//移动到最后
{
    PNode pmax=NULL,p=NULL,pre=NULL,end=NULL;
    pmax=head->next;
    p=head->next->next;
    while(p)
    {
        if(p->data>pmax->data)
        {
            pmax=p;
        }
        p=p->next;
    }
    if(pmax->next==NULL)
    {
        return 1;
    }
    else
    {
        p=head;
        while(p)
        {
            if(p->next==pmax)
            {
                pre=p;
            }
            if(p->next==NULL)
            {
                end=p;
            }
            p=p->next;
        }
        pre->next=pmax->next;
        pmax->next=end->next;
        end->next=pmax;
    } 
    return 0;
}
void print(LinkList head)   //打印
{
    PNode  p = head->next;
    while (p)
    {
        printf("%d ", p->data);
        p = p->next;
    }
}
void DestoryList_Link(LinkList head)  //销毁链表
{
    PNode  pre = head; 
    PNode p = pre->next;
    while (p)
    {
        free(pre);
        pre = p;
        p = pre->next;
    }
    free(pre);
}

int main()
{
    LinkList head = NULL;
    head = SetNullList_Link();
    CreateList_Tail(head);
    MoveMaxToTail(head);
    print(head);
    DestoryList_Link(head);
    return 0;
}

2-3编写算法实现顺序表的就地逆序置，即利用原表的存储空间将线性表（a1.a2,…,an）逆置为（an,an-1,…,a1），并分析设计的算法时间复杂度

#include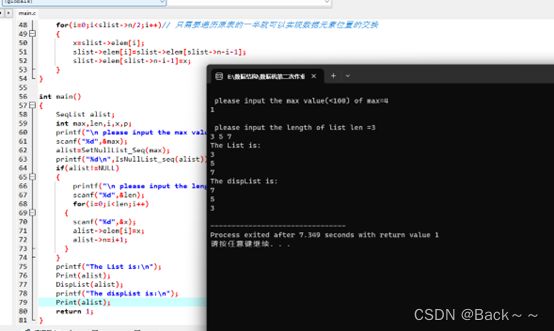 
#include 
typedef int DataType;
struct List
{
	int Max;//最大元素 
	int n;//实际元素个数 
	DataType *elem;//首地址 
};
typedef struct List*SeqList;//顺序表类型定义
SeqList SetNullList_Seq(int m)
{
	SeqList slist=(SeqList)malloc(sizeof(struct List));
	if(slist!=NULL)
	{
		slist->elem=(DataType*)malloc(sizeof(DataType)*m);
		//申请顺序表空间，大小为m个DataType空间 
		if(slist->elem)
		{
			slist->Max=m;//顺序表赋予的最大值 
			slist->n=0;//顺序表长度赋值为0 
			return(slist);
		}
		else free(slist);
	}
	printf("Alloc failure!\n");
	return NULL;

}

int IsNullList_seq(SeqList slist)
{
	return(slist->n==0);
} 
 
void Print(SeqList slist)
{
	int i;
	for(i=0;i<slist->n;i++)
	{
		printf("%d\n",slist->elem[i]);
	}
}

void DispList(SeqList slist)
{
	int i,x;
	for(i=0;i<slist->n/2;i++)// 只需要遍历原表的一半就可以实现数据元素位置的交换
	{
		x=slist->elem[i];
		slist->elem[i]=slist->elem[slist->n-i-1];
		slist->elem[slist->n-i-1]=x;
	}
}

int main()
{
	SeqList alist;
	int max,len,i,x,p;
	printf("\n please input the max value(<100) of max=");
	scanf("%d",&max);
	alist=SetNullList_Seq(max);
	printf("%d\n",IsNullList_seq(alist));
	if(alist!=NULL)
	{
		printf("\n please input the length of list len =");
		scanf("%d",&len);
		for(i=0;i<len;i++)
	  {
		scanf("%d",&x);
	    alist->elem[i]=x;
	    alist->n=i+1;
	  }
	}
	printf("The List is:\n"); 
	Print(alist);
	DispList(alist);
	printf("The dispList is:\n"); 
	Print(alist);
	return 1;
}
 

这段代码实现了一个顺序表，其中包括初始化、判断是否为空表、打印表元素、反转表元素等功能。算法时间复杂度如下：

1. SetNullList_Seq：申请顺序表空间，时间复杂度为O(1)。
2. IsNullList_seq：判断是否为空表，时间复杂度为O(1)。
3. Print：遍历表元素并打印，时间复杂度为O(n)，其中n为表的长度。
4. DispList：遍历表元素并交换位置，时间复杂度为O(n/2)，其中n为表的长度。

所以，整个代码的时间复杂度取决于最耗时的操作，即遍历表元素和交换位置。因此，整体的时间复杂度为O(n)。

2-4编写算法实现链表得到就地逆置，即利用原表的存储空间将线性表（a1,a2,…,an），逆置为（an,an-1,…,a1），并分析设计的算法时间复杂度

#include
#include

typedef int DataType; 
struct Node
{
    DataType      data; 
    struct Node*  next;  
};
typedef struct Node  *PNode;    
typedef struct Node  *LinkList;   


LinkList SetNullList_Link() //设置头结点
{
    LinkList head = (LinkList)malloc(sizeof(struct Node));
    if (head != NULL) head->next = NULL;
    else printf("alloc failure");
    return head; 
}

void CreateList_Tail(struct Node* head)//利用尾插法
{
    PNode p = NULL;
    PNode q = head;
    DataType data;
    scanf("%d", &data);
    while (data != -1)
    {   
        p = (struct Node*)malloc(sizeof(struct Node));
        p->data = data;
        p->next = NULL;
        q->next = p;
        q = p;
        scanf("%d", &data);
    }
}
void ListOppose(LinkList head)//逆置 
{
   LinkList p,t;
   p=head->next;
   while(p->next!=NULL)
   {
   	t=p->next;
   	p->next=t->next;//此时跳过了t结点元素，也就是说t结点元素脱离了链表
   	t->next=head->next; //将t结点元素放在头结点后面，即t结点元素成为第一个结点
   	head->next=t; //头结点的指针指向t
   }
}
void print(LinkList head)   //打印
{
    PNode  p = head->next;
    while (p)
    {
        printf("%d ", p->data);
        p = p->next;
    }
}
void DestoryList_Link(LinkList head)  //销毁链表
{
    PNode  pre = head; 
    PNode p = pre->next;
    while (p)
    {
        free(pre);
        pre = p;
        p = pre->next;
    }
    free(pre);
}

int main()
{
    LinkList head = NULL;
    head = SetNullList_Link();
    CreateList_Tail(head);
    print(head);
    printf("\n");
    ListOppose(head);
    print(head);
    return 0;
}

这段代码实现了一个链表，并包括了创建链表、逆置（反转）链表、打印链表和销毁链表等功能。算法的时间复杂度如下：

1. SetNullList_Link：创建头结点，时间复杂度为O(1)。
2. CreateList_Tail：利用尾插法创建链表，时间复杂度为O(n)，其中n为输入的元素个数。
3. ListOppose：逆置链表，时间复杂度为O(n)，其中n为链表的长度。
4. print：遍历链表并打印，时间复杂度为O(n)，其中n为链表的长度。
5. DestroyList_Link：销毁链表，时间复杂度为O(n)，其中n为链表的长度。

因此，整个代码的时间复杂度取决于具有最高时间复杂度的操作，即创建链表、逆置链表和销毁链表，这三者的时间复杂度均为O(n)。所以，整体的时间复杂度为O(n)。