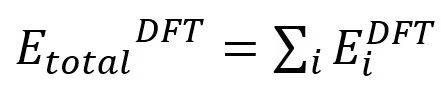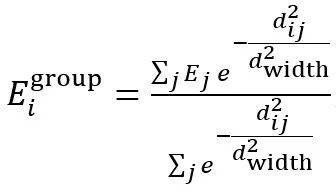New Journal of Physics：不同机器学习力场特征的准确性测试

文章信息

作者：Ting Han1, Jie Li1, Liping Liu2, Fengyu Li1, * and Lin-Wang Wang2, *

通信单位：内蒙古大学物理科学与技术学院、中国科学院半导体研究所

DOI：10.1088/1367-2630/acf2bb

研究背景

近年来，基于DFT数据的机器学习力场（machine learning force field, MLFF）发展迅速。而MLFF预测能量和力的准确性依赖于对化学环境的准确描述（特征）。目前已经提出了诸多特征方法，但是对于给定的物理问题如何选择合适的特征方法仍然是个难题。汪林望教授课题组和内蒙古大学李锋钰老师课题组使用相同的系统、相同的数据集、相同的数量特征，系统地比较了9种不同特征方法的准确性，为如何选择特征方法提供了宝贵思路。

文章简介

本文基于S、C体系，测试了9种特征类型，包括余弦特征（2-body+3-body）、高斯特征（2-body+3-body）、Moment Tensor Potential（MTP）特征、spectral neighbor analysis potential（SNAP）特征、Chebyshev多项式（DP-Chebyshev）特征和高斯多项式（DP-Gaussian）特征和原子簇展开（Atomic Cluster Expansion，ACE）特征。通过比较各特征类型对系统总能、群能、力的均方误差（RMSE）和损失函数误差，筛选出误差最小的最优特征方法为MTP，并在S、C和Cu系统中测试验证了MTP模拟的精度。

此外考虑到余弦（2-body+3-body）特征和高斯（2-body+3-body）特征对群能、总能和力模拟的较小误差，本文提出对于一个给定的系统，可以先用线性模型对不同的特征进行测试，然后将该特征集用于神经网络模型的训练。为了扩展数据集进行训练，我们采用了能量分解方法，将DFT总能分解到单个原子或者多个原子上。

01

单原子能量Ei：将DFT总能量划分为原子能量，每个原子的能量之和等于系统的总能量

由于Ei只依赖于原子i附近的原子构型，这种局部特性为MLFF模型提供了比作为总能量导数的力更加有效的数据。

02

组群多原子能量Egroup：为了减少局部能量密度分配给附近原子时的非唯一性，本文定义了一个群能（group）：

为DFT计算出的围绕中心原子i的原子能量的加权平均。

主要内容

01

使用DFT进行AIMD计算产生数据集

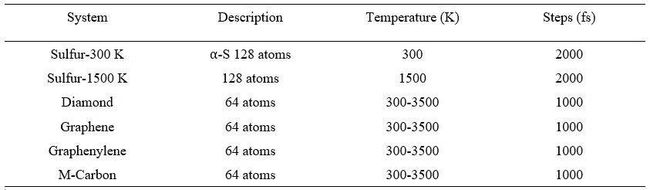
具体步骤如表1所示。计算得到3个S训练数据集：S-300 K分子动力学轨迹，S-1500 K分子动力学轨迹，S-300 K和S-1500 K轨迹组合；以及4个不同构型的C在 300-3500K的训练数据集。相应温度下的S和C结构分别如图2和3所示。

表1 S和C体系及其AIMD步骤

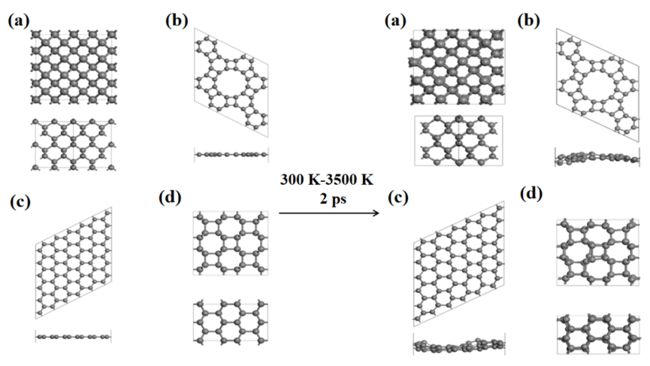
图2 S的结构: (a)初始s8环结构; (b) 300k下2 ps模拟后的结构; (c) 在1500 K下模拟2 ps后的结构

图3 (a)金刚石、(b)石墨烯、(c)类石墨烯 (d) m -碳结构在0 K和300-3500K下的俯视图和侧视图

02

通过拟合总能、群能、力和损失函数的误差比较不同特征方法的准确性

S-300 K和S-1500 K数据集（包含256000个原子能量和768000个原子力），S-300K和S-1500 K组合数据集（包含12000个原子能量和1536000个原子力）以及4种不同结构C-300-3500K数据集的总能、群能、力和损失函数的均方根误差分别如图4、5、6所示。

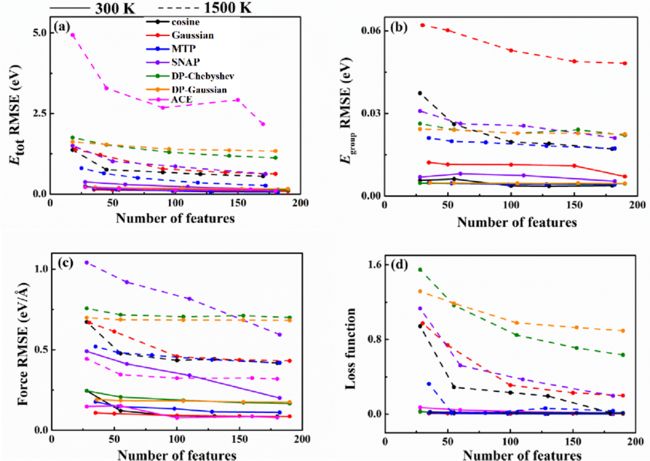
对于S-300 K体系（图4实线），MTP特征对总能的拟合效果最好（RMSE~0.060 eV）;余弦（2-body+3-body）特征对群能拟合效果最好（RMSE~0.004 eV）; 高斯特征（2-body+3-body）拟合力效果最好（RMSE~0.09 eV/Å）。总体而言，MTP特征为最佳线性模型，损失函数误差为0.002。

对于S-1500 K系统（图4虚线），各RMSE均大于S-300 K系统，群能、总能和力的均方根误差最小值分别在0.017 eV、0.263 eV和0.419 eV/Å左右，损失函数的拟合误差为0.036。除了力的最小误差由ACE特征得到，群能、总能和损失函数的最小误差均由MTP特征得到。

S-300 K和S-1500 K组合数据集与S-1500K数据集有类似的结果，MTP线性模型对总能量（RMSE~0.269 eV）、群能（RMSE~0.013 eV）和损失函数（RMSE~0.027）的误差最小，ACE特征是力精度的最佳特征类型（RMSE ~0.270 eV/Å）。但是由图5可知，组合数据集的各项误差均大于S-300 K的拟合结果，说明复杂的模拟系统对力场的拟合来说具有更高的挑战性。

图4 在S-300 K数据集（实线）和S-1500 K数据集（虚线）中，不同特征类型对于(a)总能、(b)群能、(c)力、(d)损失函数的训练误差。在python-ace包中使用了一个不同的无群能量损耗函数，故ACE结果仅在总能和力的图中显示

图5 在S-300 K和S-1500 K组合数据集中，不同特征类型对于 (a)总能、(b)群能、(c)力、(d)损失函数的训练误差。在python-ace包中使用了不同的无群能量损失函数，故ACE结果仅在总能量和力的图中显示

对于C系统，ACE模拟存在很大的错误，故只讨论其他6种特征方法的结果。如图6所示，MTP线性模型在拟合群能（RMSE~0.101 eV）、总能（RMSE~0.012 eV）方面表现出优势; 高斯（2-body）特征和余弦（3-body）特征在拟合力（RMSE~0.110 eV/Å）方面具有优势; MTP特征在损失函数上误差接近（RMSE~0.016）。

图6 在C系统的组合数据集中，不同特征类型对于 (a)总能，(b)群能，(c)力和(d)损失函数的训练误差

03

选择最优特征方法MTP，对测试集进行训练

对于S系统：使用不在训练集内的S结构，利用DFT分别在300K和1500K下进行6ps 的AIMD计算，并以最后1ps为测试集。用S-300K、S-1500K和S-300-1500K模型对两个测试集进行模拟。其与DFT计算相比，训练模型和测试集在同一温度下时，总能和力都有很好的匹配性，如图7和8所示。此外，当训练模型和测试集不在同一温度范围，模拟的误差非常大，这是由于不同温度下训练模型与测试集中的结构信息不同。

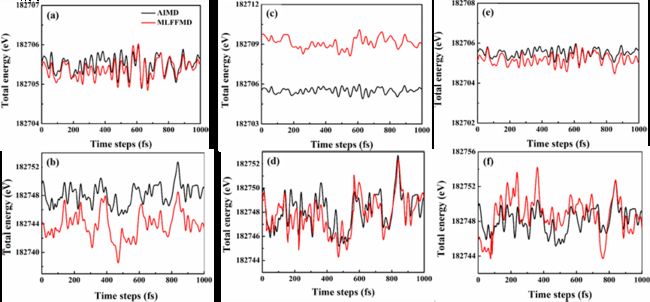
图7 基于相同轨迹的MLFF模型和DFT计算能量的比较：基于S-300K模型(a, b)、S-1500K模型(c, d)和组合模型(e, f)对S-300K-new集(a, c, e)和S-1500K-new集(b, d, f)

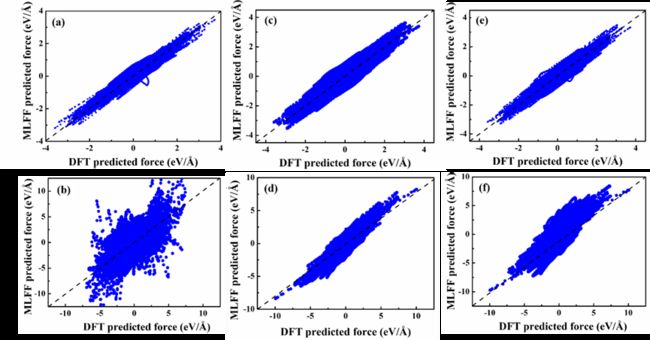
图8 基于相同轨迹的MLFF模型和DFT计算受力的比较: S-300K模型(a, b)、S-1500K模型(c, d)和组合模型(e, f)对S-300K-new (a, c, e)和S-1500K-new (b, d, f)的影响

对于C系统：选择训练集之外的C结构进行了300K 6ps的NVT AIMD模拟，以最后1ps轨迹作为测试集。如图9 (a) 和 (b) 所示，MTP-LR模型在AIMD轨迹上的总能量和力也与DFT吻合良好。C体系的总能和力的误差分别为0.22eV和0.09 eV/Å。

对除C和S以外的Cu系统：以Cu-300-1000 K的NVT 2 ps AIMD模拟作为训练集；在1000 K时对训练集之外的Cu结构进行了1 ps的NVT AIMD仿真，作为测试集。如图9 (c)和 (d) 所示，可见Cu系统的MLFF模型沿着AIMD轨迹的总能和力都与DFT结果吻合较好。其中，Cu体系的总能和力的误差分别为0.12 eV和0.05 eV/Å。

图9 在C (a, b)和Cu (c, d)两种模型中，DFT和MTP线性模型沿分子动力学轨迹的总能和力的比较