Packed Ciphertexts in LWE-based Homomorphic Encryption:解读
优质资源分享
| 学习路线指引(点击解锁) | 知识定位 | 人群定位 |
|---|---|---|
| Python实战微信订餐小程序 | 进阶级 | 本课程是python flask+微信小程序的完美结合,从项目搭建到腾讯云部署上线,打造一个全栈订餐系统。 |
| Python量化交易实战 | 入门级 | 手把手带你打造一个易扩展、更安全、效率更高的量化交易系统 |
本节内容记录阅读该论文的笔记
介绍
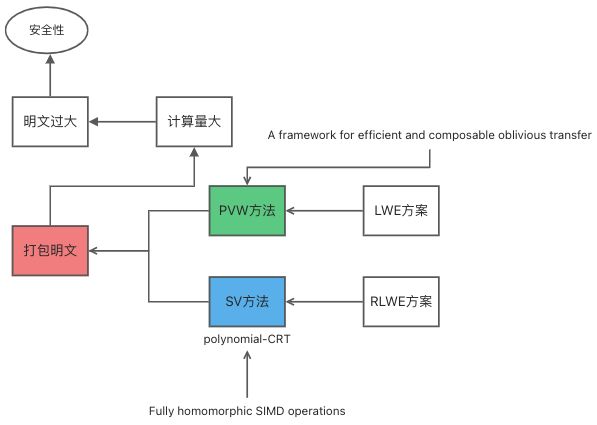
PVW:对应论文(PVW:A framework for efficient and composable oblivious transfer),打包思想就是,将多个bit明文是为一个明文向量。
SV:对应论文(SV11:Fully homomorphic SIMD operations),打包思想:将多个明文通过“编码”插入到一个多项式上,转换成多项式的计算相当于这么多明文计算。多用于基于RLWE方案的。
Regev简介
原paper:On lattices, learning with errors, random linear codes, and cryptography
加密单比特数据:系统参数q∈Zq∈Zq\in Z,明文比特b∈(0,1)b∈(0,1)b\in (0,1),私钥sss和密文ccc都是向量ZnZnZ^n,
加解密
具体加解密参考:密码算法汇总
将明文bbb加密,密文是个向量,解密的私钥sss也是向量,解密框架为: (1)加法 下面就是如何构造乘法后的正确解密: 可以看出,如果c1,c2c1,c2c_1,c_2是一个nnn维的向量的话,则c1⨂c2c1⨂c2c_1\bigotimes c_2是一个n2n2n2维的矩阵,若在此基础上再进行一次乘法,则新密文的维数为n4n4n4,可见存在一个问题:密文维数随着乘法次数而变大(指数级)。 所以需要一种方法去“降维”,即(BV11a)中给出的**重线性化技术(re-linearization)**将密文维数n2n2n^2将为nnn。 重线性化,实质上就是密钥交换技术(Key Switching),即给出两个密钥s,s′s,s′s,s’,使用密钥交换技术将密钥s′s′s’对应的密文转换为sss对应的密文。密钥交换矩阵实际上包含用s′s′s’加密的sss,这是一个矩阵(密钥交换矩阵),其实也是将s⨂ss⨂ss\bigotimes s转换为sss 前面提到原始的Regev方案是加密单bit明文,密文和密钥都是向量,这样效率较低。 可以将多个密钥sisis_i按行组成一个矩阵SSS,可以加密一个明文向量bbb,解密时:z=S.c=k.q+b.q/2+ez=S.c=k.q+b.q/2+ez=S.c=k.q+b.q/2+e,其中k,ek,ek,e是小向量。(这里的密钥有多种?) (1)打包明文的计算 只不过在乘法后执行重线性化时有些变化: 选择一个合适的密钥交换矩阵(用sisis_i加密的si⨂sisi⨂sis_i\bigotimes s_i),可以将c∗c∗c^*转换为一个新的密文c′c′c’,对应的密钥为 sisis_i。 (2)其他计算 SV方法,是通过自同构(automorphisms)实现,但是需要其他计算;而PVW是通过密钥交换实现的。 密文置换:移动密文内的slot,实现密文置换,解密后相当于明文置换。 (1)范数 具体参考:点积、张量积和范数 (2)其他符号 安全参数nnn,模数q>poly(n)q>poly(n)q>poly(n),χχ\chi表示均值为0,标准差为q/βq/βq/ \beta的离散高斯分布,β=poly(n)β=poly(n)\beta =poly(n) 问:poly()表示什么意思? 关于LWE问题的困难性,在[Regev09]中给出了证明,表明能将LWE问题通过量子规约(quantum reductions)到nnn维格上的困难问题;在[Pei09]中给出了经典规约的方法(classical reductions) 即搜索版本的LWE(search-LWE): 即判绝版本的LWE(decision-LWE): 一个基于LWE问题的公钥加密方案,这里给出了一个对称加密方案,可以通过**范型变换(generic transformations)**获得一个公钥加密方案。 范型变换? 明文空间Z2=(0,1)Z2=(0,1)Z_2=(0,1),模数qqq,安全参数n′n′n’,n=n′+1n=n′+1n=n’+1 这里介绍对称加密方案 密钥s′∈χn′s′∈χn′s’\in \chi ^{n’},明文σ∈Z2σ∈Z2\sigma\in Z_2,选取a∈Zn′qa∈Zqn′a\in Z_q^{n’},e∈χe∈χe\in \chi(小向量) 计算b=[σq/2− 解密: 上述解密可以看作:σ=⌈[ 以上基础的加密方案只需|e|< 若c1,c2c1,c2c_1,c_2是两个有效密文,分别对应的明文为b1,b2∈Z2b1,b2∈Z2b_1,b_2\in Z_2,使用的密钥是sss,从上面可知,满足: (1)加法 所以c′c′c’是b1+b2b1+b2b_1+b_2的有效加密。 对于c∗=c1⨂c2c∗=c1⨂c2c^=c_1\bigotimes c_2(n2n2n2维向量),s∗=s⨂ss∗=s⨂ss=s\bigotimes s,有乘法: 这里的e′′e″e’'是**多项式大于(polynomially (n) larger )**e1,e2e1,e2e_1,e_2的,因为k1,k2k1,k2k_1,k_2是有范围的poly(n)poly(n)poly(n) 这里如何理解:polynomially larger? 下面将2/q.c∗2/q.c∗2/q.c^四舍五入为整数向量,即求⌈2/q.c∗⌋=2/q.c∗+e⌈2/q.c∗⌋=2/q.c∗+e\left \lceil 2/q.c^\right \rfloor=2/q.c^*+e,其中eee是舍入误差,||e||∞≤1/2||e||∞≤1/2||e||_{\infty} \leq 1/2,则: 其中e∗e∗e*是误差集合,k∗k∗k是一些整数,由于s∗=s⨂ss∗=s⨂ss^=s\bigotimes s和eee中元素很小,所以 最后令c′′=⌈2/q.c∗⌋qc″=⌈2/q.c∗⌋qc’'=\left \lceil 2/q.c^*\right \rfloor_q,满足: 所以c′′c″c’'是b1b2b1b2b_1b_2的有效加密,密钥为s∗=s⨂ss∗=s⨂ss^*=s\bigotimes s。 上面可以看出,密文相乘后,维数扩张严重(指数级)。在【BV11a】中给出了方法-密钥交换技术,作用就是降维。 从上面密钥交换的简单介绍中,可知道主要功能:将一个维数为n2n2n^2维的密文c′c′c’,对应的密钥为s′s′s’,转换为一个新的密文ccc,其维数为nnn,对应的密钥为sss。 下面介绍一种密钥交换的变体技术,相对更加简单。 (1)密钥交换需要一个密钥交换矩阵 (2)然后将高维密文转换为低维密文 总的来说,对于维数为nnn的新密文ccc,满足 从上面可以看出,1bit的明文加密后的密文是n′+1n′+1n’+1维,在【PVW08】中给出了一种“打包”明文的方法,提升计算效率,简单点说就是,m′m′m’bit的明文加密后的密文是m=n′+m′m=n′+m′m=n’+m’维 这里选取m′m′m’个向量(m′m′m’个大小为n′n′n’的向量),即si∈χn′si∈χn′s_i\in \chi^{n’},将其组成一个m′.n′m′.n′m’.n’的矩阵S′S′S’(按行),之前使用的是n′+1n′+1n’+1维的密钥向量s=(1|s′)s=(1|s′)s=(1|s’),现在使用的是m′.mm′.mm’.m的密钥矩阵S=(I|S′)S=(I|S′)S=(I|S’),其中,III是i个m′.m′m′.m′m’.m’的单位矩阵。 上面是密钥生成,下面开始加解密: (1)加密 (2)解密 总的来说,对于密文ccc,对应密钥为SSS,有效的解密为: (3)同态计算 密文相加c′=[c1+c2]qc′=[c1+c2]qc’=[c_1+c_2]_q,分别对应于明文(b1⨁b2)(b1⨁b2)(b_1\bigoplus b_2)。 密文相乘c′′=[2/q.c1⨂c2]qc″=[2/q.c1⨂c2]qc’‘=[2/q.c_1 \bigotimes c_2]_q,分别对应明文b1⨀b2∈Zm′2b1⨀b2∈Z2m′b_1\bigodot b_2\in Z_2^{m’}(bitwise product,按位乘)。 密钥交换是需要“计算密钥”(public key key-switching gadgets)的,利用计算密钥使得s∗i−>sisi∗−>sis_i*->s_i,但是这样对于每一个密文转换(c′′−>c)(c″−>c)(c’‘->c),都需要一个计算密钥,我们想要的是使用一个计算密钥,将高维密文c′′c″c’'(对应的密钥为s∗s∗s*),转换为一个低维密文ccc(对应密钥为sss)。 计算密钥能得到密钥交换矩阵WWW 密钥交换的“计算密钥”可以看作是用密钥sss加密s∗s∗s*构成的。具体来看,就是把sisis_i作为密钥,加密所有的s∗isi∗s_i*。 这里的密钥交换矩阵WWW,满足SW=S∗+E(modq)SW=S∗+E(modq)SW=S*+E(mod q),其中EEE是误差矩阵。具体说,m=n′+m′m=n′+m′m=n’+m’,可以利用W∈Qm.m2W∈Qm.m2W\in Q{m.m2},将S∗∈Zm′.m2S∗∈Zm′.m2S^*\in Z{m’.m2}对应的密文转换为S=(I|S′)∈Zm′.mS=(I|S′)∈Zm′.mS=(I|S’)\in Z^{m’.m}对应的密文,那WWW如何求呢? 对于j∈(1,2,…,m2)j∈(1,2,…,m2)j\in (1,2,…,m^2),s˜j∈Zm′s~j∈Zm′\widetilde{s}_j \in Z{m’}组成矩阵S∗S∗S*(按列),ai∈Zn′Qai∈ZQn′a_i\in Z_Q^{n’}组成矩阵WWW(按行),ej∈Zm′ej∈Zm′e_j\in Z{m’}是误差向量,计算dj=[2l.s˜j−S′aj+ej]Qdj=[2l.s~j−S′aj+ej]Qd_j=[2l.\widetilde{s}_j-S’a_j+e_j]_Q,输出wj=(dj|aj)T/2l∈Qmwj=(dj|aj)T/2l∈Qmw_j=(d_j|a_j)T/2l\in Q^m,按行组成WWW。 djdjd_j也可以表示为dj=2l.s˜j−S′aj+ej+kQdj=2l.s~j−S′aj+ej+kQd_j=2^l.\widetilde{s}_j-S’a_j+e_j+kQ,则满足: 也即是: 给出一个高维密文c∗c∗c^,对应密钥为S∗S∗S,利用密钥交换矩阵WWW,可得低维新密文c=⌈Wc∗⌋qc=⌈Wc∗⌋qc=\left \lceil Wc^* \right \rfloor_q,对应密钥为SSS,且解密后的明文是一样的。 若对于S∗.c∗=k∗.q+b(q/2)+e∗S∗.c∗=k∗.q+b(q/2)+e∗S*.c*=k*.q+b(q/2)+e和S.c=k.q+b(q/2)+eS.c=k.q+b(q/2)+eS.c=k.q+b(q/2)+e,需要满足k∗,e∗,k,e< 在一个Leveled-FHE方案中,需要提前生成多个互相独立的密钥矩阵SkSkS_k,使得在每次乘法后执行密钥交换,转换为新的密钥,所以在该方案中,乘法的次数就受限于密钥的个数。 安全性是基于LWE问题。上面的引理是在S∗S∗S*和SSS是独立关系的前提下,假如S∗S∗S*和SSS不是独立的,那这就依赖于“循环安全假设”(circular security)了。 使用以上技术,可以实现“压缩”版的SIMD同态计算,就是每计算一次相当于计算多次! 什么是密文置换? 规定一种置换映射π()π()\pi(): 对于一个密文ccc,对应密钥为SSS,解密后的密文为b∈Zm′2b∈Z2m′b\in Z_2^{m’},将其作用在π()π()\pi()上,得到c′=π©c′=π©c’=\pi©。用SSS去解密c′c′c’,会得到π(b)π(b)\pi(b)。 使用密钥交换实现很简单:准备一个密钥交换矩阵WWW,可以得到将(π(S)−>S)(π(S)−>S)(\pi(S)->S) 本文基于LWE问题,设计了一种PVW变体的压缩明文方案,这就类似于SV压缩方案,在环上的便利。 (1)基于多项上环比实数环的方案具有更好的渐进效率(asymptotic efficiency) 1、【论文阅读笔记】-针对RSA的短解密指数的密码学分析(Cryptanalysis of Short RSA Secret Exponents)
z=
同态计算
Regev本身支持同态加法计算,即E(b1+b2)=c1+c2(modq)E(b1+b2)=c1+c2(modq)E(b_1+b_2)=c_1+c_2(mod q)。
(2)乘法
在该paper:(BV11a:Efficient fully homomorphic encryption from (standard) LWE)中给出同态乘法运算:
这里的“乘法”是张量积,满足:E(b1.b2)=(c1⨂c2E(b1.b2)=(c1⨂c2E(b_1.b_2)=(c_1\bigotimes c_2),并满足
c∗=⌈2/q.(c1⨂c2)⌋c∗=⌈2/q.(c1⨂c2)⌋c^=\left \lceil 2/q.(c_1\bigotimes c_2)\right \rfloor
则:z∗=打包“压缩”明文
还是和上面说的类似,加法(mod q),乘法通过张量积。
假设c∗c∗c^*是一个高维的“打包”密文,对于每iii个明文bib′ibibi′b_ib_i’,对应的密钥为si⨂sisi⨂sis_i\bigotimes s_i,现在如何进行重线性化呢?
可以在“打包”明文基础上实现SIMD同态计算、密文置换(permutation),并且使用PVW方法进行密文置换比使用SV方法更有优势。基础
符号
||v||1||v||1||v||_1:欧式范数
||v||∞||v||∞||v||_{\infty }:无穷范数
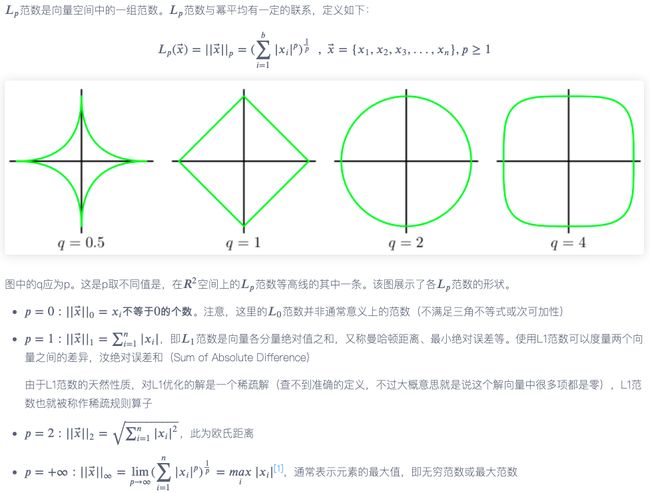
ZqZqZ_q:表示范围在[−q/2,+q/2][−q/2,+q/2][-q/2,+q/2]内的整数
[a]q[a]q[a]_q:表示amodqamodqa mod q
⌈a⌋⌈a⌋\left \lceil a \right \rfloor:表示四舍五入
⌈a⌋q⌈a⌋q\left \lceil a \right \rfloor_q:表示[⌈a⌋]q[⌈a⌋]q\left [\left \lceil a \right \rfloor \right ]_qLWE问题
SLWE
对于(ai∈Znq,bi=[DLWE
给出Regev方案
密钥生成
加解密
计算d=[b+
解密成功的关键在于||e||∞<
同态计算
对于c′=[c1+c+2]c′=[c1+c+2]c’=[c_1+c+2],满足
(2)乘法
在【BV11】和【Bra12】中给出了Regev的乘法同态。

见参考【1】

在这里的意思就是e′′/e1e″/e1e’‘/e_1或者e′′/e2e″/e2e’'/e_2是有范围的!
![]()
![]()
密钥交换
密钥交换(s∗−>ss∗−>ss*->s)可以看成:在密钥sss下加密的s∗s∗s,详细点说:对于每一个s∗[i]s∗[i]s^[i],构造一个公开的“计算密钥”wiwiw_i(rational “ciphertext” ),满足:
给出一个n2n2n2维密文向量c∗c∗c满足:
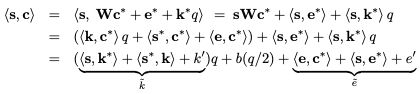
“打包”明文的计算
介绍
对于明文b∈Zm′2b∈Z2m′b\in Z_2^{m’},即明文是一个比特串(向量),随机取向量z∈Zn′qz∈Zqn′z\in Z_q^{n’},误差向量x∈χmx∈χmx\in \chi ^m,计算d=[b.q/2−S′a+x]qd=[b.q/2−S′a+x]qd=[b.q/2-S’a+x]_q,输出密文向量c=(d|a)∈Zmqc=(d|a)∈Zqmc=(d|a)\in Z_q^m。
计算Sc=d+S′a=b.q/2+x(modq)Sc=d+S′a=b.q/2+x(modq)Sc=d+S’a=b.q/2+x(mod q),对于计算结果(向量),观察其中每个元素,若元素大于q/4q/4q/4,则为1,否则为0。其中xxx中的每个元素远小于qqq,解密也可以表示为b=⌈[Sc]q/(q/2)⌋2b=⌈[Sc]q/(q/2)⌋2b=\left \lceil [Sc]_q/(q/2) \right \rfloor_2。
![]()
其中∥k∥∞,∥x∥∞<
从加解密来看,对于两个密文c1,c2∈Zmqc1,c2∈Zqmc_1,c_2\in Z_q^m,分别对应明文是b1,b2∈Zm′2b1,b2∈Z2m′b_1,b_2\in Z_2^{m’},密钥为S∈Zm′.mqS∈Zqm′.mS\in Z_q^{m’.m}。密钥交换

上面比较重要的内容是:想要安全性高,那就要提升模数n′n′n’的大小。
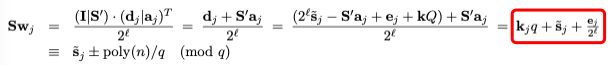
![]()
其中整数矩阵KKK和误差矩阵EEE满足∥E∥∞≤poly(n)/q‖E‖∞≤poly(n)/q\left|E \right|_{\infty }\leq poly(n)/q总结
密文置换
在密文计算量更大的需求下,“压缩”实为是一种好的实现,对于密文置换,可以利用密钥交换实现。介绍
对于π©π©\pi©,对应密钥为π(S)π(S)\pi(S),解密明文为π(b)π(b)\pi(b),使用密钥交换,将其转换为一个新的密文c′c′c’,对应的密钥为SSS,解密明文为π(b)π(b)\pi(b)。总结
基于整数环和多项式环上的对比
(2)两种情况下密文的大小大致相同:多项式环上的密文是一个多项式,其中包含O(n)O(n)O(n)个整数。
(3)对于密文乘法(tensor product multiplication),基于整数的密文大小扩大为O(n2)O(n2)O(n^2)倍,基于多项式的密文大小仍是O(n)O(n)O(n)。
(4)对于重线性化,基于整数的密钥交换矩阵为O(n3)O(n3)O(n^3),基于多项式的密钥交换矩阵为O(n)O(n)O(n),基于整数上的计算会产生更多开销。
(5)对于密文中的“slot”个数,基于多项式的是由底层环结构决定的,基于整数的slot个数可以任意设置。
(6)在密文置换上,基于整数的比基于多项式更优。
(7)对于密钥交换,基于整数的比基于多项式的更方便和高效。参考
2、范数||x||(norm)笔记