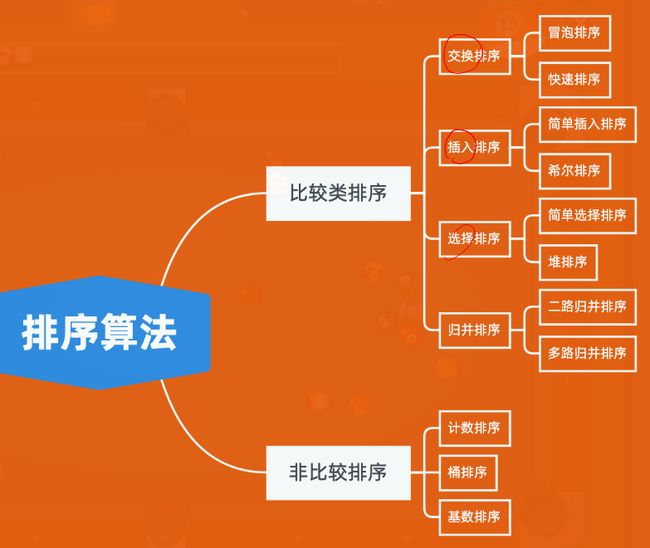
第九课 排序
文章目录
- 第九课 排序
-
- 排序算法
- lc912.排序数组--中等
-
- 题目描述
- 代码展示
- lc1122.数组的相对排序--简单
-
- 题目描述
- 代码展示
- lc56.合并区间--中等
-
- 题目描述
- 代码展示
- lc215.数组中的第k个最大元素--中等
-
- 题目描述
- 代码展示
- acwing104.货仓选址--简单
-
- 题目描述
- 代码展示
- lc493.翻转树--困难
-
- 题目描述
- 代码展示
- lc327.区间个数--困难
-
- 题目描述
- 代码展示
第九课 排序
排序算法
快速排序算法动画演示_哔哩哔哩_bilibili
lc912.排序数组–中等
题目描述
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0]
输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 5 * 104-5 * 104 <= nums[i] <= 5 * 104
代码展示
class Solution {
public: //堆排序——不会超时
vector<int> sortArray(vector<int>& nums) {
heapSort(nums);
return nums;
}
private:
void heapify(vector<int>& nums, int n, int i) {
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < n && nums[left] > nums[largest])
largest = left;
if (right < n && nums[right] > nums[largest])
largest = right;
if (largest != i) {
swap(nums[i], nums[largest]);
heapify(nums, n, largest);
}
}
void heapSort(vector<int>& nums) {
int n = nums.size();
// 建立最大堆
for (int i = n / 2 - 1; i >= 0; i--)
heapify(nums, n, i);
// 逐步提取元素
for (int i = n - 1; i > 0; i--) {
swap(nums[0], nums[i]);
heapify(nums, i, 0);
}
}
};
class Solution {
public: //归并排序也可以
vector<int> sortArray(vector<int>& nums) {
vector<int> tmp(nums.size());
mergeSort(nums, tmp, 0, nums.size() - 1);
return nums;
}
private:
void merge(vector<int>& nums, vector<int>& tmp, int left, int mid, int right) {
int i = left;
int j = mid + 1;
int k = left;
while (i <= mid && j <= right) {
if (nums[i] <= nums[j]) {
tmp[k++] = nums[i++];
} else {
tmp[k++] = nums[j++];
}
}
while (i <= mid) {
tmp[k++] = nums[i++];
}
while (j <= right) {
tmp[k++] = nums[j++];
}
for (int l = left; l <= right; l++) {
nums[l] = tmp[l];
}
}
void mergeSort(vector<int>& nums, vector<int>& tmp, int left, int right) {
if (left < right) {
int mid = left + (right - left) / 2;
mergeSort(nums, tmp, left, mid);
mergeSort(nums, tmp, mid + 1, right);
merge(nums, tmp, left, mid, right);
}
}
};
lc1122.数组的相对排序–简单
题目描述
给你两个数组,arr1 和 arr2,arr2 中的元素各不相同,arr2 中的每个元素都出现在 arr1 中。
对 arr1 中的元素进行排序,使 arr1 中项的相对顺序和 arr2 中的相对顺序相同。未在 arr2 中出现过的元素需要按照升序放在 arr1 的末尾。
示例 1:
输入:arr1 = [2,3,1,3,2,4,6,7,9,2,19], arr2 = [2,1,4,3,9,6]
输出:[2,2,2,1,4,3,3,9,6,7,19]
示例 2:
输入:arr1 = [28,6,22,8,44,17], arr2 = [22,28,8,6]
输出:[22,28,8,6,17,44]
提示:
1 <= arr1.length, arr2.length <= 10000 <= arr1[i], arr2[i] <= 1000arr2中的元素arr2[i]各不相同arr2中的每个元素arr2[i]都出现在arr1中
代码展示
你可以使用自定义比较函数来解决这个问题,首先建立一个哈希表,将arr2中的元素与其对应的位置映射起来。然后,使用自定义的比较函数对arr1进行排序,排序规则如下:
- 如果a和b都在arr2中,比较它们在arr2中的位置,位置靠前的元素排在前面。
- 如果a和b都不在arr2中,直接比较它们的大小。
以下是示例代码:
class Solution {
public:
vector<int> relativeSortArray(vector<int>& arr1, vector<int>& arr2) {
unordered_map<int, int> position;
for (int i = 0; i < arr2.size(); i++) {
position[arr2[i]] = i;
}
sort(arr1.begin(), arr1.end(), [&](int a, int b) {
if (position.count(a) && position.count(b)) {
return position[a] < position[b];
} else if (position.count(a)) {
return true;
} else if (position.count(b)) {
return false;
} else {
return a < b;
}
});
return arr1;
}
};
这段代码首先建立了一个哈希表 position,将arr2中的元素与其对应的位置映射起来。然后,使用自定义的比较函数对arr1进行排序,按照上述规则进行比较。这样就能够保证arr1中的元素按照arr2中的相对顺序排列,未在arr2中出现的元素按照升序排在末尾。
如果你想自己实现排序函数,你可以使用计数排序的方法,首先统计arr1中每个元素的出现次数,然后根据arr2的顺序构建排序后的结果。
以下是示例代码:
class Solution {
public:
vector<int> relativeSortArray(vector<int>& arr1, vector<int>& arr2) {
// 统计arr1中每个元素的出现次数
vector<int> count(1001, 0);
for (int num : arr1) {
count[num]++;
}
vector<int> result;
// 根据arr2的顺序构建排序后的结果
for (int num : arr2) {
while (count[num] > 0) {
result.push_back(num);
count[num]--;
}
}
// 处理arr2中没有的元素
for (int i = 0; i <= 1000; i++) {
while (count[i] > 0) {
result.push_back(i);
count[i]--;
}
}
return result;
}
};
这段代码首先使用 count 数组统计了arr1中每个元素的出现次数。然后,根据arr2的顺序构建了排序后的结果,并将结果存储在 result 数组中。最后,处理arr2中没有的元素,将它们按照升序添加到 result 数组中。
这样就能够实现按照arr2的相对顺序对arr1进行排序。
lc56.合并区间–中等
题目描述
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
提示:
1 <= intervals.length <= 104intervals[i].length == 20 <= starti <= endi <= 104
代码展示
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if (intervals.empty()) {
return {};
}
// 对区间进行双关键字排序(按左端点升序,右端点升序)
sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b) {
return a[0] == b[0] ? a[1] < b[1] : a[0] < b[0];
});
vector<vector<int>> mergedIntervals;
mergedIntervals.push_back(intervals[0]);
// 扫描合并
for (int i = 1; i < intervals.size(); i++) {
vector<int>& currentInterval = intervals[i];
vector<int>& previousInterval = mergedIntervals.back();
if (currentInterval[0] <= previousInterval[1]) {
// 当前区间和前一个区间重叠,合并区间
previousInterval[1] = max(previousInterval[1], currentInterval[1]);
} else {
// 当前区间和前一个区间不重叠,将当前区间添加到结果中
mergedIntervals.push_back(currentInterval);
}
}
return mergedIntervals;
}
};
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
/*[1, 5] [2, 6] [3, 4] [6, 10] [11 12]
1 2 3 4 5 6 7 8 9 10 11 12
1 1 1 1 1
1 1 1 1 1
1 1
1 1 1 1 1
1 1
+1 -1
+1 -1
+1-1
+1 -1
+1 -1
count: 0
把从1覆盖到5这个区间,看作2个事件:
(a) 在1处,有一个事件:开始覆盖(次数+1)
(b) 在5处,有一个事件:结束覆盖(次数-1)
*/
// 产生2n个事件
// 时间位置,时间情况(+1/-1)
vector<pair<int,int>> events;
for (vector<int>& interval : intervals) {
// 差分
events.push_back(make_pair(interval[0], 1));
events.push_back(make_pair(interval[1], -1));
}
sort(events.begin(), events.end(),
[](pair<int,int>& a, pair<int,int>& b) {
// 1 在 -1 之前(如果差分是闭区间[1,5]而不是前闭后开[1,6)的话
return a.first < b.first || (a.first == b.first && a.second > b.second);
});
int count = 0;
int left;
vector<vector<int>> ans;
for (pair<int,int>& event : events) {
if (count == 0) // 加之前是0,加之后是非0
left = event.first; // 一个段的产生
count += event.second;
if (count == 0) // 非零变零,一个段的结束
ans.push_back({left, event.first});
}
return ans;
}
};
lc215.数组中的第k个最大元素–中等
题目描述
给定整数数组 nums 和整数 k,请返回数组中第 **k** 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示:
1 <= k <= nums.length <= 105-104 <= nums[i] <= 104
代码展示
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int left = 0;
int right = nums.size() - 1;
while (left <= right) {
int pivotIndex = partition(nums, left, right);
if (pivotIndex == k - 1) {
return nums[pivotIndex];
} else if (pivotIndex < k - 1) {
left = pivotIndex + 1;
} else {
right = pivotIndex - 1;
}
}
return -1; // 如果输入无效或 k 超出范围,可以返回一个特殊值
}
int partition(vector<int>& nums, int left, int right) {
int pivot = nums[left];
int l = left + 1;
int r = right;
while (l <= r) {
if (nums[l] < pivot && nums[r] > pivot) {
swap(nums[l++], nums[r--]);
}
if (nums[l] >= pivot) l++;
if (nums[r] <= pivot) r--;
}
swap(nums[left], nums[r]);
return r;
}
};
acwing104.货仓选址–简单
题目描述
代码展示
#include lc493.翻转树–困难
题目描述
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个*重要翻转对*。
你需要返回给定数组中的重要翻转对的数量。
示例 1:
输入: [1,3,2,3,1]
输出: 2
示例 2:
输入: [2,4,3,5,1]
输出: 3
注意:
- 给定数组的长度不会超过
50000。 - 输入数组中的所有数字都在32位整数的表示范围内。
代码展示
class Solution {
public:
int reversePairs(vector<int>& nums) {
int n = nums.size();
if (n <= 1) {
return 0; // 如果数组长度小于等于1,不存在翻转对
}
vector<int> temp(n); // 用于归并排序的辅助数组
return mergeSort(nums, temp, 0, n - 1);
}
int mergeSort(vector<int>& nums, vector<int>& temp, int left, int right) {
if (left >= right) {
return 0; // 当子数组长度为1时,不再拆分,返回0
}
int mid = left + (right - left) / 2;
int count = mergeSort(nums, temp, left, mid) + mergeSort(nums, temp, mid + 1, right);
int i = left; // 左子数组的起始位置
int j = mid + 1; // 右子数组的起始位置
int k = left; // 辅助数组的起始位置
// 统计翻转对的数量
while (i <= mid) {
while (j <= right && static_cast<long long>(nums[i]) > 2LL * nums[j]) {
j++;
}
count += (j - (mid + 1)); // 统计右子数组中满足条件的元素数量
i++;
}
// 归并排序合并两个子数组,并保持有序性
i = left;
j = mid + 1;
while (i <= mid && j <= right) {
if (nums[i] <= nums[j]) {
temp[k++] = nums[i++];
} else {
temp[k++] = nums[j++];
}
}
while (i <= mid) {
temp[k++] = nums[i++];
}
while (j <= right) {
temp[k++] = nums[j++];
}
for (i = left; i <= right; i++) {
nums[i] = temp[i];
}
return count;
}
};
要解决这个问题,可以使用归并排序的思想来统计重要翻转对的数量。具体步骤如下:
- 将原始数组拆分成两个子数组。
- 分别对两个子数组进行排序。
- 遍历其中一个子数组的元素,并查找另一个子数组中满足条件的元素,以统计重要翻转对的数量。
- 合并两个子数组时,继续维护它们的有序性。
这段代码首先将原始数组拆分成两个子数组,然后对这两个子数组分别进行归并排序。在归并排序的过程中,统计满足条件的翻转对的数量,并在合并时维护子数组的有序性。最终,返回翻转对的数量。时间复杂度为O(n*log(n))。
lc327.区间个数–困难
题目描述
给你一个整数数组 nums 以及两个整数 lower 和 upper 。求数组中,值位于范围 [lower, upper] (包含 lower 和 upper)之内的 区间和的个数 。
区间和 S(i, j) 表示在 nums 中,位置从 i 到 j 的元素之和,包含 i 和 j (i ≤ j)。
示例 1:
输入:nums = [-2,5,-1], lower = -2, upper = 2
输出:3
解释:存在三个区间:[0,0]、[2,2] 和 [0,2] ,对应的区间和分别是:-2 、-1 、2 。
示例 2:
输入:nums = [0], lower = 0, upper = 0
输出:1
提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 1-105 <= lower <= upper <= 105- 题目数据保证答案是一个 32 位 的整数
代码展示
class Solution {
public:
int countRangeSum(vector<int>& nums, int lower, int upper) {
int n = nums.size();
vector<long long> prefixSum(n + 1, 0);
for (int i = 0; i < n; i++) {
prefixSum[i + 1] = prefixSum[i] + nums[i];
}
return countAndMerge(prefixSum, 0, n, lower, upper);
}
int countAndMerge(vector<long long>& prefixSum, int left, int right, int lower, int upper) {
if (left == right) {
return 0; // 递归结束条件
}
int mid = left + (right - left) / 2;
int count = countAndMerge(prefixSum, left, mid, lower, upper) +
countAndMerge(prefixSum, mid + 1, right, lower, upper);
int i = left;
int j = mid + 1;
int k = mid + 1;
while (i <= mid) {
while (j <= right && prefixSum[j] - prefixSum[i] < lower) {
j++;
}
while (k <= right && prefixSum[k] - prefixSum[i] <= upper) {
k++;
}
count += (k - j);
i++;
}
// 归并排序
vector<long long> sorted(right - left + 1, 0);
int p1 = left;
int p2 = mid + 1;
int p = 0;
while (p1 <= mid || p2 <= right) {
if (p1 > mid) {
sorted[p++] = prefixSum[p2++];
} else if (p2 > right) {
sorted[p++] = prefixSum[p1++];
} else {
if (prefixSum[p1] < prefixSum[p2]) {
sorted[p++] = prefixSum[p1++];
} else {
sorted[p++] = prefixSum[p2++];
}
}
}
for (int i = 0; i < sorted.size(); i++) {
prefixSum[left + i] = sorted[i];
}
return count;
}
};
要解决这个问题,可以使用归并排序和前缀和的结合方法。具体步骤如下:
- 计算前缀和数组
prefixSum,其中prefixSum[i]表示nums数组中前i个元素的和。 - 定义一个递归函数
countAndMerge用于统计区间和个数并归并排序prefixSum数组。 - 在
countAndMerge函数中,首先计算中间索引mid,然后递归计算左半部分和右半部分的区间和个数。 - 接下来,合并左半部分和右半部分的区间和,统计符合要求的区间和个数。
- 最后,返回区间和个数。
这段代码首先计算前缀和数组 prefixSum,然后使用递归函数 countAndMerge 统计区间和个数并归并排序 prefixSum 数组。在 countAndMerge 函数中,通过归并排序合并左半部分和右半部分的区间和,同时统计满足要求的区间和个数。最终,返回区间和个数。时间复杂度为O(n*log(n))。