有限元分析-材料非线性(一) 弹塑性
1. 前言
结构非线性的内容包含三部分,分别是几何非线性、材料非线性和状态非线性,几何非线性及其相关知识的补充已经完结,从本章开始进行材料非线性内容的叙述。材料非线性部分内容较多,涉及到很多材料的本构模型及相应的案例,因此分为多个章节。本章先对基本理论进行介绍,之后开始材料非线性的第一部分—弹塑性。
材料非线性在工程领域应用广泛,主要有塑性成形,结构密封,橡胶圈减震等等。ANSYS Workbench中也提供了多种非线性材料模型,包括弹塑性、粘塑性、超弹性、橡胶、蠕变等等。那什么是材料的非线性呢?以几何非线性为例,当力和变形的关系使结构刚度发生变化,即刚度K是变形的函数时,称为几何非线性。材料非线性也是如此,不过这时的非线性关系体现在应力和应变之间。
ANSYS中的材料非线性主要以下几种:
率无关塑性:“率”是指应变率,率无关可以解释为材料的响应和载荷速率或变形速率无关。所以率无关塑性可以简单理解为,材料塑性应变的发生跟时间没有关系!低温(小于¼或⅓的熔点)时大多数材料呈现率无关行为,我们本文要讲的弹塑性就是率无关塑性;
率相关塑性:同理,率相关就是材料的响应跟时间有关系,即材料的塑性应变是加载速度和时间的函数,粘塑性就属于率相关塑性;
蠕变:材料的蠕变行为也是率相关的,所产生的的应变随时间推移而发展,但是蠕变的时间尺度要比率相关塑性大得多;
非线性弹性:材料的应力应变关系是非线性的,但所有的应变都可以恢复;
超弹性:应力应变关系由应变能密度势函数定义,用于模拟橡胶和泡沫等材料,所有应变可恢复;
粘弹性:也是一种率相关材料,这种材料的应变中包含弹性应变和粘性应变;
混凝土:可以模拟断裂和压碎;
膨胀:材料在中子流作用下的体积扩大效应;
在材料非线性专题中,我们将对上面这些特性进行详细描述。
2. 基础理论
本节对弹塑性材料分析涉及到的基本理论进行介绍,首先是材料的应力-应变曲线,这部分内容在材料力学中出现过;之后是弹塑性理论涉及到的准则,包括屈服准则,用来定义材料何时从线弹性过渡到弹塑性;流动准则,用来确定塑性变形的方向;强化准则,用来给出塑性变形过程中屈服准则的强化规律。
2.1 应力-应变曲线
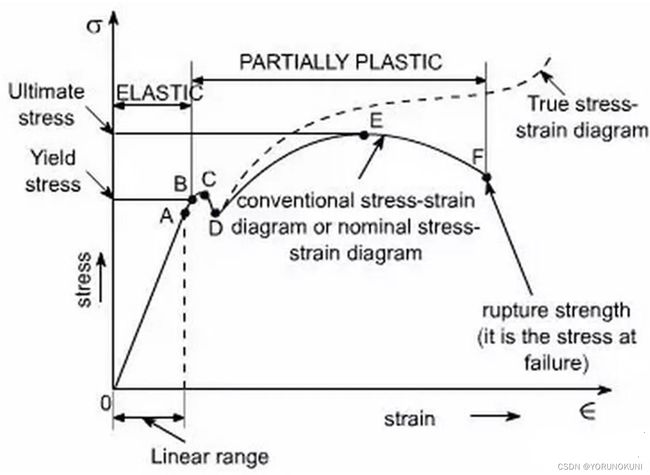
在材料力学中我们学过金属材料的单轴拉伸试验,单轴试验是最常见的材料试验,根据该试验我们可以得到材料的工程应力-应变曲线,如下图所示。通过该图对弹塑性分析中的一些概念进行介绍。
2.1.1 塑性与屈服极限
图中曲线OA段为材料的弹性阶段,应力-应变曲线处于线性正比关系,材料所产生的的变形均为弹性变形,卸载后可恢复原状。其中A点是弹性阶段的终点,该点的应力称为比例极限![]() 。当我们继续加载超过A点使曲线处于AB段时,材料的应力-应变关系就不再是线性了,即很小的应力增量就会产生很大的应变。如果继续加载超过B点,应力-应变曲线将进入塑性变形区域,此时卸去载荷后变形不能完全消除,材料出现永久的残余变形,这就是塑性变形。将B点的应力称为屈服极限
。当我们继续加载超过A点使曲线处于AB段时,材料的应力-应变关系就不再是线性了,即很小的应力增量就会产生很大的应变。如果继续加载超过B点,应力-应变曲线将进入塑性变形区域,此时卸去载荷后变形不能完全消除,材料出现永久的残余变形,这就是塑性变形。将B点的应力称为屈服极限![]() (或
(或![]() ),由于比例极限和屈服极限很接近,在ANSYS中假定两者相同,即OB段为弹性阶段,我们的线弹性分析均是在这一阶段进行的。
),由于比例极限和屈服极限很接近,在ANSYS中假定两者相同,即OB段为弹性阶段,我们的线弹性分析均是在这一阶段进行的。
还有一些材料也存在塑性变形,但是不会出现很明显的屈服阶段。对于这类材料,工程上规定把塑性应变达到0.2%时的应力值作为屈服极限。
2.1.2 工程曲线与真实曲线
图2.1中存在两条应力-应变曲线,其中实线称为工程应力-应变曲线,或名义应力-应变曲线,虚线称为真实应力-应变曲线。在ANSYS的材料非线性分析中我们使用的是真实应力-应变曲线,下面将对这两种曲线进行介绍。
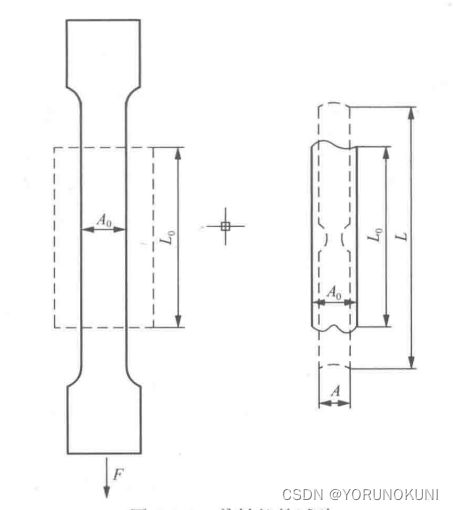
在单轴拉伸试验中,假定我们的试棒初始截面面积为![]() ,初始长度为
,初始长度为![]() ,变形后的截面面积为
,变形后的截面面积为![]() ,变形后的长度为
,变形后的长度为![]() ,载荷为F,如下图所示。
,载荷为F,如下图所示。
1. 工程应力-应变
计算公式如下所示,可以看出公式是基于小应变假设建立的,用结构的初始几何形状进行计算。但是在单轴拉伸试验中我们观察到,试棒的变形经历了4个阶段,即弹性阶段-屈服阶段-强化阶段-颈缩阶段,颈缩达到F点后发生断裂。
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
从公式中可以看出,在计算应力时并没有考虑到截面面积的变化,即使最后发生了颈缩,但工程应力的计算仍然使用了初始截面面积,这显然是不准确的。以E点的应力值为例,显然断裂时的截面面积减少了,所以真实的断裂应力应该大于工程断裂应力!在工程实践中,基于简单便于应用和安全的原理,可以继续使用工程应力-应变曲线,但是如果要模拟材料的非线性力学行为,还是要使用真实的应力-应变曲线。
2. 真实应力-应变
计算公式如下所示, 可以看出,在应力公式中使用了变形后的截面面积,应变也成了长度的非线性函数,显然更符合实际情况。
![]() (2.3)
(2.3)
假设在拉伸或压缩过程中材料体积不变,可以得到真实应力-应变和工程应力-应变之间的转换关系,公式如下:
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
在图2.1中可以看出,未到达屈服点前,真实应力应变与工程应力应变几乎完全吻合,因此若我们只进行线弹性分析,就不用对这两种曲线进行区分。但是过了屈服点之后两种曲线产生差别,真实应力要明显大于工程应力,因此当我们考虑塑性时就必须要使用真实应力-应变曲线了。
综上,在处理弹塑性材料时,我们的重点工作就是表示出屈服点后的应力-应变关系,这种关系可以通过线性拟合得到,并且根据拟合方法的不同,弹塑性材料的本构模型分成很多种类,这在下文会进行详述。
实例1:真实应力-应变的转换
已知工程应力和应变通过试验获得,且在200MPa时材料发生屈服,可以计算出线弹性阶段的弹性模量E=210GPa,真实应力可以通过式(2.6)计算获得,真实应变可以通过式(2.7)计算获得。我们得到的工程应变和真实应变都是总应变,其中包含了弹性应变和塑性应变,如式(2.8)所示。
![]() (2.8)
(2.8)
其中![]() 为弹性应变,
为弹性应变,![]() 为塑性应变。超过屈服点以后弹性变形就不再增加了,屈服点后的应变均为塑性应变。在定义材料过程中,有时我们需要知道材料的塑性应变,可通过下式获得:
为塑性应变。超过屈服点以后弹性变形就不再增加了,屈服点后的应变均为塑性应变。在定义材料过程中,有时我们需要知道材料的塑性应变,可通过下式获得:
![]() (2.9)
(2.9)
式中真实应变![]() 减去的项就是弹性应变
减去的项就是弹性应变![]() ,可通过真实应力和弹性模量计算得到。根据这些关系式我们可以轻松地完成下表。
,可通过真实应力和弹性模量计算得到。根据这些关系式我们可以轻松地完成下表。
| 工程应力(MPa) | 工程应变 | 真实应力(MPa) | 真实应变 | 塑性应变 |
|---|---|---|---|---|
| 200 | 0.00095 | 200.19 | 0.00095 | 0.0 |
| 240 | 0.025 | 246 | 0.0247 | 0.0235 |
| 280 | 0.05 | 294 | 0.0488 | 0.0474 |
| 340 | 0.1 | 374 | 0.0953 | 0.0935 |
| 380 | 0.15 | 437 | 0.14 | 0.138 |
| 400 | 0.2 | 480 | 0.182 | 0.18 |
3. 伸长率和断面收缩率
定义伸长率为:
![]() (2.10)
(2.10)
定义断面收缩率为:
![]() (2.11)
(2.11)
对于低碳钢:δ=20%~30%,ψ=50%~60%,这两个值越大说明材料塑性越好。工程上通常根据伸长率将材料分为两类:δ≥5%的为塑性材料,δ<5%的为脆性材料。
2.2 屈服准则
对于单向受拉的结构,通过对比轴向应力和屈服极限就可以判断出是否出现塑像变形,但是在工程中遇到的结构往往会受到拉压、扭转、弯曲、剪切等多种载荷的作用,从而产生多轴应力。在多轴状态下要如何判断结构是否屈服呢?根据屈服准则可以将多轴应力转换成一个标量,即等效应力,将等效应力与单轴屈服极限对比。简而言之,屈服准则用于定义材料在何时从线弹性转变为弹塑性。
ANSYS中设置多种屈服准则,如Von Mises屈服准则,Hill屈服准则,广义Hill屈服准则,下面我们将逐一介绍。
2.2.1 Von Mises屈服准则
这是一个比较通用的准则,尤其适用于各向同性的金属材料,该屈服准则的等效应力计算公式如下:
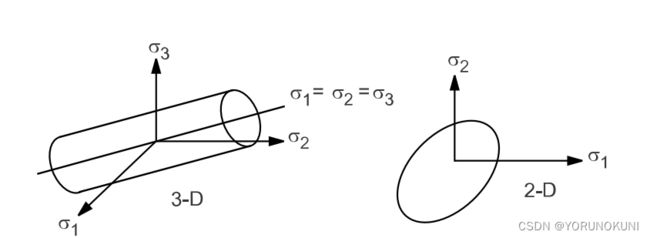
三维坐标系下的函数图像如下所示,可以看出屈服面是一个以![]() 为中心线的圆柱面,在2D空间(σ3=0)下屈服面是一个椭圆,长轴在45°方向上。在屈服面内的任何应力状态都是弹性的,相反屈服面外的应力状态会造成屈服。但是该屈服准则没有考虑静水压力(三个主应力相等时)对屈服的影响,即处于静水压力下不会屈服,根据式(2.12)算出的等效应力为0。其实金属材料在工程中几乎不会遇到三个主应力相等的情况。
为中心线的圆柱面,在2D空间(σ3=0)下屈服面是一个椭圆,长轴在45°方向上。在屈服面内的任何应力状态都是弹性的,相反屈服面外的应力状态会造成屈服。但是该屈服准则没有考虑静水压力(三个主应力相等时)对屈服的影响,即处于静水压力下不会屈服,根据式(2.12)算出的等效应力为0。其实金属材料在工程中几乎不会遇到三个主应力相等的情况。
2.2.2 Hill屈服准则
相对于Von Mises屈服准则,Hill准则可以考虑金属材料的弹性参数的各向异性和屈服强度的各向异性,等效应力的计算公式如下:
(2.13)
其中6个材料常数H、F、G、N、L、M可以通过试验结果获得,计算公式如下:
(2.14)
上式右端的6个常数为材料的屈服应力比率,计算公式如下:
(2.15)
其中![]() 为各个方向的屈服应力,
为各个方向的屈服应力,![]() 为参考屈服应力。Hill准则的屈服面与Mises准则的屈服面相同。
为参考屈服应力。Hill准则的屈服面与Mises准则的屈服面相同。
2.2.3 广义Hill准则
该准则是对Hill准则的进一步延伸,不仅考虑了材料在三个正交方向上屈服强度的不同,而且还考虑了拉伸状态和压缩状态下屈服强度的不同。等效应力的计算公式如下:
(2.17)
上式中,![]() 和
和![]() 分别是j方向的拉伸和压缩屈服强度,将压缩屈服应力视为正值处理。单轴屈服强度值的选取需要使得以下两个等式成立:
分别是j方向的拉伸和压缩屈服强度,将压缩屈服应力视为正值处理。单轴屈服强度值的选取需要使得以下两个等式成立:
(2.18)
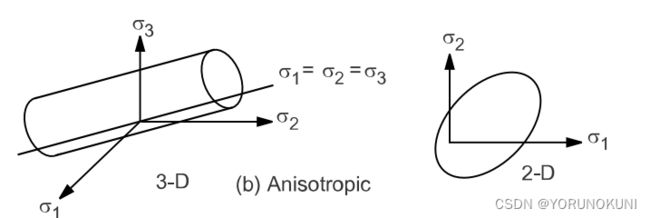
广义Hill准则的屈服面如下图所示。
2.3 流动准则
流动准则定义了发生屈服时塑性应变的方向,由下面的方程给出:
![]() (2.19)
(2.19)
其中λ为塑性乘子,决定了塑性应变量,Q为塑性势,决定了塑性应变的方向。流动准则可以分为关联流动和非关联流动:
- 关联流动:Q是屈服函数,塑性应变垂直于屈服面,塑性流动方向与屈服面法线方向相同。适用于金属和其他呈现不可压缩的非弹性材料。
- 非关联流动:塑性应变不垂直与屈服面,适用于内部摩擦滑动而塑性变形的土壤和颗粒材料,如ANSYS APDL中的Drucker-Prager本构模型,该模型在Workbench中没有集成,需要通过命令进行添加,在后面遇到时会详细描述。
2.4 强化准则
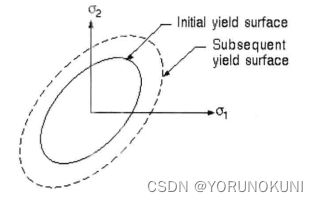
强化准则描述了初始屈服准则随着塑性应变的增加是如何发展的。对于理想弹塑性材料,屈服面保持不变。但是实际工程上,当材料应力超过屈服面后,卸载后重新加载,后继屈服面的这个圆柱形状的轴心、尺寸、形状等都有可能发生改变,强化准则的作用便是描述屈服面的变化,确定材料在重新加载时的屈服点。例如,机加工中的喷丸处理,零件经过喷丸后表面的屈服应力相较于未处理时会提高,零件表面得到强化。在ANSYS中使用了三种强化准则,如下所示:
1. 等向强化:也称为各项同性硬化,是指屈服面在所有方向上均匀扩张。由于等向强化,所以在受压方向的屈服应力等于受拉过程中达到的最大应力值。
例如,经单轴拉伸试验获得一个金属试棒的拉伸屈服应力为200MPa,认为试棒的拉伸屈服应力和压缩屈服应力相同。在等向强化的规则下,拉伸试棒使结构的最大应力到250MPa,显然此时已经出现了塑性变形;之后卸去载荷,对试棒反向施加压力,可以观察到,在压力的作用下试棒的压缩屈服强度变为了250MPa,这就是等向强化。
等向强化一般用于大应变或单向屈服加载的计算中,不适用于交变载荷!
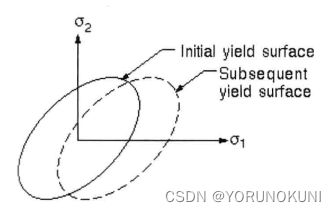
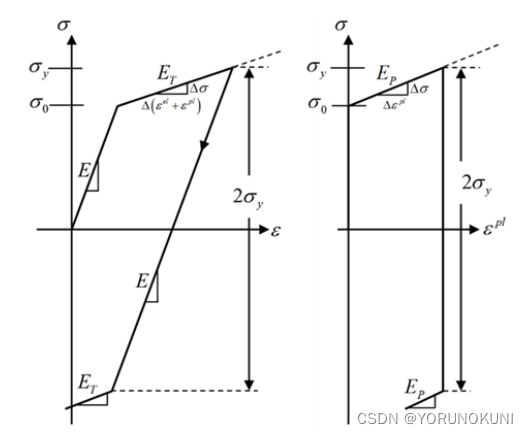
2. 随动强化:屈服面的大小保持不变,仅在屈服方向移动,适用于对于大多数小应变交变载荷的金属材料。随动强化满足包辛格效应,即当某个方向的屈服应力升高时,相反方向的屈服应力下降,且两个屈服应力保持2![]() 的关系。
的关系。
例如,还是上一个拉伸屈服应力![]() 为200MPa的金属试棒,拉伸屈服应力加上压缩屈服应力为400MPa。当试棒在拉力作用下使拉伸屈服应力变为250MPa时,根据包辛格效应,此时的压缩屈服应力应该为150MPa。
为200MPa的金属试棒,拉伸屈服应力加上压缩屈服应力为400MPa。当试棒在拉力作用下使拉伸屈服应力变为250MPa时,根据包辛格效应,此时的压缩屈服应力应该为150MPa。
要注意,在发生屈服以后,由于产生随动强化,各向同性材料不再保持各向同性。 对于大应变仿真,由于包辛格效应,材料的压缩屈服强度可能移动到0线以上,明显不合实际,这种情况将在下文进行描述。
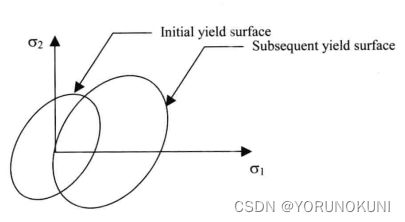
3. 混合强化:即等向强化和随动强化的结合,屈服面既在大小上扩张,也在屈服的方向上移动。等向强化与随动强化是两个极端,真实的材料往往是介于两者之间的混合强化。
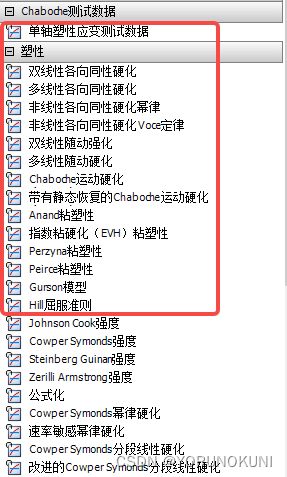
3. 常用弹塑性本构模型
Workbench的材料库中提供了多种塑性本构模型,同时Chaboche也支持用户自己定义塑性应变的试验数据,具体塑性模型如下图所示,红框外的模型用于显示动力学分析,在本文不过多介绍。
3.1 Chaboche测试数据
通过Chaboche测试数据可以添加单轴塑形应力应变的测试数据,输入数据为塑形应变与真实应力,适用于大应变和循环载荷。将塑性应变和应力值输入表格,可以得到塑性应变曲线。相关数据可以在附件中下载。
3.2 线性强化
上文提到过,在处理弹塑性材料时,我们的工作重点就是拟合出屈服后的应力-应变关系,并且根据拟合方法的不同,弹塑性材料的本构模型分成很多种类。线性强化模型就是使用线性关系拟合屈服后的应力-应变曲线,如果用一条线拟合,就称为双线性,如果使用多条线拟合,就成为多线性。Workbench中的线性强化本构模型有双线性等向强化、多线性等向强化、双线性随动强化和多线性随动强化,下面将依次介绍。
3.2.1 双线性等向强化
双线性等向强化使用两根线性线段描述材料的整个应力-应变关系,第一根直线的斜率E即为材料的弹性模量,第二根线段用来表示屈服后的应力-应变关系,这条线的斜率应该大于0且小于E,第二根线段的斜率有两种定义方式,如下图所示。
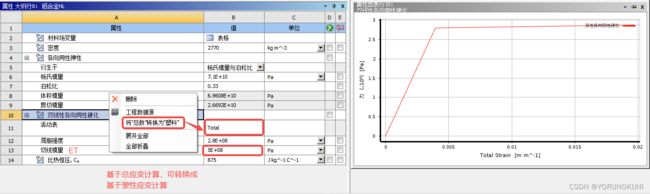
利用总应变计算![]() :已知屈服点的坐标为(
:已知屈服点的坐标为(![]() ),塑性变形阶段一点的坐标为(
),塑性变形阶段一点的坐标为(![]() ),计算公式如下:
),计算公式如下:
![]() (3.1)
(3.1)
利用塑性应变计算![]() :已知屈服点的坐标为(
:已知屈服点的坐标为(![]() ),初始位置塑性变形为0,所以该线段描述的是塑性变形和应力的关系,另一点坐标为(
),初始位置塑性变形为0,所以该线段描述的是塑性变形和应力的关系,另一点坐标为(![]() ),计算公式如下:
),计算公式如下:
![]() (3.2)
(3.2)
同时,这个两个斜率满足下式关系:
![]() (3.3)
(3.3)
在Workbench中的设置界面如下:
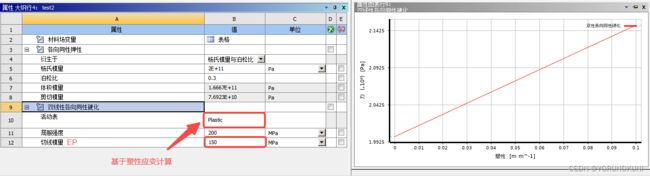
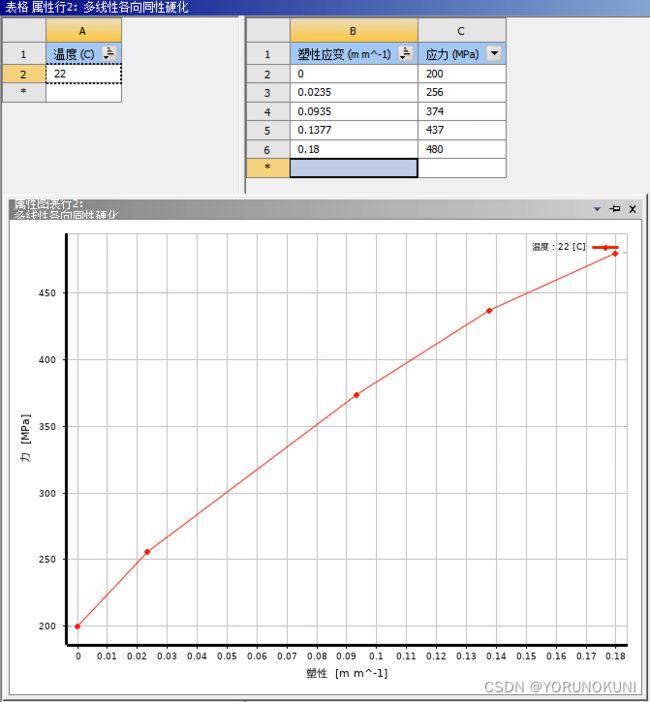
3.2.2 多线性等向强化
多线性与双线性的区别在于,多线性是用多条线段来定义应力-应变曲线的。其中,每两个点之间都是线性关系,第一个点对应的应力值是材料的屈服应力,如下图所示。
在Workbench中通过输入多个点的塑性应变和应力值来定义多线性模型,即通过相邻两个点都可以计算出一个Ep。
3.2.3 双线性/多线性随动强化
双线性和多线性随动强化的设置与双线性和多线性等向强化完全相同,区别仅在于随动强化模型可以模拟材料在单轴和循环载荷下的响应,同时可用于模拟包辛格效应。一般用于小应变(应变≤5%~10%)和双向屈服循环加载的计算中。
3.3 非线性强化
非线性强化本构模型顾名思义就是用非线性函数去拟合材料的塑性段曲线,分为非线性等向强化和非线性随动强化,下面将对这两种本构模型的非线性拟合方法进行叙述。
3.3.1 非线性等向强化
非线性等向强化分为Power模型和Voce模型,这是两种不同的拟合方法。
1. Power模型:基于Power函数的非线性等向强化需要定义2个参数,初始的屈服应力![]() 和指数系数N,计算公式如下:
和指数系数N,计算公式如下:
其中,![]() 为当前的屈服应力,G为剪切模量,
为当前的屈服应力,G为剪切模量,![]() 为累积塑性应变,是塑性应变
为累积塑性应变,是塑性应变![]() 的函数,0≤N<1。当N=0时,应力-应变曲线为理想弹塑性模型,N越大曲线越陡峭。在Workbench中的设置界面如下:
的函数,0≤N<1。当N=0时,应力-应变曲线为理想弹塑性模型,N越大曲线越陡峭。在Workbench中的设置界面如下:
2. Voce模型:该模型类似于双线性等向强化,只是在线性项上添加了指数饱和强化项,计算公式和曲线图如下。
其中,需要定义的参数有4个,分别是![]() 初始屈服应力,
初始屈服应力,![]() 线性系数,
线性系数,![]() 指数系数,b指数饱和参数。 这个材料模型适用于大应变分析,下面介绍这几个参数如何获取。
指数系数,b指数饱和参数。 这个材料模型适用于大应变分析,下面介绍这几个参数如何获取。
![]() :从图中可以看出,这个参数是大应变段的斜率。因此,将试验得到的应力-塑性应变曲线分为两端,第二段为曲率近似不变的大应变段。在该段取两个点,直接计算出斜率
:从图中可以看出,这个参数是大应变段的斜率。因此,将试验得到的应力-塑性应变曲线分为两端,第二段为曲率近似不变的大应变段。在该段取两个点,直接计算出斜率![]() ;
;
![]() :从图中可以看出,将大应变段的线段延伸至交于纵轴,交点处的应力值为
:从图中可以看出,将大应变段的线段延伸至交于纵轴,交点处的应力值为![]() +
+![]() 。因此,计算出
。因此,计算出![]() 后可以得到相应的直线公式,进一步就可以计算出直线与纵轴的交点了,之后用交点值减去已知的初始屈服应力
后可以得到相应的直线公式,进一步就可以计算出直线与纵轴的交点了,之后用交点值减去已知的初始屈服应力![]() ,就可以得到
,就可以得到![]() ;
;
b:b和![]() 的乘积为塑性应变刚开始时的初始斜率,得到这个斜率后即可计算出b;
的乘积为塑性应变刚开始时的初始斜率,得到这个斜率后即可计算出b;
从公式可以看出,当b=0时,该模型就变成了双线性等向强化模型;在Workbench中的设置界面如下图:
3.3.2 非线性随动强化(Chaboche)
Chaboche随动强化可模拟包辛格效应,而且适用于大应变和循环加载,可用于模拟循环硬化或软化,以及棘轮或调整行为,该强化模型支持最多5中随动强化模型的背应力进行叠加。
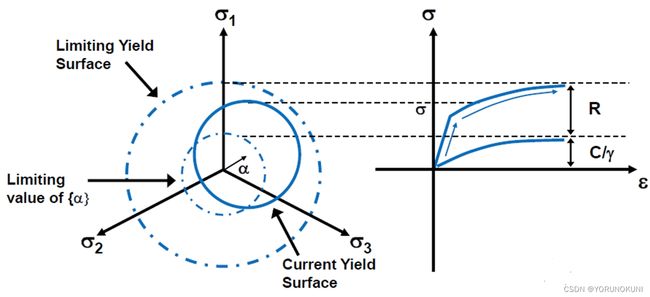
背应力即强化后的屈服面中心相对于初始屈服面中心的矢量α,在上文强化内容中讲过,等向强化时屈服面均匀扩张,但中心不变,随动强化时屈服面不变,但中心出现移动。Chaboche随动强化就是将多个独立的随动强化叠加在一起,计算公式如下:
![]() (3.6)
(3.6)
α为总的背应力,第i个背应力的计算如下:
总应力计算公式如下:
![]() (3.8)
(3.8)
其中![]() 为初始屈服应力,n为随动强化的个数,在Workbench中取值为1到5,
为初始屈服应力,n为随动强化的个数,在Workbench中取值为1到5,![]() 和
和![]() 为材料参数。从公式中可以看出,当
为材料参数。从公式中可以看出,当![]() 且
且![]() 时,Cho模型即为双线性随动强化模型。同时,从图中可以看出,屈服面存在一个界限,接近这个界限时材料会出现理想弹塑性的特征。Chaboche模型也可以与等向强化模型结合使用,组成混合强化模型。在Workbench中的设置界面如下所示,这些参数均可以通过软件拟合获得。
时,Cho模型即为双线性随动强化模型。同时,从图中可以看出,屈服面存在一个界限,接近这个界限时材料会出现理想弹塑性的特征。Chaboche模型也可以与等向强化模型结合使用,组成混合强化模型。在Workbench中的设置界面如下所示,这些参数均可以通过软件拟合获得。
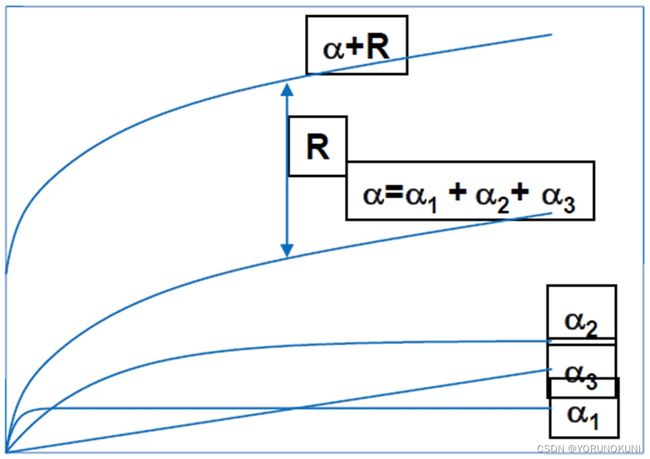 图3.12 Chaboche随动强化模型
图3.12 Chaboche随动强化模型 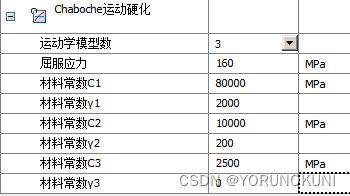 图3.13 Chaboche模型的设置界面
图3.13 Chaboche模型的设置界面
3.4 Hill准则及其余材料模型
3.4.1 Hill准则的设置
在上文讲过,Hill准则时对Mises准则的扩张,适用于各向异性材料。当材料中未设置Hill准则时,默认使用Mises准则,如果设置了Hill准则,则程序使用Hill准则。Workbench中的设置界面如下:
默认情况下表示不考虑蠕变,用户只需要设置材料6个方向的屈服应力比率![]() 。当所有的
。当所有的![]() 都等于1时,Hill准则就变为了Mises准则。
都等于1时,Hill准则就变为了Mises准则。
3.4.2 其余材料模型
在图3.1中可以看到,Workbench的塑性模型中还有一些粘塑性本构,如Anand模型,EVH模型等等,粘塑性类似于蠕变,是率相关塑性,且材料本构要求温度必须大于熔点的一半,没有明显的屈服点,也没有加载与卸载准则,常用于模拟材料的高温塑性加工和电子器件的钎焊接头。这部分内容下后面的文章中会进行详细介绍。Gurson模型用来分析延性多孔金属的塑性和损伤,如果用到的话会在其他文章进行介绍。
4. 循环加载
试验中载荷的施加方式可以分为单调加载和循环加载:
- 单调加载是指没有卸载过程,试验得到的单调应力-应变曲线适用于长期承载作用的结构;
- 循环加载可以分为对称加载和非对称加载,在对称加载中,对于屈服比≤0.7的材料会发生循环强化,如退火、正火材料;屈服比≥0.8的材料会发生循环软化,如淬火、调质材料;屈服比介于0.7和0.8之间的材料现象不明显。在非对称加载情况下,材料会发生棘轮或调整现象。这些情况在本节会进行详细介绍。
4.1 循环强化和软化
4.1.1 循环强化
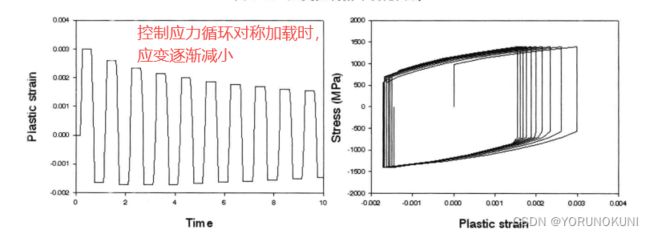
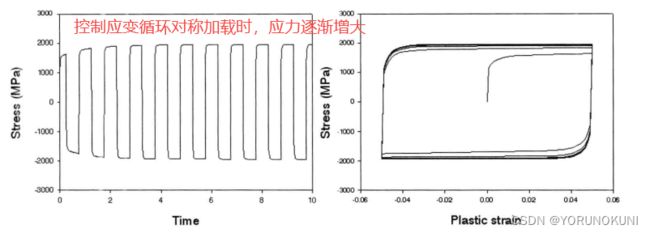
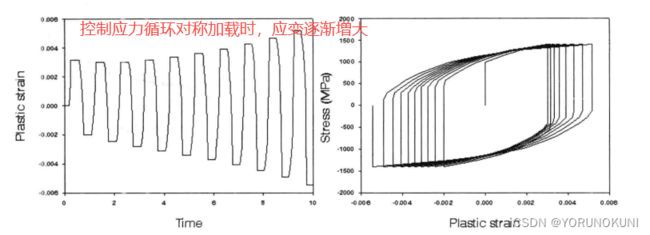
循环强化:在低周疲劳试验中,使用循环加载且保证循环载荷的绝对值相等,当控制应力加载时,会发现应变随循环的增加而减小;或者控制应变循环时,会发现应力随循环的增加而变大;简而言之,在力加载时,即使我们使用的载荷不变,但是随着循环次数的增加,相同载荷产生的应变反而减小了,即结构在循环加载过程中逐渐变硬。
Chaboche加上任何等向强化准则(双线性, 多线性, 非线性)用于模拟循环强化,等向强化准则将增大具有循环应变的屈服应力 。
4.1.2 循环软化
循环软化:与循环强化相反,即结构随着载荷的循环逐渐变软。
Chaboche模型加上Voce非线性等向强化模型 (NLISO) 用于模拟循环软化。
一般情况下,低强度、软材料趋向于循环强化,高强度、硬材料趋向于循环软化。
4.2 棘轮和调整现象
棘轮和调整现象均发生在非对称循环加载中,两者的区别在于塑性变形的发展趋势。
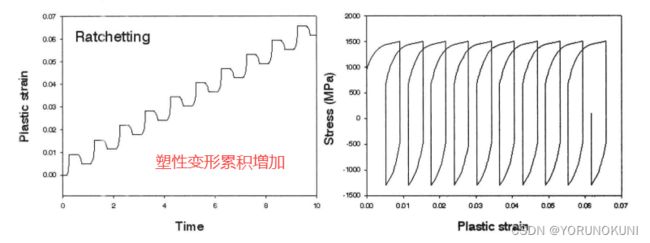
4.2.1 棘轮
棘轮:在非对称循环应力作用下,材料的塑性应变在每一个循环中累计增加,当棘轮变形达到等量循环增加、加速增加的畸变状态或循环饱和状态时,塑性累积导致尺寸超标或循环破坏失效。主要用于压力容器、高压管道、轨道接触和电子封装。
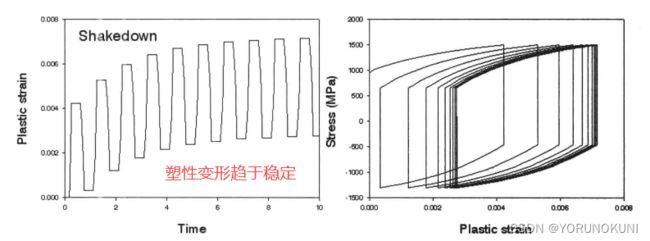
4.2.2 调整
调整:在非对称循环应力作用下,材料的塑性应变在每一个循环中趋于稳定。不同于棘轮的塑性应变累积增加,在到达一定程度后保持不变。
要注意,线性随动强化模型是不能描述棘轮和调整现象的,需要使用非线性随动强化。
Chaboche模型中,当![]() 且所有时
且所有时![]() ,可以模拟棘轮;
,可以模拟棘轮;
Chaboche模型中,当![]() 且有1~(n-1)个
且有1~(n-1)个![]() 时,可以模拟调整;
时,可以模拟调整;
5. 注意事项
5.1 输出量的变化
在有限元分析中,总应变![]() 是由多个部分组成的,如下式所示:
是由多个部分组成的,如下式所示:
(5.1)
其中![]() 为弹性应变,
为弹性应变,![]() 为塑性应变,
为塑性应变,![]() 为蠕变应变,
为蠕变应变,![]() 为热应变,
为热应变,![]() 为膨胀应变,如果只做包含材料非线性的静力分析,那么总应变应该只包含弹性应变和塑性应变,如下式。
为膨胀应变,如果只做包含材料非线性的静力分析,那么总应变应该只包含弹性应变和塑性应变,如下式。
![]() (5.2)
(5.2)
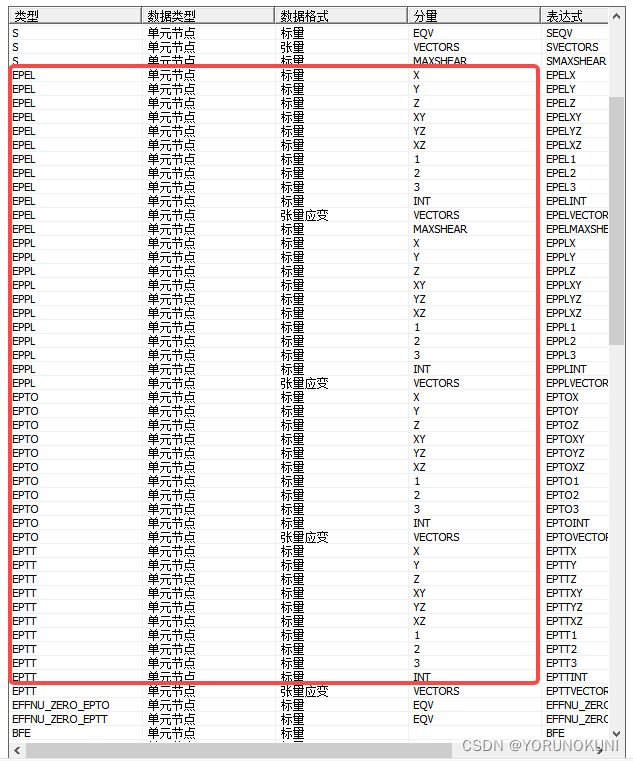
在Workbench中查看后处理可输出的物理量,红框部分就是可输出的应变量,包括弹性应变、塑性应变、总机械应变EPTO(不含热应变)和总应变EPTT(含热应变)。如果分析中没有温度场,那么总机械应变和总应变的值相等。
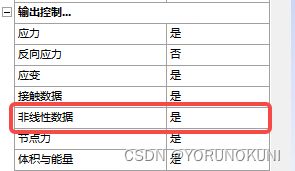
Workbench的后处理可以显示塑性材料计算过程中的一些结果,但这些非线性输出需要我们手动设置,设置界面如下图,需要在“输出控制”中将“非线性数据”打开,在后处理中会出现一些前标为NL的物理量。简单介绍一些这些输出量,NLEPEQ—累积等效塑性应变,NLHPRE—静水压应力(这个物理量在下一章超弹性材料分析中,判断是否出现体积自锁时会用到),其他参数的含义可以参考下面的文章。
《ANSYS常用术语(命令)中英文对照_tophy_新浪博客 (sina.com.cn)》
需要注意,塑性输出量实际上是指距离节点最近的那个积分点上的值,而不是通过积分点外推得到的,这与线弹性分析不同。
5.2 塑性分析的基本原则
下面这些原则有助于塑性分析更加准确:
- 缓慢加载,控制步长保证在一个时间步内,最大塑性应变增量不超过5%;
- 控制结构和网格,保证不出现应力奇异;
- 可以使用线搜索来加强收敛;
- 在小位移和小应变塑性分析中可以使用修正牛顿法或初始刚度;