Manacher算法详解

 

1 Manacher算法解决的问题

 

求解字符串str中 最长回文子串的长度

比如 字符串 readlemonnomelwrite 最长回文长度为 10

---

 

2 暴力解法

 

求字符串 abcfff 的最大回文长度

从0开始到N - 1遍历字符串,每到一个位置 已该位置为中心,向左右两边扩,直到找到最长的回文子串

a b c f f f

 

假设回文子串的长度为偶数,则使用这种方法找不到 比如 :

a b b a f f f

因此我们在目标字符串第一个字符之前,所有字符之后加入一个特殊字符

#a#b#b#a#f#f#f#

并不要求连接的字符串是原串中出现的字符

暴力解法的时间复杂度 :  $O(n^2)$

---

 

3 算法相关的概念

 

1) 回文直径
 

以一个字符为中心,扩出来的区域的大小

比如字符:
#1#2#3#a#b#a#0#i#k

以字符 b为中心的回文直径为 7

 

2) 回文半径
 

回文直径一半的长度,上述字符的的回文半径为 $4$

 

3) 最右回文右边界
 

每次扩的时候,字符串str 的右边界变大了,则更新 最右边界的长度

以字符 #1#2#3#a#b#a#0#i#k为例

初始 : int R = -1

第一个字符 R = 0

第二个字符最长回文子串为 #1# R = 3

……

到了b字符时最长回文子串 #a#b#a# 7 R = 12

 
4) 中心点C
 

到最右回文边界时,中心点的位置

---

 

4 几种情况分析

 
i为当前来到的位置

1. i 位置在最右回文边界外
   

   此种情况下直接暴力扩

2. i 位置在最右边界的 R 内部
   

R 之前配出来的最大回文子串的右边界

1. 细分情况1
   i' 为中心的回文字符串在 L ~ R 范围内
   

i 的回文和 i'位置的回文字符串一样. i位置就不需要扩

接下来证明 :

由对称关系可以得出
s1段的字符和 s2段的字符一一对应相等
s2段的字符和 s3段的字符一一对应相等
s3段的字符和 s4段的字符一一对应相等
s1段的字符和 s4段的字符一一对应相等

可以推出 s3段的字符和 s4段的字符是一一对应相等的

i位置的回文直接会不会更长呢?
假设s1段的前一个位置的字符是 m
s2段后面的一个字符是 n
s3段的前一个字符是 p
s4段的后一个字符是q

由图可以看出
m != n
m == q
n == p
所以 q != p

因此i位置的回文直径就是 i'的回文直径

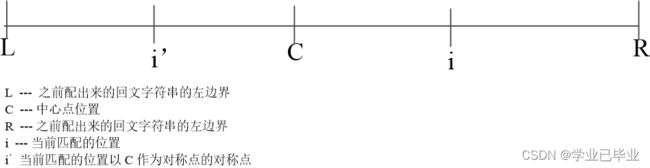
i'位置的求法 :
C R 已知

$i=C+(R-C)/2$
$C=L+(R-L)/2$
$i^{\prime }=L+(C-L)/2$

$2i=C+R$
$R=2i-C$
$C=2i-R$
$2C=L+R$
$L=2C-R$

$2i^{\prime }=L+C$
$2i^{\prime }=2C-R+2i-R=2C-2R+2i$
$i^{\prime }=C-R+i=C-(2i-C)+i=2C-i$

2. 细分情况2
   i' 为中心的回文字符串在 L ~ R 范围外,则此时i的回文半径为 i ~ R

L' —   L 以 i' 为对称点的对称点
R' —   R以i为对称点的对称点
m —   L的前一个字符串
p —   L'后一个字符串
p —   R'的前一个字符串
n —   R的后后一个字符串

由对称关系可以得出
m == p
p==q

因为 m,n在 L ~ R范围外,因此m != n,进而可以推出 q != n
因此此种情况下,i位置的回文半径为 R - i + 1

3. 细分情况3
   i'的回文半径压到L边界上
   
   在此种情况下,i位置的回文子串需要继续往两边扩,方可找到最大的回文半径

Manacher算法时间复杂度估计 $O(n)$

---

 

5 代码实现

 

/**
  * 给字符str加上特殊字符串
  * @param str
  * @return
  */
 public static char[] manacherString(String str){
     char[] chars = str.toCharArray();
     char[] retCharArr = new char[chars.length << 1 + 1];
     int index = 0;
     for (int i = 0; i < retCharArr.length;++i){
     	  //偶数位置处的字符为特殊字符
         retCharArr[i] = (i & 1) == 0 ? '#' : chars[index++];
     }
     return  retCharArr;
 }

 /**
  * 求最大回文子串
  * @param str
  * @return
  */
 public static int maxLcpsLenth(String str){
     if (str == null || str.length() == 0){
         return 0;
     }
     char[] s = manacherString(str);
     int[] pArr = new int[s.length];//回文半径数组

     int C = -1;//中心点
     int R = -1;// 回文右边界再往右一个位置  最右的有效区域是 R - 1位置
     int max = Integer.MIN_VALUE;// 扩出来的最大值

     // 每一个位置都求回文半径
     for (int i = 0; i < s.length;++i){
         /**
          * 不需要验证的区域
          * 1) i位置在 R 的外部 则不需要验证的长度为 1
          * 2) i 位置在 R 内部
          *      i' 为中心的回文字符串在 L ~ R 范围内 pArr[i'] 此时 pArr[i'] < R - i
          *      i' 的回文半径压到 L 边界上 R - i
          *      i' 为中心的回文字符串在L ~ R范围外 R - i
          * */
         pArr[i] = R > i ? Math.min(pArr[2 * C - i],R - i) : 1;

         // 往外扩 在扩的过程中 左边不能越界 右边也不能越界
         while ( i + pArr[i] < s.length && i - pArr[i] > -1){
             // 可以往往外扩
             if (s[i + pArr[i]] == s[i - pArr[i]]){
                 pArr[i]++;
             } else {
                 break;
             }
         }
         // 最右侧的位置
         if(i + pArr[i] > R){
             R = i + pArr[i];
             C = i;
         }
         max = Math.max(max,pArr[i]);
     }
     return max - 1;
 }

 
leetcode 代码

import java.util.*;


public class Solution {
  // 在字符串str的每个字符前面 及最后一个字符的后面加入特殊字符 #
  public char[] manacherString(String str) {
    char[] chars = str.toCharArray();
    char[] retCharArr = new char[(chars.length << 1) + 1];

    int index = 0;
    for (int i = 0; i < retCharArr.length; ++i) {
      retCharArr[i] = ((i & 1) == 0 ) ? '#' : chars[index++];
    }
    return retCharArr;
  }


  /**
   * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
   *
   *
   * @param A string字符串
   * @return int整型
   */
  public int getLongestPalindrome (String A) {
    // write code here
    if (A == null || A.length() == 0) {
      return 0;
    }
    int max = Integer.MIN_VALUE;

    char[] str = manacherString(A);
    // 回文半径数组
    int[] pArr = new int[str.length];
    // 回文字符串匹配的最右边界
    int R = -1;
    // 半径
    int C = -1;
    for (int i = 0; i < str.length; ++i) {
      // 不需要计算就匹配的路径
      pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;
      // 求 i位置的回文
      while ((i + pArr[i]) < str.length && (i - pArr[i]) > -1) {
        if (str[(i + pArr[i])] == str[(i - pArr[i])]) {
          ++pArr[i];
        } else {
          break;
        }
      }
      // 更新 R
      if (i + pArr[i] > R) {
        R = i + pArr[i];
        C = i;
      }
      max = Math.max(max, pArr[i]);
    }
    return max - 1;
  }
}