10.6数构(概念,优先队列复习,漏斗倒水时间期望,小木棍dfs,括号匹配,后缀表达式,PTA第三题)
选择应试
数据项是数据的最小单位
数据的逻辑结构与数据元素本身的内容和形式无关
带头结点的单循环链表中,任一结点的后继结点的指针域均不空
顺序存储结构的主要缺点是不利于插入或删除操作
顺序存储方式不仅能用于存储线性结构,还可以用来存放非线性结构,例如完全二叉树是属于非线性结构,但其最佳存储方式是顺序存储方式
如果元素个数已知,且插入删除较少的可以使用顺序结构,而对于频繁有插入删除操作,元素个数未知的,最好使用链式结构,
在线性表的顺序存储结构中,插入和删除元素时,移动元素的个数与该元素的位置有关
在具有头结点的链式存储结构中,头指针并非指向链表中的第一个元素结点,头指针指向的是头结点
链式存储的优点是插入、删除元素时不会引起后续元素的移动,缺点是只能顺序访问各元素
循环链表可以做到从任一结点出发,访问到链表的全部结点
在顺序表中逻辑上相邻的元素,其对应的物理位置也是相邻的
链表中的每个结点可含多个指针域,分别存放多个指针。例如双向链表中的结点可以含有两个指针域,分别存放指向其直接前趋和直接后继的指针
环形队列中有多少个元素可以根据队首指针和队尾指针的值来计算
n个元素进队的顺序和出队的顺序总是一致的
栈和队列的存储方式,既可以是顺序方式,也可以是链式方式
对顺序栈进行进栈、出栈操作不涉及元素的前、后移动问题
循环队列也存在着空间溢出问题。
-
循环队列执行出队操作时会引起大量元素的移动。F
解析:出队对队首指针进行操作就行。
-
在用数组表示的循环队列中,front值一定小于等于rear值。F
解析:环形循环队列font的值有可能大于rear。
-
在n个元素连续进栈以后,它们的出栈顺序和进栈顺序一定正好相反。T
-
对于一个有N个结点、K条边的森林,不能确定它共有几棵树。F
解析:设边的数目 EdgeNum, 树的数目为 TreeNum
根据 NodeNum - 1 = EdgeNum(对每棵树而言)
所以 (NodeNum1 - 1) + … + (NodeNumi - 1) = K
即 N - TreeNum = K`
在循环顺序队列中,假设以少用一个存储单元的方法来区分队列判满和判空的条件,front和rear分别为队首和队尾指针,它们分别指向队首元素和队尾元素的下一个存储单元,队列的最大存储容量为maxSize,则队列的长度是(rear-front+maxSize)%maxSize
在少用一个元素空间的循环队列(m为最大队列长度)是满队列的条件(B )。
A.rear==front B.(rear+1)%m==front
C.(rear+1)==front D.front==(front+1)%m
循环队列队空条件:Q.front==Q.rear
循环队列队满条件:(Q.rear+1)%MAXQSIZE==Q.front
设固定容量的循环队列中数组的下标是0~N-1,其队头队尾指针分别为f和r(f指向队首元素的前一位置,r指向队尾元素),则其元素个数为___D___。
A. r-f
B. r-f-1
C. (r-f)%N+1
D. (r-f+N)%N
应当注意的是,循环队列中,应保持队头,队尾指针有其中之一是虚指,即不能都是实指
由两个栈共享一个数组空间的好处是节省存储空间,降低上溢出发生的机率
循环队列不会产生假溢出
若某循环队列有队首指针front和队尾指针rear,在队不空时出队操作仅会改变front
入队改变rear
漏斗倒满水的充满时间期望
const int N = 1e6;
struct node {
double data;
double sum;
double wait;
double ex;
int pre;
vectorchild;
}list[N];
void link(int x, int y) {
list[x].child.push_back(y);
}
int n;
double sum1;
void fuzhi(int i) {
sum1 = 0;
int len = list[i].child.size();
for (int j = 0; j < len; j++) {
sum1 += list[list[i].child[j]].sum;//得到这一层的所有权和
}
for (int j = 0; j < len; j++) {
list[list[i].child[j]].wait = (sum1 - list[list[i].child[j]].sum) / 2.0 + list[i].wait;//减掉自己的权和就是剩下的权和
list[list[i].child[j]].ex = list[list[i].child[j]].wait + list[list[i].child[j]].sum;
}
// cout << list[i].sum << " " << list[i].wait << " " << " " << list[i].ex << endl;
}
cin >> n;
list[1].pre = 0;
for (int i = 1; i <= n; i++) {
cin >> list[i].data;
list[i].sum = list[i].data;
}
for (int i = 1; i <= n - 1; i++) {
int f, b;
cin >> f >> b;
list[b].pre = f;
link(f, b);
}
for (int i = 1; i <= n; i++) {
int p = list[i].pre;
while (p != 0) {
list[p].sum += list[i].data;
p = list[p].pre;
}
}
//cout << list[1].sum << " " << list[1].wait << " " << " " << list[1].ex << endl;
list[1].ex = list[1].sum;
queueq;
q.push(1);
while (!q.empty()) {
int cur = q.front();
q.pop();
fuzhi(cur);
int len = list[cur].child.size();
for (int i = 0; i < len; i++) {
q.push(list[cur].child[i]);
}
}
for (int i = 1; i <= n; i++) {
//cout <<"编号 " << i << " 前驱结点 " << list[i].pre << " " << list[i].sum << "+" << list[i].wait << "=" << list[i].ex << endl;
// printf("%.2lf ", list[i].ex);
cout << fixed << setprecision(2) << list[i].ex << " ";
} 改错
1.括号匹配,
考虑左括号多,右括号少,而且左括号一直是符合条件的情况
所以最后一定是要判断栈是否为空的,而且是在flag成立的基础上
可以尝试只保留唯一正确时的输出判定if条件,其他都是错的
string s;
int n;
cin >> n;
while (n--) {
cin >> s;
stackst;
bool flag = true;
for (int i = 0; i < s.size(); i++) {
if (s[i] == '{') {
if (st.empty()) {
st.push('}');
}
else if (st.top() == '}') {
st.push('}');
}
else {
flag = false;
cout << "NO" << endl;
break;
}
}
else if (s[i] == '[') {
if (st.empty()) {
st.push(']');
}
else if (st.top() == '}' || st.top() == ']') {
st.push(']');
}
else {
flag = false;
cout << "NO" << endl;
break;
}
}
else if (s[i] == '(') {
if (st.empty()) {
st.push(')');
}
else if (st.top() == '}' || st.top() == ']' || st.top() == ')') {
st.push(')');
}
else {
flag = false;
cout << "NO" << endl;
break;
}
}
else if (s[i] == '<') {
if (st.empty()) {
st.push('>');
}
else if (st.top() == '}' || st.top() == ']' || st.top() == ')' || st.top() == '>') {
st.push('>');
}
else {
flag = false;
cout << "NO" << endl;
break;
}
}
if (st.empty()) {
flag = false;
cout << "NO" << endl;
break;
}
else if (s[i] != '{' && s[i] != '[' && s[i] != '(' && s[i] != '<') {
if (s[i] == st.top()) {
st.pop();
}
else {
flag = false;
cout << "NO" << endl;
break;
}
}
}
if (flag&&st.empty()) {
cout << "YES" << endl;
}
else {
cout << "NO" << endl;
}
} 2.后缀表达式求值
和括号匹配的整体思路一样,都是在On的时间复杂度内遍历,遇到不同的情况给出不同的解决方案或处理策略
遇到数字时,尝试一直向后,得到整个数字,最后再判断前面是否为负号,并入栈
遇到操作符时,出栈两个进行相应操作,如遇到负号且符号后面有数字则跳过,因为其不是操作符号
遇到空格就跳过
遇到#号就结束
3
对每天的数,只要不是最后一条都入队列,同时出队所有比它小的元素
用栈的思路就是,如果栈为空,就入栈;
如果不空,就要判断此时栈顶元素(先前买的价格)和现在的价格的大小
如果前者小,就一直删,直到删空或者遇到比现在大的
如果前者大,就直接入栈,不卖之前的
这样就能保证栈的元素总是能保持为每一天之后的最大股票价,因为小的已经都出去了
#include
using namespace std;
#include
int main()
{
long long N;
cin>>N;
long long expenditure=0;//总支出
long long income=0;//总收入
stackdiminish;//股票从高到低排序的堆栈
long long stock;//每天的股票价钱
for(long long i=0;i>stock;
expenditure+=stock;//除最后一天不买之外,其它天每天都买进且只买一支股票
if(diminish.empty())//空
{
diminish.push(stock);
}
else if(diminish.top()>=stock)//非空且大
{
diminish.push(stock);
}
else if(diminish.top()>stock;//第N天
while(!diminish.empty())//到最后一天还有没卖掉的,就全部出售。
{
income+=stock;
diminish.pop();
}
cout< 优先队列的思路也同理,只不过换种说法
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
//
int n, num;
long long pout = 0, pin = 0;
priority_queue, greater >q;
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> num;
int cnt = 0;
if (i != n) {
while (!q.empty()) {
if (num > q.top()) {
q.pop();
cnt++;
}
else {
break;
}
}
}
else {
cnt = q.size();
}
pin += cnt * num;
if (i != n) {
pout += num;
q.push(num);
}
}
cout << pin - pout << endl;
return 0;
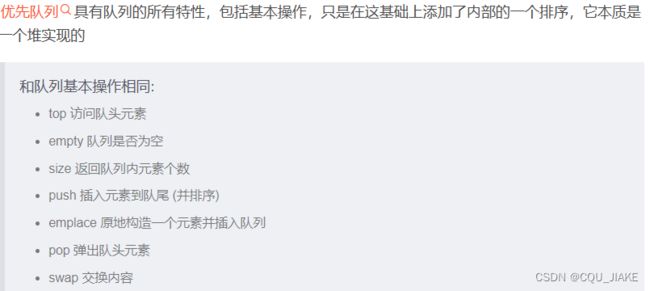
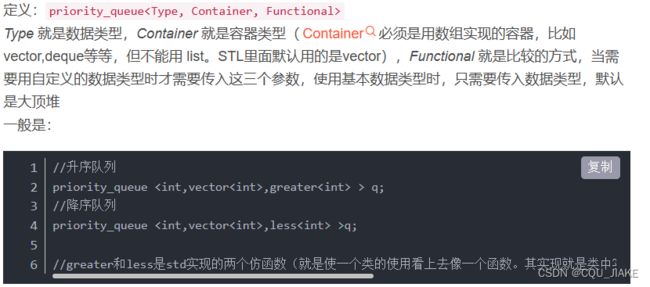
} 优先队列复习
默认为大顶堆,即顶端为最大的;
小木棍1120
贪心思路是让最长的尽可能匹配上最小的
?但是应该是几根拼呢?
要假设一个最短长度,然后从最短长度往下开始搜索,这个最短长度最大应该从最大和次大的和开始,这样可以保证剩下的都没有必要超过
?怎么保证这样拼完之后的长度都相等?即搜索的方式是什么?
前者可以理解成搜索的限制条件,即结果的一个要求
?怎么判断当下长度能不能满足?
所有小木棍有一个长度和,最后拼成的大木棍的数量是一个整数,那么其长度自然是长度和/最后拼成的数量
最后拼成的数量=1,2……
拼成的数量越多,即越往后遍历(外层循环次数越多),大木棍长度越短
枚举的终点就是大木棍长度和最长的长度相等,再短就不可能了
为1时就是全都拼在一起,可能,即这些小木棍拼不出相同长度的大木棍
知道大木棍长度后就开始深搜,排好序从大到小开始,从左往右搜,遇到用过的就c,没用过时就和当前的大木棍剩余长度比比,看能不能拼上去,能就下一层,不能就接着往后,如果最终拼不成
?最终拼不成怎么办?回溯到哪?
就回溯到上一个用的木棍,不用那个木棍
由于存在相同长度的木棍,所以在回溯时不能简单的直接下标++,需要数据预处理,即找到这个长度木棍紧邻的下一个不同长度木棍的编号。
最后一个优化是,如果没拼成,就看此时剩余长度和一些量的关系,用这个长度的木棍还没拼成时,
如果剩余长度和这个木棍长度相同,即用这个木棍拼好了一个大木棍,但是后续的小木棍拼不出整数的大木棍,则说明建立在之前的这么选是不对的
如果剩余长度和大木棍长度相同,即在选第一个木棍时,第一个木棍肯定是要用的,但是在之前拼好的大木棍下,建立在之前的已经用过的剩余最长木棍下拼不出剩下的大木棍,则说明之前选的不对,使后续接着拼木棍遭到了困难,所以也要回溯
整体的思路就是外循环确定大木棍长度,然后小木棍按长度排序,开始搜索拼接,尝试拼成这个大木棍,