CS224W摘要11.Reasoning over Knowledge Graphs

CS224W: Machine Learning with Graphs
公式输入请参考： 在线Latex公式
本节课将介绍知识图谱上的推理任务（就是QA任务）。
主要思路如下：
1.基本概念
2.单跳查询（问答）
3.多跳查询
4.在不完整的KG上进行路径查询（借鉴TransE）
5.联合查询
6.在不完整的KG上进行联合查询（使用Query2Box）
7.Query2Box推广到更一般的形式
本节课用到的一个医学知识图谱。

Reasoning over Knowledge Graphs

Predictive Queries on KG

给出几个例子：

Query Types	Examples
One-hop Queries	What adverse event is caused by Fulvestrant? (e:Fulvestrant, (r:Causes))
PathQueries	What protein is associated with the adverse event caused by Fulvestrant? (e:Fulvestrant, (r:Causes, r:Assoc))
Conjunctive Queries	What is the drug that treats breast cancer and caused headache? ((e:BreastCancer, (r:TreatedBy)), (e:Migraine, (r:CausedBy))

从One-hop query到path queries（完整KG）

对于单跳查询，可以说非常简单，因为在KG里面已经有$(h,r,t)$的三元组了，这个时候的单跳查询相当于：问题$(h,(r))$的答案是$t$吗。
For example: What side effects are caused by drug Fulvestrant?
例如：张三的爸爸是谁？
然后可以把单跳查询扩展到多跳查询，就是加多个关系进行计算，多个关系就会形成路径（path）
$$q=(v_a,(r_1,\cdots ,r_n))$$
其中$v_a$是开始实体（anchor entity）,后面那些就是路径。
答案可以记为：$[[q]{]}_G$
图形化后：

例子：燕小六的七舅姥爷的三外孙女
“What proteins are associated with adverse events caused by Fulvestrant?”
$v_a$ is e:Fulvestrant
$r_1,r_2$ is (r:Causes, r:Assoc)
Query:(e:Fulvestrant, (r:Causes, r:Assoc))

做这个查询就是用图的遍历即可，先遍历第一步$r_1$：

遍历第二步$r_2$：

但是实际上没有这么简单，因为KG是不完整的。
例如：如果Fulvestrant和Short of Breath之间少了一个关系，那么会导致最后结果少了一个。

为什么不先做KG Completion

根据上节学习到的知识，我们知道可以做知识图谱补全任务，是不是补全了之后再来做推理就完美了？
答案：不是的
因为在知识图谱补全任务中，得到的补全的结果是一个非常稠密的图，补全任务中得到的关系是一个概率，所以大多数节点都会有一定概率出现关系（边）。
Time complexity of traversing a dense KG is exponential as a function of the path length ：$O(d_{max}^L)$

可以看到遍历操作是指数级别的复杂度，玩不起。下面看解决方案。

Answering Predictive Queries on Knowledge Graphs

Task: Predictive Queries

要在缺失信息（边）的情况下作出回答，相当于：Generalization of the link
prediction task
核心思路：
根据TransE的socore函数：
$$f_r(h,t)=-||h+r-t||$$
可以把查询的表征理解为：$q=h+r$
那么Predictive Queries的目标就是要使得查询的表征与答案的表征越近越好。
$$f_q(t)=-||q-t||$$
同样套路，先看单跳查询：

如果是多跳查询：$q=(v_a,(r_1,\cdots ,r_n))$

这样做的好处：
The embedding process only involves vector addition, （向量的加法）$\text{independent of \# entities}$ in the KG!
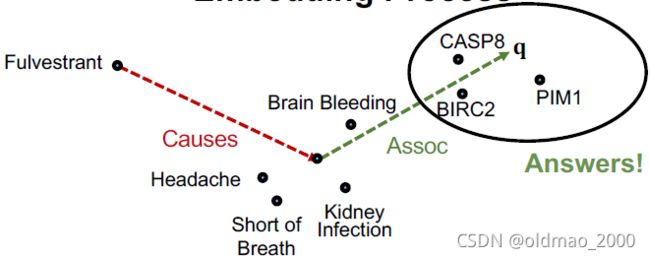
看例子：“What proteins are associated with adverse events caused by Fulvestrant?”
查询表示为： (e:Fulvestrant, (r:Causes , r:Assoc))

步骤	Query Plan	Embedding Process
1
2
3

这里要补充1点：由于几个KG补全模型中，只有TransE能处理composition
relations，TransR / DistMult / ComplEx则不行。

Conjunctive Queries（完全图）

对于更加复杂的Conjunctive Queries，上面的模型就不好用了，看例子：
“What are drugs that cause Short of Breath and treat diseases associated with protein ESR2?”
查询：((e:ESR2, (r:Assoc, r:TreatedBy)), (e:Short of Breath, (r:CausedBy))
Query plan:

按KG traversal的思路，把这个Conjunctive Queries分解为两个Path Queries，然后求公共区域（不是求交）：

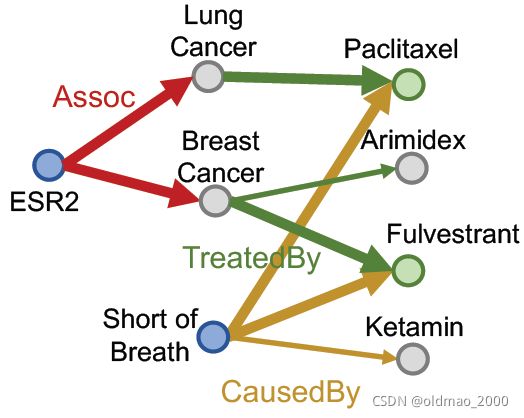
这也是在完全图的视角下完成的，如果缺少某个边，那么还是不行：

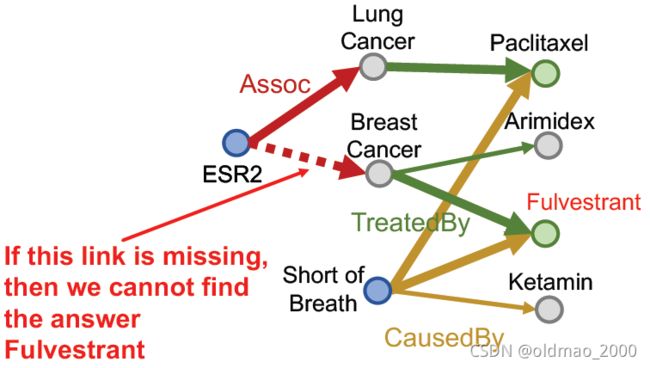
Query2box: Reasoning over KGs Using Box Embeddings

再回过头来看这个图，实际上这里面的灰色三个点实际上可能包含多个实体，解决这个表达 就要用框。

Box Embedding

Embed queries with hyper-rectangles (boxes)
$$\mathbf{q}=(Center(q),Offset(q))$$
如果玩过数据库的QR Tree索引就会比较好理解，就是用一个矩形框来表征几个实体，例如：we can embed the adverse events of Fulvestrant with a box that enclose all the answer entities.

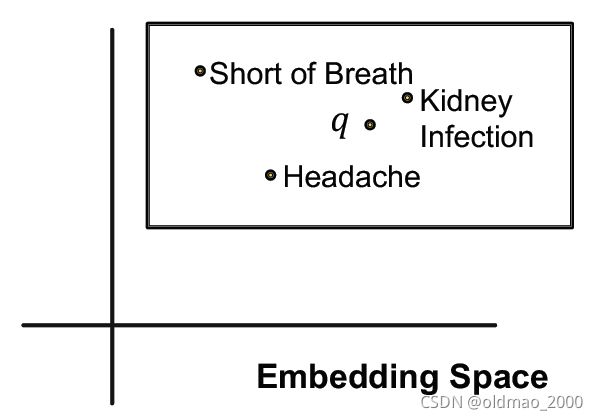
对于一些特殊的表示：
1.单个实体可以看做offset为0的矩形框，就是一个点。
2.每个关系会产生一个新的矩形框
3.多个矩形框可以做交集操作，得到的仍然是一个框（可以是空）
看上面的例子：
“What are drugs that cause Short of Breath and treat diseases
associated with protein ESR2?”
查询：((e:ESR2, (r:Assoc, r:TreatedBy)), (e:Short of Breath, (r:CausedBy))
再次看：

	Query Plan	Embedding Space
1
2
3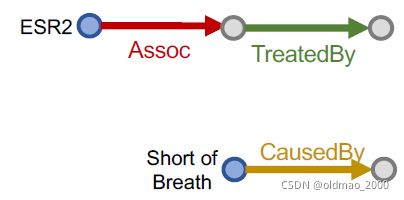

Projection 和Intersection

这里补充一下从点（或者矩形框）通过关系得到新box的操作：Projection Operator $\mathcal{P}$
Box × Relation → Box
$$\begin{gathered} Cen(q^{\prime })=Cen(q)+Cen(r) \\ Off(q^{\prime })=Off(q)+Off(r) \end{gathered}$$

然后还有求相交操作Geometric Intersection Operator $\mathcal{J}$
Take multiple boxes as input and produce the intersection box.
求相交后的结果小于等于原来Box的面积，相交结果的中心应尽量接近求交的矩形中心。
这个求相交操作也是分别求相交后的结果的面积和中心两个部分。
对于中心：以输入矩形的中心做加权求和后作为新矩形中心。看下图的红色部分。
对于面积：是三个投影相交的公共部分。看下图的阴影部分。

求中心的数学表达：

$w_i\in {\mathbb{R}}^d$ is calculated by a neural network $f_{cen}$ (with trainable weights)
这里老师还给出了$w_i$的另一种解释，相当于自注意力机制权重，从上面的图可以看到，面积大的那么新中心离其越近。实际上上面的$w_i$就是走的softmax公式，就是算权重。
求Offset（相交阴影）的表达如下：
$$Off(q_{inter})=\min \left(off(q_1),\cdots ,off(q_n)\right)\odot \sigma (f_{off}(off(q_1),\cdots ,off(q_n)))$$
前面一项是找出所有输入矩形框中最小的那个。
$f_{off}$ is a neural network (with trainable parameters) that extracts the representation of the input boxes to increase expressiveness.
这里用到了sigmoid函数（值域是(0,1)），保证求相交后的面积变小。

实体到Box的距离表达

这里的Entity-to-Box 距离用$f_q(v)$表示。该距离是一个负数
Given a query box and entity embedding (box) ,
$$d_{box}(q,v)=d_{out}(q,v)+\alpha \cdot d_{in}(q,v),0<\alpha <1$$

$f_q(v)=-d_{box}(q,v)$
这里不是直线距离，看图：

有了这个距离表达，就可以将最终的查询进行量化。
上面讲的求交集的操作，下面扩展一下，看求并集的操作。
Conjunctive queries + disjunction is called Existential Positive First-order (EPFO) queries. We’ll refer to them as AND-OR queries.

AND-OR queries

先说结论：可以做，但是不能直接做
先来看为什么不能直接做（需要高维向量才能表示结果，这和我们用DL的目标相悖）。

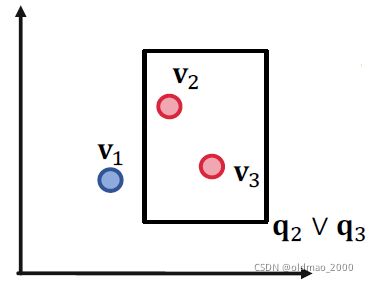
Example for 3 queries with union operation

Given 3 queries $q_1,q_2,q_3)$, with answer sets:
$$[[q_1]]=\{v_1\},[[q_2]]=\{v_2\},[[q_3]]=\{v_3\}$$
We want red dots (answers) to be in the box while the blue dots (negative answers) to be outside the box.
先看如果只考虑一个查询的情况：

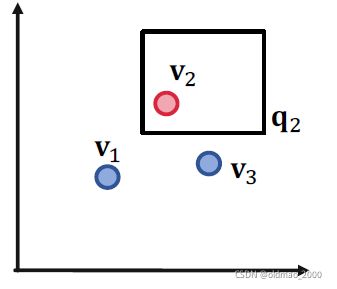
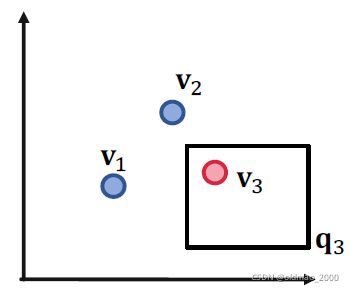
没有问题，再看两个查询的情况：

也没有问题，说明三个查询在二维情况下都木有问题。

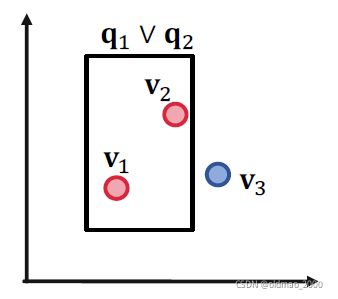
Example for 4 queries with union operation

Given 4 queries $q_1,q_2,q_3,q_4)$, with answer sets:
$$[[q_1]]=\{v_1\},[[q_2]]=\{v_2\},[[q_3]]=\{v_3\},[[q_4]]=\{v_4\}$$

这下出问题了，在二维空间中没有办法单独框出$v_2,v_4$
除非在三维空间才可以。
因此推出结论：对于AND-OR queries 无法在低维空间进行表征。

Given any conjunctive queries $q_1,\dots ,q_M$ with non-overlapping answers, we need dimensionality of $\Theta (M)$ to handle all OR queries.

这还是任意一个OR查询而已。。。

解决之道

take all unions out and only do unionat the last step!

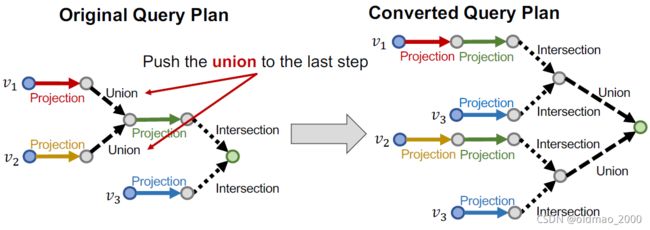
这样做的好处就无论多么复杂的查询，都把Union操作放到最后，写成一般形式：
Any AND-OR query can be transformed into equivalent DNF(disjunctive normal form) , i.e., disjunction of conjunctive queries.
$$q=q_1\vee q_2\vee \cdots \vee q_m$$
where $q_i$ is a conjunctive query.
对于实体和上面的一般表达式的距离可以表示为：
$$d_{box}(q,v)=\min (d_{box}(q_1,v),\cdots ,d_{box}(q_m,v))$$
理解这个公式很重要，就是破解低维空间表达向量的关键。
$q_i$是$q$的子集，如果$v$是$q_i$的某个答案，那么也是$q$的答案；
同理，在向量空间中，如果$v$与$q_i$很接近，那么也和$q$很接近。

The process of embedding any AND-OR query

1. Transform to equivalent DNF $q_1\vee q_2\vee \cdots \vee q_m$
2. Embed $q_1$ to $q_m$
3. Calculate the (box) distance $d_{box}(q_i,v)$
4. Take the minimum of all distance
5. The final score $f_q(v)=-d_{box}(q,v)$

Training

主要思想还是constrative loss，最大化正样本的分数，最小化负样本的分数。
涉及到的参数有：
Entity embeddings with $d|V|$ # params
Relation embeddings with $2d|R|$ # params
Intersection operator
步骤：

1. Randomly sample a query $q$ from the training graph $G_{train}$, answer $v\in [[q]{]}_{G_{train}}$, and a negative sample $v^{\prime }\notin [[q]{]}_{G_{train}}$.
   Negative sample: Entity of same type as $v$ but not answer.
2. Embed the query $q$.
3. Calculate the score $f_q(v)$ and $f_q(v^{\prime })$.
4. Optimize the loss $l$ to maximize $f_q(v)$ while minimize $f_q(v^{\prime })$:
   $$\ell =-\log \sigma \left(f_q(v)\right)-\log (1-\sigma (f_q(v^{\prime })))$$

Query generation from templates

query抽象后就是query template.
Start from instantiating the answer node of the query template and then iteratively instantiate the other edges and nodes until we ground all the anchor nodes.
思想就是反过来，从答案往anchor方向回溯。
下面看从KG抽象query的过程：

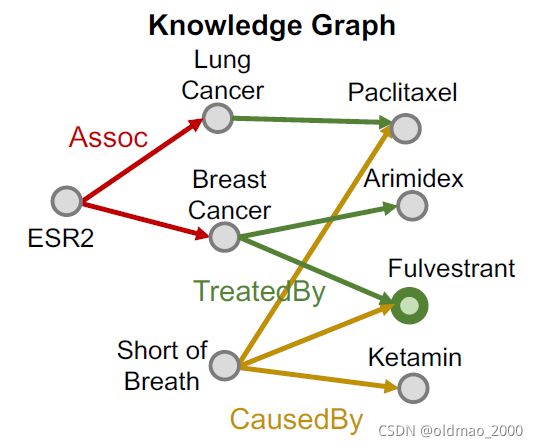
1.先初始化一个root node，这里选Fulvestrant
跟Fulvestrant有关的的有黄线和绿线
2.随机选一个，例如选中了绿色的TreatedBy，然后根据TreatedBy得到实体：Breast Cancer

3.然后再根据实体Breast Cancer的Assoc边找到Anchor：ESR2

4.然后再按同样的思路从Fulvestrant走黄线CausedBy得到另外一个Anchor：Short of Breath

5.最后得到查询$q$

查询的表达：
: ((e:ESR2, (r:Assoc, r:TreatedBy)), (e:Short of Breath, (r:CausedBy))
注意要点：
1.The query must have answers on the KG and one of the answers is the instantiated answer node: Fulvestrant.
2.We may obtain the full set of answers $[[q]{]}_{G_{}}$ by KG traversal.
3.We can sample negative answers $v^{\prime }\notin [[q]{]}_{G_{}}$

可视化实例

Example: “List male instrumentalists who play string instruments”
用tsne降维后显示结果。

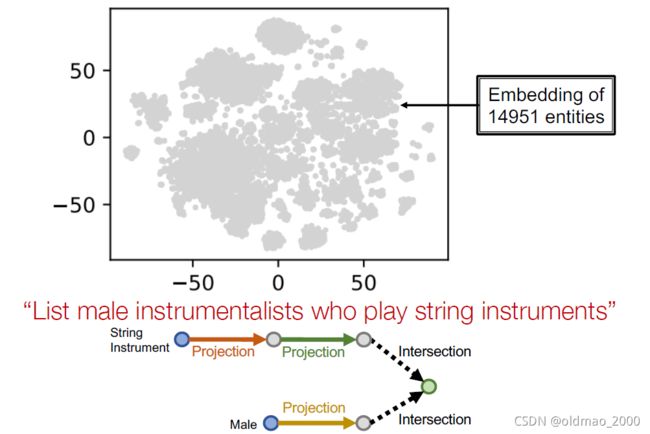
先找锚点

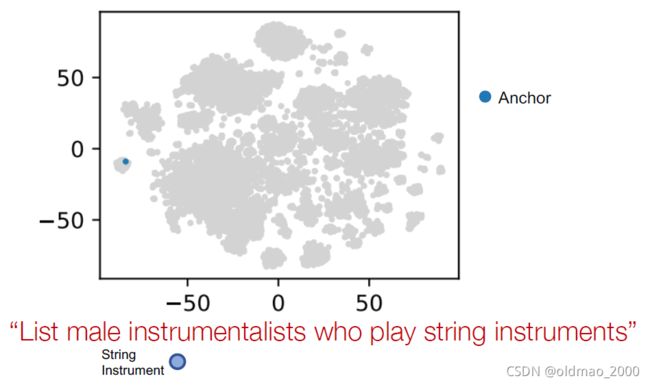
然后这里做projection操作后，可以看到准确率100%

再一次projection：

另外一个锚点Male：

projection

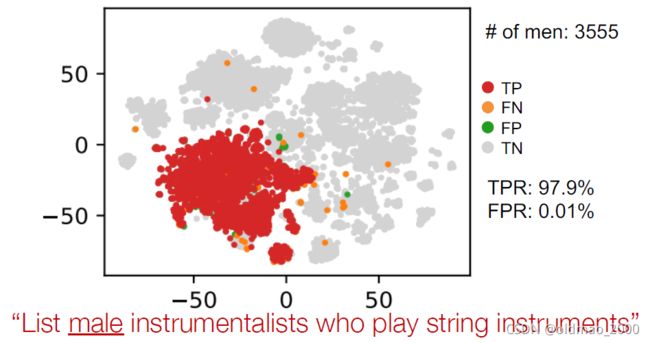
最后做intersection