最简单的算法:线性查找法
目录
写在前面
一、什么是算法
二、线性查找法
2.1、实现线性查找法
2.2、思维拓展——使用泛型
2.3、自定义类测试泛型方法
2.4、循环不变量
三、复杂度分析
3.1、复杂度分析简介
3.2、常见的算法复杂度
四、算法性能测试
写在前面
最近比较忙,并且近期还要完成人生的一件大事,所以文章最近写的比较少,今天抽空整一篇,贵在坚持吧!
当你在这个行业摸爬滚打几年之后,或许你会像我一样感到迷茫,想进入大厂工作,当你真正去大厂面试的时候,你会发现所有大厂的面试都无可避免的会问到数据结构与算法相关的知识,这是为什么呢?这些东西真的有那么重要吗?为什么我平时也没用到不照样写项目吗?灵魂三连击啊,没办法,现实就是这么残酷。当然了原因其实也很简单,因为现在的计算机科学处于一个高速发展的时代,对于公司业务层面的日常开发都是依赖于各种开发框架、数据库软件、工具库等等,你觉得没用到,那是因为别人已经帮你搞好了,晓得了吧,而大厂面试并不是说看你能不能做业务,能做业务的人多了,凭什么选你呢,你是比别人长得好看吗?他们更多的是注重个人基础能力和未来的发展潜力以及对新知识的学习能力,所以没啥好抱怨的。
如果你大学是读计算机专业的,那么你肯定知道数据结构和算法是必学的课程,我不知道还是否有人记得,大学计算机基础里面对于程序的定义是什么?还有人记得吗?没错,程序 = 数据结构 + 算法,不信的话你可以回去翻翻看。
上面废话了这么多,就是想表明数据结构和算法的重要性(虽然我也不会,但是咱得有这个意识),所以我新开了一个专栏用来记录我的数据结构和算法的学习之路,下面这张图里面罗列了一些很重要的数据结构和算法,当然还有一块没有列出,有人能想到是什么吗?图论,它也是很重要的一块知识点,后面等学到了再单独介绍,大家可以看看这张图感受一下:
今天我们就从最简单的来看——线性查找,这个我相信99%的人应该都写过,所以难度等级---简单。
一、什么是算法
英文对应的单词是Algorithm,它的本意为:解决问题的方法,所以算法的直接理解就是解决问题的方法。在计算机领域定义的话就是:一系列解决问题的、清晰、可执行的计算机指令。
在我们的日常生活中,到处都是算法,它就在你身边,你却没发现,其实也不是没发现,只是你没给它定义为算法这个概念而已,举几个常见的栗子,比如:问路(如何去新街口)、菜谱(糖醋里脊这道菜怎么做),这些问题的解决方案都可以当做是一个小的算法。下面来简单了解一下算法的几个特性(了解即可):
算法的五大特性
- 有限性:在有限的时间内可以执行完成(有限的时间并不一定是非常短的时间)
- 确定性:不会产生二义性,描述该算法的每个指令的含义都是清晰的
- 可行性:算法中的每一步指令都是可行的
- 输入(输入输出在理解层面上是一种更加广义的概念)
- 输出
今天由于是第一篇,咱们来看一个最简单的算法:线性查找法。
二、线性查找法
2.1、实现线性查找法
线性查找法在生活中其实是很常见的,举个栗子吧:比如,你的书架上第一层有许多书,现在你想要从里面找到《编译原理》这本书,你会怎么找呢?通常你会从第一本开始看书名,如果是的就找到了直接拿出来,如果不是就继续下一本,以此类推,其实这样一个过程就是线性查找的过程。
下面我们就通过一个实际的案例,然后来看看实现这样一个线性查找,代码究竟该怎么写?
针对上面这个案例,相信大家立马就能想到该如何实现了?没错,就是一个简单的for循环,没啥好讲的,直接上代码了:
public class LinearSearch {
//私有构造,防止外部实例化该对象
private LinearSearch(){}
//线性查找元素
public static int search(int[] data, int target) {
for (int i = 0; i < data.length; i++) {
if (data[i] == target) {
return i;
}
}
return -1;
}
//测试方法
public static void main(String[] args) {
int[] data = {2, 9, 5, 1, 8, 7, 3, 6};
int index = LinearSearch.search(data, 8);
System.out.println(index);
}
}
2.2、思维拓展——使用泛型
上面的程序我们实现了一个最基础最简单的整型数组的线性查找算法,现在我们来进一步的思考,将这个业务场景进一步的发散,在实际的应用中,你可能遇到的数据类型不是整型的,比如字符型、浮点型甚至是自定义的Object类型,如果是这样的话很显然,上面的程序就无法满足了,可能你就会根据对应的业务场景把上面的代码再Copy一份,然后对应的修改为你需要的类型,这样写没什么问题哈,需求当然也是能实现的,但是这个实现的方式有点......,不说了自己体会吧,我就是那么干的。
实际上我们不必如此,你想啊,如果能使用一个万能的类型不就搞定了吗,你在调用的时候业务方是什么类型你就传什么类型,程序的可扩展性是不是极大的提高了,而且你也不用再复制出来那么多重复操作的代码了,所以思维方式决定了代码行数啊!
好,下面来说解决方案,基本上在每种程序语言中都有一个专门的语言特性是用来处理这种问题的,它可以让你的类或者是方法能够处理不同的类型,这种机制就是——泛型,关于泛型的基本用法这里不做介绍,因为咱不是来说语言的哈,所以下面就来把上面的代码通过泛型进行改造。
首先我们不会直接将LinearSearch这个类定义为泛型类,因为那样没有意义,我们直接操作的是该类中定义的search()方法,所以应该将这个方法改造为泛型方法。
这里简单的对Java中的基本数据类型做一个补充:
- Java语言中使用泛型,不可以是基本数据类型,只能是类对象
- Java中八种基本数据类型:boolean,byte,char,short,int,long,float,double
- 每个基本数据类型都有对应的包装类
- 对应的包装类:Boolean,Byte,Character,Short,Integer,Long,Float,Double
下面来看改造为泛型方法后的代码是什么样的呢?如下所示,很简单哈:
public class LinearSearch {
//私有构造,防止外部实例化该对象
private LinearSearch(){}
//线性查找元素,泛型只能接受类对象,不能接受基本数据类型
public static int search(T[] data, T target) {
for (int i = 0; i < data.length; i++) {
//"=="判断的是引用相等,我们需要判断的是值相等,所以这里用equals()方法
if (data[i].equals(target)) {
return i;
}
}
return -1;
}
//测试方法
public static void main(String[] args) {
//转换成对应的包装类
Integer[] data = {2, 9, 5, 1, 8, 7, 3, 6};
//target仍然可以传递数字,因为Java中有自动转换机制,编译器自动转换为对应的包装类
int index = LinearSearch.search(data, 8);
System.out.println(index);
}
} 这段代码执行的结果和上面是一样的,仍然是4。
2.3、自定义类测试泛型方法
上面改造完成之后,咱们测试仍然用的是基本数据类型,如果你想要使用自定义的类来测试上面的方法好不好用,有一点需要注意,你必须自己去重写equals()方法的逻辑,基本数据类型中是Java语言已经帮我们实现好了,所以自定义类需要你自己实现,这个任务在逻辑结构上不属于search()方法需要完成的任务,它是自定义类的设计者要去完成的,所以咱们的search()方法不需要做任何改动,下面来举个栗子实际操作一下。
比如,这里自定义一个类:Beauty,给她一个成员变量name,然后我们先不重写equals()方法,如下:
public class Beauty {
private String name;
public Beauty(String name){
this.name = name;
}
}然后在main()方法中使用该类进行测试:
public static void main(String[] args) {
Beauty[] beauties = {new Beauty("杨幂"),new Beauty("赵丽颖"),new Beauty("唐嫣")};
Beauty beauty = new Beauty("赵丽颖");
int result = LinearSearch.search(beauties,beauty);
System.out.println(result);
}执行结果为-1,虽然name一样,但是却查不到,因为没有重写equals(),它就没有name一样就是同一个对象的逻辑,就会执行默认的比较逻辑,equals()默认比较的是两个类对象的地址:
现在我们来实现自己的比较逻辑,重写equals()方法,让它实现name相同即为同一个对象的功能:
public class Beauty {
private String name;
public Beauty(String name) {
this.name = name;
}
@Override
public boolean equals(@Nullable Object obj) {
if (this == obj)
return true;
if (obj == null)
return false;
if (this.getClass() != obj.getClass())
return false;
Beauty beauty = (Beauty) obj;
return this.name.toLowerCase().equals(beauty.name.toLowerCase());
}
}此时,同样的main()方法,你再运行就可以查到对应的下标啦:
2.4、循环不变量
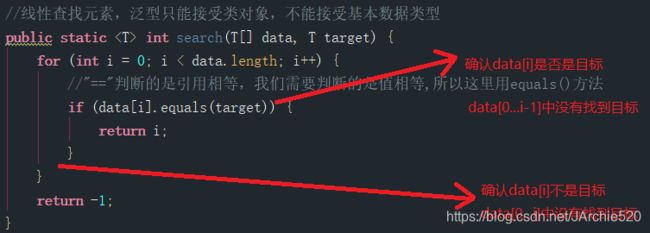
首先来看下面这张图,图中我做了一些简单的标注,相信都能看懂是什么意思:
循环不变量的概念就是:在每一轮循环开始时,算法都满足data[0...i-1]中没有找到目标这个条件,这就叫循环不变量,循环体即if语句它所做的事情就是在维持着循环不变量。简单来说,循环不变量就是在算法每一轮开始都保持着一个什么样的特性,而循环体则是在维持这个特性。由于咱们这个算法比较简单,所以你可能看不出循环不变量有什么用,当你在设计一些相对复杂的算法的时候,你可能就能够看到循环不变量的意义所在了,这里的话对这个概念有个基本的了解即可。
三、复杂度分析
3.1、复杂度分析简介
首先来看下图,这是上面咱们写的那个算法,对于一个算法性能的评估,通常我们要去考虑最差的情况:
时间复杂度是算法运行时间与数据规模n之间的关系,当一个算法满足:T=k*n+m这个表达式,则认为它的时间复杂度是O(n),从这个表达式也能看出,常数不重要,复杂度描述的是随着数据规模n的增大,算法性能的变化趋势,举个例子,如下图中所示,两种复杂度分析:
3.2、常见的算法复杂度
- 线性查找法:O(n)
- 一个数组中的元素可以组成哪些数据对:O(n²)
- 遍历一个n*n的二维数组:O(n²)
- 数字n的二进制位数:O(logn) 对应的进制为底数
- 数字n的所有约数:O(n)或者O(√n)
- 长度为n的二进制数字:
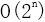
- 长度为n的数组的所有排列:O(n!)
- 判断数字n是否是偶数:O(1)
上面说的这些其实都是从时间的角度来说的,所以都是时间复杂度。实际上空间也是有复杂度的,原理跟上面相同,就是看它开辟额外的空间的大小和数据规模n之间的关系,表示符号和上面一样,比如我们的线性查找法它的空间复杂度就是O(1)。
四、算法性能测试
在这一部分咱们来对我们上面写的算法做一个性能测试,通过构造较大的数据量来测试算法执行的性能。
首先,我们来写一个构造数据的类ArrayCreator:
public class ArrayCreator {
private ArrayCreator(){}
public static Integer[] creatorArray(int n){
Integer[] arr = new Integer[n];
for (int i=0;i接着在main()方法中分别构造100万条数据和1000万条数据并且分别执行100次,在自己的计算机上面跑一下来看程序执行时间:
public static void main(String[] args) {
int[] dataSize = {1000000, 10000000};
for (int n : dataSize) {
Integer[] data = ArrayCreator.creatorArray(n);
long startTime = System.nanoTime();
for (int k = 0; k < 100; k++)
LinearSearch.search(data, n);
long endTime = System.nanoTime();
double time = (endTime - startTime) / 1000000000.0;
System.out.println("n=" + n + ",运行100次耗时:" + time + "秒");
}
}本地计算机执行结果:
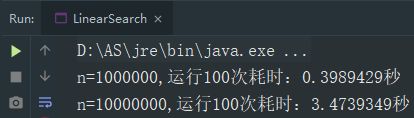
从上面的执行结果我们可以看到,1000万条数据的执行时间大致是100万条数据的10倍,这根咱们的数据量级也是基本成正比的,当然了,这个跟你的计算机性能也是有关的,我这台计算机的配置也还算可以了,不同的计算机执行的结果可能会稍有不同,大家可以自行进行测试。
写到这里,咱们今天的算法开篇就算是说完了,介绍了一个最简单的算法,其实都不能说它是个算法,然后介绍了一下复杂度的简单定义,如果你需要相对完整清晰的理论可以去自行查找一下相关的资料,入门级的书籍有一本国外的《算法导论》可以看一下。
好了,今天就到这里吧,最近有点忙更的少了,抱歉!
祝:工作顺利!