力扣每日一题刷题总结：二叉树篇

100. 相同的树 Easy 递归 2022/3/23

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

最牛递归，判断其左子树和右子树是否均相同来判定树是否相同，难点在于写全边界条件：均为空返回真。有一方为空一方不为空返回假，都不为空如值不相等则为假。

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p==nullptr && q==nullptr) return true;
        else if(p==nullptr || q==nullptr) return false;
        else if(p->val != q->val) return false;
        else return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
    }
};

---

98. 验证二叉搜索树 Medium 递归 2022/3/24

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

递归法，设上下界进行比较。对于左子树进行递归，将上界设为原root，下界不动；对于右子树进行递归，将下界设为原root，上界不动。

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return recur(root, nullptr, nullptr);
    }
    bool recur(TreeNode* root, TreeNode* min, TreeNode* max){
        if(root==nullptr) return true;
        if(min!=nullptr && min->val >= root->val) return false; //如果有下界且下界值大于等于当前节点值
        if(max!=nullptr && max->val <= root->val) return false; //如果有上界且上界值小于等于当前节点值
        //对于左子树进行递归，将上界设为原root，下界不动；对于右子树进行递归，将下界设为原root，上界不动
        return recur(root->left, min, root) && recur(root->right, root, max); 
    }
};

---

700. 二叉搜索树中的搜索 Easy 递归 2022/3/24

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

方法一：最简单的递归，没有考虑二叉搜索树的特性。

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root==nullptr) return nullptr;
        if(root->val==val) return root;
        //递归左子树，如果找到则返回
        TreeNode* result = searchBST(root->left, val);
        if(result!=nullptr) return result;
        //递归右子树
        else return searchBST(root->right, val);
    }
};

方法二：利用二叉搜索树左树值小于结点值小于右树所有值的特性，轻松实现递归，比方法一省掉了一半的判断。

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root == nullptr) return nullptr;
        if(root->val == val) return root;
        //如果当前结点值大于val，则递归左子树
        if(root->val > val) return searchBST(root->left, val);
        //递归右子树
        else return searchBST(root->right, val);
    }
};

---

701. 二叉搜索树中的插入操作 Medium 递归 2022/3/24

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。

递归法，找到空的结点区域进行插入即可。

class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        //找到了空的结点区域，new一个结点返回
        if(root == nullptr)
            return new TreeNode(val);
        //二叉搜索树框架
        if(root->val > val) 
            root->left = insertIntoBST(root->left, val);
        if(root->val < val) 
            root->right = insertIntoBST(root->right, val);
        return root;
    }
};

---

226. 翻转二叉树 Easy 递归 2022/3/24

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

使用模板思想，写好边界条件即可。

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root==nullptr) return nullptr; //边界条件
        //交换左右结点
        TreeNode* temp = root->left;
        root->left = root->right;
        root->right = temp;
        //递归交换左右子树
        invertTree(root->left);
        invertTree(root->right);
        return root;
    }
};

---

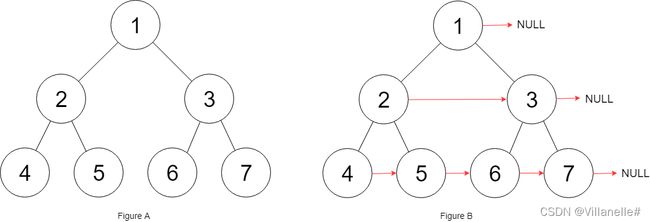
116. 填充每个节点的下一个右侧节点指针 Medium 递归 2022/3/24

给定一个 完美二叉树（即满二叉树） ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
	int val;
	Node *left;
	Node *right;
	Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。

由于单独使用一个结点无法连接不同子树的结点，使用辅助函数连接两个结点解决。

class Solution {
public:
    Node* connect(Node* root) {
        if (root == nullptr) return root;
        connectTwoNodes(root->left, root->right);
        return root;
    }
    //由于单独使用一个结点无法连接不同子树的结点，使用辅助函数
    void connectTwoNodes(Node* root1, Node* root2){
        if (root1 == nullptr) return;
        //连接当前层
        root1->next = root2;
        //连接下一层兄弟结点
        connectTwoNodes(root1->left, root1->right);
        connectTwoNodes(root2->left, root2->right);
        //连接下一层非兄弟结点
        connectTwoNodes(root1->right, root2->left);
    }
};

---

114. 二叉树展开为链表 Medium 递归 2022/3/24

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

使用递归，套用二叉树遍历框架（后序遍历），分三步：将左子树和右子树拉平，将现左子树置空，原左子树接到根节点上并与右子树相连。无需考虑是如何实现的！只需要写清楚逻辑即可。

class Solution {
public:
    void flatten(TreeNode* root) {
        if (root == nullptr) return;
        // 先把左右子树都拉平
        flatten(root->left);
        flatten(root->right);
        // 保存左右子树根节点
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        // 左子树置空，右子树放原左子树的根节点
        root->left = nullptr;
        root->right = left;
        // 找到当前树的叶子结点
        TreeNode* p = root;
        while(p->right != nullptr){
            p = p->right;
        }
        p->right = right;
    }
};

---

543. 二叉树的直径 Easy 递归 2022/3/24

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

递归法，直径=左右子树的最大深度之和。定义辅助函数求结点的最大深度，并实时更新(顺带求一下)最大直径长度。

class Solution {
public:
    int maxDiameter = 0;
    int diameterOfBinaryTree(TreeNode* root) {
        traverseDepth(root);
        return maxDiameter;
    }
    // 辅助函数，用于计算每个结点的最大深度，并实时更新最大直径长度
    int traverseDepth(TreeNode* root){
        // 空结点的最大深度长度定为0
        if (root == nullptr) return 0;
        int leftDepth = traverseDepth(root->left);
        int rightDepth = traverseDepth(root->right);
        // 更新最大直径长度为两个子结点最大深度之和(每个结点都一定会遍历到)
        maxDiameter = max(leftDepth + rightDepth, maxDiameter);
        // 返回最大深度
        return max(leftDepth, rightDepth) + 1;
    }
};

---

654. 最大二叉树 Medium 递归 2022/3/25

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
创建一个根节点，其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例：
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]

利用辅助函数，构建根节点，递归构造左右子树。

class Solution {
public:
    // 主函数
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return build(nums, 0, nums.size() - 1);
    }
    // 递归函数
    TreeNode* build(vector<int>& nums, int first, int last){
        if(first > last){
            return nullptr;
        }
        int maxnum = nums[first];
        int index = first;
        // 得到最大值下标和最大值
        for(int i = first; i <= last; i++){
            if (nums[i] > maxnum){
                maxnum = nums[i];
                index = i;
            }
        }
        // 创建根节点
        TreeNode* root = new TreeNode(maxnum);
        // 对左子树和右子树进行递归
        root->left = build(nums, first, index - 1);
        root->right = build(nums, index + 1, last);
        return root;
    }
};

---

105. 从前序与中序遍历序列构造二叉树 Medium 递归 2022/3/27

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。
示例：
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

与构造最大二叉树类似，通过先序遍历确定根节点，再根据中序遍历划分左右子树，递归构造左右子树。注意递归时的参数。

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder){
    return build(preorder, 0, preorder.size() - 1, inorder, 0, inorder.size() - 1);
    }
    // 辅助函数实现递归
    TreeNode* build(vector<int>& preorder, int pfirst, int plast, 
                    vector<int>& inorder, int ifirst, int ilast){
        if (pfirst > plast || ifirst > ilast) return nullptr;
        // 找到根节点的值
        int rootval = preorder[pfirst];
        // 找到根节点在中序遍历中的位置
        int rootindex = 0;
        for (int i = ifirst; i <= ilast; i++){
            if (rootval == inorder[i]){
                rootindex = i;
                break;  
            }
        }
        // 中序遍历中，根节点左边元素个数
        int leftnum = rootindex - ifirst;
        // 生成根节点
        TreeNode* root = new TreeNode(rootval);
        // 左子树和右子树递归构造
        root->left = build(preorder, pfirst + 1, pfirst + leftnum, 
                           inorder, ifirst, rootindex - 1);
        root->right = build(preorder, pfirst + leftnum + 1, plast, 
                            inorder, rootindex + 1, ilast);
        return root;
    }
};

---

106. 从中序与后序遍历序列构造二叉树 Medium 递归 2022/3/28

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。
示例：
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

与上题类似，通过先序遍历确定根节点，再根据中序遍历划分左右子树，递归构造左右子树。通过后序遍历确定根节点，再根据中序遍历划分左右子树，递归构造左右子树。注意递归时的参数。

class Solution {
public:
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder){
        return build(inorder, 0, inorder.size() - 1, postorder, 0, postorder.size() - 1);
    }
    // 辅助函数实现递归
    TreeNode* build(vector<int>& inorder, int ifirst, int ilast, 
                    vector<int>& postorder, int pfirst, int plast){
        if (ifirst > ilast || pfirst > plast) return nullptr;
        // 找到根节点的值
        int rootval = postorder[plast];
        // 找到根节点在中序遍历中的位置
        int rootindex = 0;
        for (int i = ifirst; i <= ilast; i++){
            if (rootval == inorder[i]){
                rootindex = i;
                break;  
            }
        }
        // 中序遍历中，根节点左边元素个数
        int leftnum = rootindex - ifirst;
        int rightnum = ilast - rootindex;
        // 生成根节点
        TreeNode* root = new TreeNode(rootval);
        // 左子树和右子树递归构造
        root->left = build(inorder, ifirst, rootindex - 1, 
                           postorder, pfirst, pfirst + leftnum - 1);
        root->right = build(inorder, rootindex + 1, ilast, 
                            postorder, pfirst + leftnum, pfirst + leftnum + rightnum - 1);
        return root;
    }
};

---

面试题 04.06. 后继者 Medium 二叉搜索树 2022/5/17

设计一个算法，找出二叉搜索树中指定节点的“下一个”节点（也即中序后继）。
如果指定节点没有对应的“下一个”节点，则返回null。
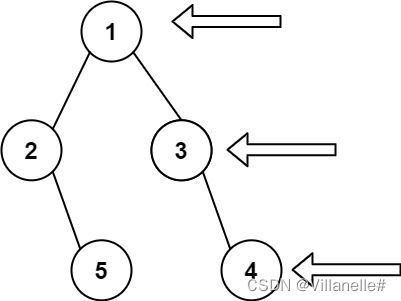
输入: root = [5,3,6,2,4,null,null,1], p = 3

输出: 4

方法一：不考虑二叉搜索树的性质，先中序遍历，将各结点放入容器中，再遍历找到对应结点，返回其后一个结点。

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        vector<TreeNode*> r;
        inorderTraverse(root, p, r);
        r.push_back(nullptr);
        // 找到等于p->val的结点
        for (int i = 0; i < r.size(); i++)
            if(r[i]->val == p->val)
                return r[i + 1];
        return nullptr;
    }
    // 中序遍历，依次将各结点放入vector
    void inorderTraverse(TreeNode* root, TreeNode* p, vector<TreeNode*>& r)
    {
        if (root)
        {
            inorderTraverse(root->left, p, r);
            r.push_back(root);
            inorderTraverse(root->right, p, r);
        }
    }
};

方法二：由于用递归实现中序遍历很难在遍历过程中操作，需要一个额外函数和容器来存放结点，使用栈来实现遍历和一个标志位就可以在遍历的过程中实现下一个结点，但仍没有利用二叉搜索树的性质。

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* s) {
        stack<TreeNode*> stk;
        TreeNode* p = root;
        TreeNode* q = new TreeNode();
        TreeNode* last_node = nullptr;
        bool is_found = false;
        while(p || !stk.empty())
        {
            if (p)
            {
                stk.push(p);
                p = p->left;
            }
            else
            {
                q = stk.top();
                stk.pop();
                // 中序遍历内容
                if (is_found)
                    return q;
                if (q && (q->val == s->val))
                        is_found = true;
                p = q->right;
            }
        }
        return nullptr;
    }
};

方法三：二叉搜索树中左子树<根节点<右子树，如果根节点值小于等于搜寻结点值，其下一个结点一定位于根节点的右子树，如果大于根节点，则可能为根节点，也可能在根节点的左子树上。

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        TreeNode* cur = root;
        TreeNode* res = nullptr;
        while (cur)
        {
            // 当前结点值大于搜寻结点值，则可能为搜寻结点
            if (cur->val > p->val)
            {
                // 保存当前结点观察
                res = cur;
                // 到左子树找
                cur = cur->left;
            }
            // 当前结点小于等于搜寻结点值，到右子树去找
            else
            {
                cur = cur->right;
            }
        }
        return res;
    }
};

---

95. 不同的二叉搜索树 II Medium 后序遍历 分治 2023/2/15

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。
示例：
输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

后序遍历的终极应用——分治
想要构造出所有合法 BST，分以下三步：

1. 穷举 root 节点的所有可能。
2. 递归构造出左右子树的所有合法 BST。
3. root 节点穷举所有左右子树的组合。

class Solution {
public:
    vector<TreeNode*> generateTrees(int n) {
        return generateTrees(1, n);
    }
    vector<TreeNode*> generateTrees(int min, int max) {
        if (min > max) return {nullptr};
        // 枚举可行根节点
        vector<TreeNode*> allTrees;
        for (int i = min; i <= max; i++){
            // 获得所有可行的左子树集合
            vector<TreeNode*> leftTrees = generateTrees(min, i - 1);
            // 获得所有可行的右子树集合
            vector<TreeNode*> rightTrees = generateTrees(i + 1, max);
            // 从左子树集合中选出一棵左子树，从右子树集合中选出一棵右子树，拼接到根节点上
            for (TreeNode* left: leftTrees) {
                for (TreeNode* right: rightTrees) {
                    TreeNode* p = new TreeNode(i, left, right);
                    allTrees.push_back(p);
                }
            }
        }
        return allTrees;
    }
};

---

241. 为运算表达式设计优先级 Medium 后序遍历 分治 2023/2/22

给你一个由数字和运算符组成的字符串 expression ，按不同优先级组合数字和运算符，计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。
示例：
输入：expression = “23-45”
输出：[-34,-14,-10,-10,10]
解释：
(2*(3-(45))) = -34
((23)-(45)) = -14
((2(3-4))5) = -10
(2((3-4)5)) = -10
(((23)-4)*5) = 10

本题不是二叉树题，但其分治思想与上题一模一样！

遍历字符串直到找到一个符号，将其拆分为两个字符串，分别递归计算产生两个数组，对于这两个数组，每次从中取出一个值并进行运算。

base case的分析：如果只有一个元素，即找不到对应的符号，很显然找不到符号，即res为空，此时res即为当前数字值！将其转化为int并放进数组。

最后使用备忘录优化即可，对于已经出现过的子表达式，避免重复运算。

class Solution {
public:
    unordered_map<string, vector<int>> memo;
    vector<int> diffWaysToCompute(string expression) {
        // 备忘录
        if (memo.find(expression) != memo.end()) return memo[expression];
        int n = expression.size();
        vector<int> res;
        for (int i = 0; i < n; i++) {
            char c = expression[i];
            if (c == '+' || c == '-' || c == '*') {
                // 分！以运算符为中心，分割成两个字符串，分别递归计算
                vector<int> left = diffWaysToCompute(expression.substr(0, i));
                vector<int> right = diffWaysToCompute(expression.substr(i + 1, n - i - 1));
                // 治！通过子问题的结果，合成原问题的结果
                for (int l: left)
                    for (int r: right)
                        if (c == '+')
                            res.push_back(l + r);
                        else if (c == '-')
                            res.push_back(l - r);
                        else if (c == '*')
                            res.push_back(l * r);
            }
        }
        // base case
        if (res.empty()) res.push_back(atoi(expression.c_str()));
        memo[expression] = res;
        return res;
    }
};

---

剑指 Offer II 043. 往完全二叉树添加节点 Medium 层序遍历 2023/3/3

完全二叉树是每一层（除最后一层外）都是完全填充（即，节点数达到最大，第 n 层有 2n-1 个节点）的，并且所有的节点都尽可能地集中在左侧。
设计一个用完全二叉树初始化的数据结构 CBTInserter，它支持以下几种操作：
CBTInserter(TreeNode root) 使用根节点为 root 的给定树初始化该数据结构；
CBTInserter.insert(int v) 向树中插入一个新节点，节点类型为 TreeNode，值为 v 。使树保持完全二叉树的状态，并返回插入的新节点的父节点的值；
CBTInserter.get_root() 将返回树的根节点。
示例：
输入：inputs = [“CBTInserter”,“insert”,“get_root”], inputs = [[[1]],[2],[]]
输出：[null,1,[1,2]]

本题难点在于初始化q使得q的所有结点都是待插入结点，使用层序遍历的方法可以解决。

class CBTInserter {
public:
    queue<TreeNode*> q; 
    TreeNode* m_root;
    CBTInserter(TreeNode* root):m_root(root) {
        q.push(root);
        // 层序遍历初始化q使得q的所有结点都是待插入结点
        while (q.front()->left && q.front()->right) {
            q.push(q.front()->left);
            q.push(q.front()->right);
            q.pop();
        }
        if (q.front()->left) q.push(q.front()->left); // 有左子树就加上
    }
    
    int insert(int v) {
        int res = q.front()->val;
        if (!q.front()->left) {
            q.front()->left = new TreeNode(v);
            q.push(q.front()->left);
        }
        else {
            q.front()->right = new TreeNode(v);
            q.push(q.front()->right);
            q.pop();
        }
        return res;
    }
    
    TreeNode* get_root() {
        return m_root;
    }
};

---

剑指 Offer II 046. 二叉树的右侧视图 Medium 层序遍历 DFS 2023/3/10

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。
示例：
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

层序遍历套用队列模板，每层弹出第len-1个结点。

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        if (!root) return {};
        queue<TreeNode*> q;
        vector<int> res;
        q.push(root);
        while (!q.empty()) {
            int len = q.size();
            for (int i = 0; i < len; i++) {
                TreeNode* cur = q.front();      
                q.pop();
                if (i == len - 1) res.push_back(cur->val);
                if (cur->left) q.push(cur->left);
                if (cur->right) q.push(cur->right);
            }
        }
        return res;
    }
};

使用DFS记录当前层的深度和最大深度，并采用先右子树后左子树的遍历方式，遇到没有遍历过的深度就记录下来。

class Solution {
public:
    vector<int> res;
    int cur_depth = 0;
    int max_depth = -1;
    vector<int> rightSideView(TreeNode* root) {
        dfs(root);
        return res;
    }
    void dfs(TreeNode* root) {
        if (!root) return;
        if (cur_depth > max_depth) {
            max_depth = cur_depth;
            res.push_back(root->val);
        }
        cur_depth++;
        dfs(root->right);
        dfs(root->left);
        cur_depth--;
    }
};

---

剑指 Offer II 047. 二叉树剪枝 Medium 后序遍历 2023/3/10

给定一个二叉树 根节点 root ，树的每个节点的值要么是 0，要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。
节点 node 的子树为 node 本身，以及所有 node 的后代。
示例：
输入: [1,null,0,0,1]
输出: [1,null,0,null,1]

在后序遍历位置，找到左子树为单独的0结点和右子树为单独的0结点并删除。
这里类似链表使用了哑结点便于处理。

class Solution {
public:
    TreeNode* pruneTree(TreeNode* root) {
        TreeNode* dummy = new TreeNode(1, nullptr, root);
        dfs(dummy);
        return dummy->right;
    }
    void dfs(TreeNode* root) {
        if (!root) return;
        dfs(root->left);
        dfs(root->right);
        if (root->left && root->left->val == 0 && !root->left->left && !root->left->right)
            root->left = nullptr;
        if (root->right && root->right->val == 0 && !root->right->left && !root->right->right)
            root->right = nullptr;
    }
};

带返回值的DFS，直接在原结点上操作，遇到单独的0结点就删除。

class Solution {
public:
    TreeNode* pruneTree(TreeNode* root) {
        if (!root) return root;
        root->left = pruneTree(root->left);
        root->right = pruneTree(root->right);
        if (root->val == 0 && !root->left && !root->right) return nullptr;
        return root;
    }
};

---

剑指 Offer II 048. 序列化与反序列化二叉树 Hard 建树 2023/3/10

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。
请设计一个string serialize(TreeNode* root)方法和TreeNode* deserialize(string data)方法来实现二叉树的序列化与反序列化。

这里的序列化为字符串可以选择先序遍历和后序遍历。这里选择先序遍历建立字符串。
在反序列建树过程中，首先将字符串转为字符数组，再对其左右子树分别建树。这里使用deque容器便于首结点删除操作。

class Codec {
public:
    // 序列化为字符串
    string serialize(TreeNode* root) {
        if (!root) return "";
        string str;
        dfs(root, str);
        return str;
    }
    void dfs(TreeNode* root, string& str) {
        if (!root) str += "None,";
        else {
            // 先序遍历建立字符串
            str += to_string(root->val) + ",";
            dfs(root->left, str);
            dfs(root->right, str);
        }
    }

    // 反序列化建树
    TreeNode* deserialize(string data) {
        if (data.empty()) return nullptr;
        // 将字符串转为vector
        deque<string> res;
        string str;
        for (char c: data) {
            if (c == ',') {
                res.push_back(str);
                str.clear();
            }
            else str += c;
        }
        return helper(res);
    }
    TreeNode* helper(deque<string>& res) {
        if (res.front() == "None") {
            res.pop_front();
            return nullptr;
        }
        // 新建结点并对其左右子树分别建树
        TreeNode* root = new TreeNode(stoi(res.front()));
        res.pop_front();
        root->left = helper(res);
        root->right = helper(res);
        return root;
    }
};

---

剑指 Offer II 050. 向下的路径节点之和 Medium 前缀和 2023/3/10

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

可以对每个结点进行dfs但是这样时间复杂度为$O(n^2)$ ，可以通过前缀和降低时间复杂度到$O(n)$。
使用map容器记录当前前缀和存在的数值和出现的次数。其中++和–的操作类似回溯，对前缀和求差的前提是要保证map中所保存的前缀和均为同一路径上的结点的前缀和，因此需要删除返回前的节点所代表的前缀和。

为什么有 $prefix[0]=1?$ 这是因为任何节点本身也可以形成一个路径（长度为1的路径）。如果某个节点的值就为target，那么它本身就是一个解。前缀和0正好可以与它形成这个解。对任何节点而言，本身就是解最多只能有一个，所以一开始put(0, 1)。相当于给所有节点一个可单独形成合法路径的机会。

class Solution {
public:
    unordered_map<long long, int> prefix;
    int ret = 0;
    void dfs(TreeNode *root, long long cur, int targetSum) {
        if (!root) return;
        cur += root->val;
        // 找到路径
        if (prefix.count(cur - targetSum)) ret += prefix[cur - targetSum];
        prefix[cur]++;
        dfs(root->left, cur, targetSum);
        dfs(root->right, cur, targetSum);
        prefix[cur]--;
    }

    int pathSum(TreeNode* root, int targetSum) {
        prefix[0] = 1; // 看上面的解释
        dfs(root, 0, targetSum);
        return ret;
    }
};

---

剑指 Offer II 054. 所有大于等于节点的值之和 Medium 逆中序遍历 2023/3/11

给定一个二叉搜索树，请将它的每个节点的值替换成树中大于或者等于该节点值的所有节点值之和。

考虑到累加的顺序为8->7->6->5…->2->1，恰好为倒序，而正序为中序遍历，则使用先右后左的中序遍历。每次加上累加值并替换原值。

class Solution {
public:
    int sum = 0;
    TreeNode* convertBST(TreeNode* root) {
        if (!root) return nullptr;
        convertBST(root->right);
        root->val += sum;
        sum = root->val;
        convertBST(root->left);
        return root;
    }
};

---