R：optim()函数——回归优化案例分析

目的

使用optim()函数寻找最优的参数值，使残差平方和最小（最小二乘法）。

步骤

数据

R自带数据集Indometh，有66行、3列，分别为Subject（患者编号），time（血液样本采集时间）和conc（血液样本中indomethacine的含量）。

数学模型

$$conc=a_{1}exp(-exp(l_1)time)+a_{2}exp(-exp(l_1)time)$$
其中 $a_1$, $a_2$, $l_1$, $l_2$是要估计的参数值。

model<-function(p,t){
  # p[1] 到 p[4] 分别为4个参数 : a1, a2, l1, l2
  return(p[1]*exp(-exp(p[3])*t)+p[2]*exp(-exp(p[4])*t))
}

最小二乘法

cost<-function(p,t){
  return(sum((Indometh$conc-model(p,t))^2))
}

优化函数 optim()

初始值设定为：
$a_1=3$,
$a_2=0.6$,
$l_1=1$,
$l_2=-1.3$

使用的优化算法： BFGS （Quasi-Newton Method）

opt<-optim(c(3, 0.6, 1, -1.3), cost, method="BFGS", t=Indometh$time)
# 将参数存储在par中
par<-opt$par

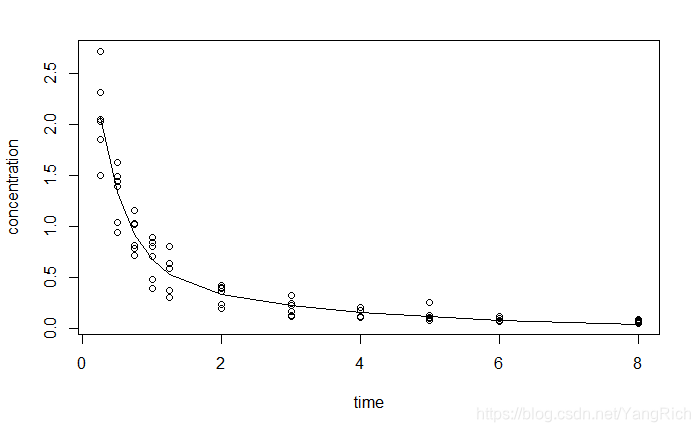
画图

plot(Indometh$time, Indometh$conc, xlab = "time", ylab = "concentration")
lines(unique(Indometh$time), model(par, unique(Indometh$time)))

实线为拟合的模型，点为实际值。