44 二叉搜索树中第K个小的元素
二叉搜索树中第K个小的元素
-
- 题解1 中序遍历
- 题解2 AVL(手撕平衡二叉树:谢谢力扣官方)
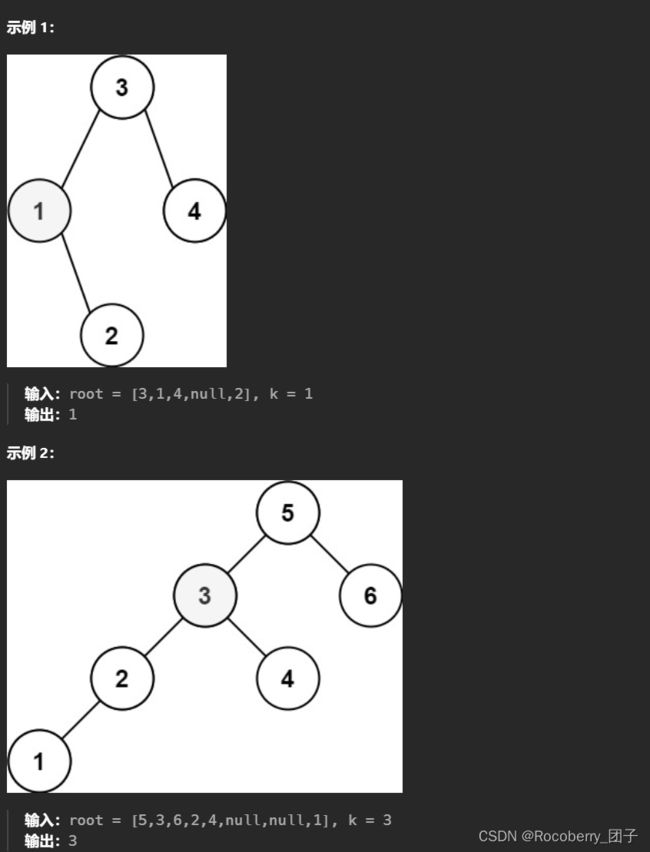
给定一个二叉搜索树的根节点
root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
- 树中的节点数为 n 。
- 1 <=
k<=n<= 1 0 4 10^4 104 - 0 <=
Node.val<= 1 0 4 10^4 104
进阶:如果二叉搜索树经常被修改(插入/删除操作)并且你需要频繁地查找第 k 小的值,你将如何优化算法?
题解1 中序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
vector<int> vals;
stack<TreeNode*> kk;
while(vals.size() < k){
while(root){
kk.push(root);
root = root->left;
}
root = kk.top();
kk.pop();
vals.emplace_back(root->val);
root = root->right;
}
return vals.back();
}
};
题解2 AVL(手撕平衡二叉树:谢谢力扣官方)
// 平衡二叉搜索树结点
struct Node {
int val;
Node * parent;
Node * left;
Node * right;
int size;
int height;
Node(int val) {
this->val = val;
this->parent = nullptr;
this->left = nullptr;
this->right = nullptr;
this->height = 0; // 结点高度:以node为根节点的子树的高度(高度定义:叶结点的高度是0)
this->size = 1; // 结点元素数:以node为根节点的子树的节点总数
}
Node(int val, Node * parent) {
this->val = val;
this->parent = parent;
this->left = nullptr;
this->right = nullptr;
this->height = 0; // 结点高度:以node为根节点的子树的高度(高度定义:叶结点的高度是0)
this->size = 1; // 结点元素数:以node为根节点的子树的节点总数
}
Node(int val, Node * parent, Node * left, Node * right) {
this->val = val;
this->parent = parent;
this->left = left;
this->right = right;
this->height = 0; // 结点高度:以node为根节点的子树的高度(高度定义:叶结点的高度是0)
this->size = 1; // 结点元素数:以node为根节点的子树的节点总数
}
};
// 平衡二叉搜索树(AVL树):允许重复值
class AVL {
public:
AVL(vector<int> & vals) {
if (!vals.empty()) {
root = build(vals, 0, vals.size() - 1, nullptr);
}
}
// 根据vals[l:r]构造平衡二叉搜索树 -> 返回根结点
Node * build(vector<int> & vals, int l, int r, Node * parent) {
int m = (l + r) >> 1;
Node * node = new Node(vals[m], parent);
if (l <= m - 1) {
node->left = build(vals, l, m - 1, node);
}
if (m + 1 <= r) {
node->right = build(vals, m + 1, r, node);
}
recompute(node);
return node;
}
// 返回二叉搜索树中第k小的元素
int kthSmallest(int k) {
Node * node = root;
while (node != nullptr) {
int left = getSize(node->left);
if (left < k - 1) {
node = node->right;
k -= left + 1;
} else if (left == k - 1) {
break;
} else {
node = node->left;
}
}
return node->val;
}
void insert(int v) {
if (root == nullptr) {
root = new Node(v);
} else {
// 计算新结点的添加位置
Node * node = subtreeSearch(root, v);
bool isAddLeft = v <= node->val; // 是否将新结点添加到node的左子结点
if (node->val == v) { // 如果值为v的结点已存在
if (node->left != nullptr) { // 值为v的结点存在左子结点,则添加到其左子树的最右侧
node = subtreeLast(node->left);
isAddLeft = false;
} else { // 值为v的结点不存在左子结点,则添加到其左子结点
isAddLeft = true;
}
}
// 添加新结点
Node * leaf = new Node(v, node);
if (isAddLeft) {
node->left = leaf;
} else {
node->right = leaf;
}
rebalance(leaf);
}
}
// 删除值为v的结点 -> 返回是否成功删除结点
bool Delete(int v) {
if (root == nullptr) {
return false;
}
Node * node = subtreeSearch(root, v);
if (node->val != v) { // 没有找到需要删除的结点
return false;
}
// 处理当前结点既有左子树也有右子树的情况
// 若左子树比右子树高度低,则将当前结点替换为右子树最左侧的结点,并移除右子树最左侧的结点
// 若右子树比左子树高度低,则将当前结点替换为左子树最右侧的结点,并移除左子树最右侧的结点
if (node->left != nullptr && node->right != nullptr) {
Node * replacement = nullptr;
if (node->left->height <= node->right->height) {
replacement = subtreeFirst(node->right);
} else {
replacement = subtreeLast(node->left);
}
node->val = replacement->val;
node = replacement;
}
Node * parent = node->parent;
Delete(node);
rebalance(parent);
return true;
}
private:
Node * root;
// 删除结点p并用它的子结点代替它,结点p至多只能有1个子结点
void Delete(Node * node) {
if (node->left != nullptr && node->right != nullptr) {
return;
// throw new Exception("Node has two children");
}
Node * child = node->left != nullptr ? node->left : node->right;
if (child != nullptr) {
child->parent = node->parent;
}
if (node == root) {
root = child;
} else {
Node * parent = node->parent;
if (node == parent->left) {
parent->left = child;
} else {
parent->right = child;
}
}
node->parent = node;
}
// 在以node为根结点的子树中搜索值为v的结点,如果没有值为v的结点,则返回值为v的结点应该在的位置的父结点
Node * subtreeSearch(Node * node, int v) {
if (node->val < v && node->right != nullptr) {
return subtreeSearch(node->right, v);
} else if (node->val > v && node->left != nullptr) {
return subtreeSearch(node->left, v);
} else {
return node;
}
}
// 重新计算node结点的高度和元素数
void recompute(Node * node) {
node->height = 1 + max(getHeight(node->left), getHeight(node->right));
node->size = 1 + getSize(node->left) + getSize(node->right);
}
// 从node结点开始(含node结点)逐个向上重新平衡二叉树,并更新结点高度和元素数
void rebalance(Node * node) {
while (node != nullptr) {
int oldHeight = node->height, oldSize = node->size;
if (!isBalanced(node)) {
node = restructure(tallGrandchild(node));
recompute(node->left);
recompute(node->right);
}
recompute(node);
if (node->height == oldHeight && node->size == oldSize) {
node = nullptr; // 如果结点高度和元素数都没有变化则不需要再继续向上调整
} else {
node = node->parent;
}
}
}
// 判断node结点是否平衡
bool isBalanced(Node * node) {
return abs(getHeight(node->left) - getHeight(node->right)) <= 1;
}
// 获取node结点更高的子树
Node * tallChild(Node * node) {
if (getHeight(node->left) > getHeight(node->right)) {
return node->left;
} else {
return node->right;
}
}
// 获取node结点更高的子树中的更高的子树
Node * tallGrandchild(Node * node) {
Node * child = tallChild(node);
return tallChild(child);
}
// 重新连接父结点和子结点(子结点允许为空)
static void relink(Node * parent, Node * child, bool isLeft) {
if (isLeft) {
parent->left = child;
} else {
parent->right = child;
}
if (child != nullptr) {
child->parent = parent;
}
}
// 旋转操作
void rotate(Node * node) {
Node * parent = node->parent;
Node * grandparent = parent->parent;
if (grandparent == nullptr) {
root = node;
node->parent = nullptr;
} else {
relink(grandparent, node, parent == grandparent->left);
}
if (node == parent->left) {
relink(parent, node->right, true);
relink(node, parent, false);
} else {
relink(parent, node->left, false);
relink(node, parent, true);
}
}
// trinode操作
Node * restructure(Node * node) {
Node * parent = node->parent;
Node * grandparent = parent->parent;
if ((node == parent->right) == (parent == grandparent->right)) { // 处理需要一次旋转的情况
rotate(parent);
return parent;
} else { // 处理需要两次旋转的情况:第1次旋转后即成为需要一次旋转的情况
rotate(node);
rotate(node);
return node;
}
}
// 返回以node为根结点的子树的第1个元素
static Node * subtreeFirst(Node * node) {
while (node->left != nullptr) {
node = node->left;
}
return node;
}
// 返回以node为根结点的子树的最后1个元素
static Node * subtreeLast(Node * node) {
while (node->right != nullptr) {
node = node->right;
}
return node;
}
// 获取以node为根结点的子树的高度
static int getHeight(Node * node) {
return node != nullptr ? node->height : 0;
}
// 获取以node为根结点的子树的结点数
static int getSize(Node * node) {
return node != nullptr ? node->size : 0;
}
};
class Solution {
public:
int kthSmallest(TreeNode * root, int k) {
// 中序遍历生成数值列表
vector<int> inorderList;
inorder(root, inorderList);
// 构造平衡二叉搜索树
AVL avl(inorderList);
// 模拟1000次插入和删除操作
vector<int> randomNums(1000);
std::random_device rd;
for (int i = 0; i < 1000; ++i) {
randomNums[i] = rd()%(10001);
avl.insert(randomNums[i]);
}
shuffle(randomNums); // 列表乱序
for (int i = 0; i < 1000; ++i) {
avl.Delete(randomNums[i]);
}
return avl.kthSmallest(k);
}
private:
void inorder(TreeNode * node, vector<int> & inorderList) {
if (node->left != nullptr) {
inorder(node->left, inorderList);
}
inorderList.push_back(node->val);
if (node->right != nullptr) {
inorder(node->right, inorderList);
}
}
void shuffle(vector<int> & arr) {
std::random_device rd;
int length = arr.size();
for (int i = 0; i < length; i++) {
int randIndex = rd()%length;
swap(arr[i],arr[randIndex]);
}
}
};