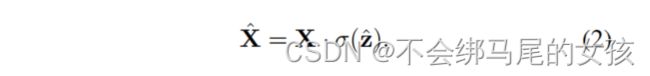Coordinate attention,SE,CBAM
1、SE
因为普通卷积难以建模信道关系,SE考虑通道的相互依赖关系增强模型对信息通道的敏感性,同时全局平均池化可以帮助模型捕获全局信息。然而SE只考虑了内部通道信息而忽略了位置信息的重要性。
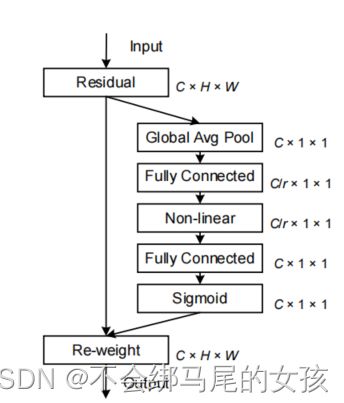
输入X首先经过全局平均池化
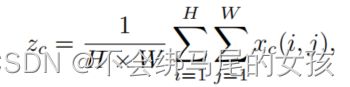
然后经过全连接层来捕获每个通道的重要性,再经过非线性层也就是使用ReLU激活函数来增加非线性因素,再经过全连接层来捕获每个通道的重要性。
最后全连接层的输出用sigmoid归一化加权后和输入X通道乘法。
2、CA(coordinate attention)

主要分为两步,位置信息的嵌入和协调注意力生成。
(1)位置信息嵌入:
全局平均池化通常用于通道注意中,它将全局位置信息压缩到通道信息中,很难保持位置信息。所在我们通过两个维度上的一维平均池化,这种转换允许获得该方向上的长期依赖关系和保持另一方向上的位置信息,有助于网络更加精准地定位感兴趣的对象。
给定输入x,我们使用(H,1)或(1,W)分别沿着水平坐标和垂直坐标对每个通道进行编码。


(2)协调注意力产生
沿着空间维度进行concat,然后二维卷积减少通道数,较小模型的复杂度,接着进行正则化BatchNorm和非线性激活

f沿着空间维度分成两个张量(c/r,1,H)和(c/r,1,w),然后分别经过卷积恢复到和输入x相同的通道数,最后经过sigmoid归一化加权。
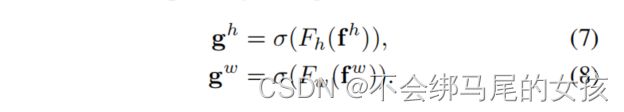
协调注意力Y的输出可以表达成公式9,相当于将gh和gw作为注意力权重来使用。沿着水平方向和垂直方向的注意同时应用于输入张量,这两个注意力图中的每个元素都反映了感兴趣的对象是否存在于相对于的队和列中。
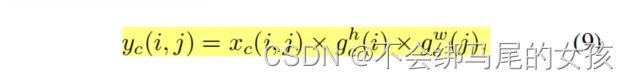
CA中,两个一维的全局池化操作,使得网络可以获得更大的一个感受野以及编码准确的空间位置信息。CA考虑了不同通道之间关系的重要性同时也考虑了编码空间信息。
3、CBAM
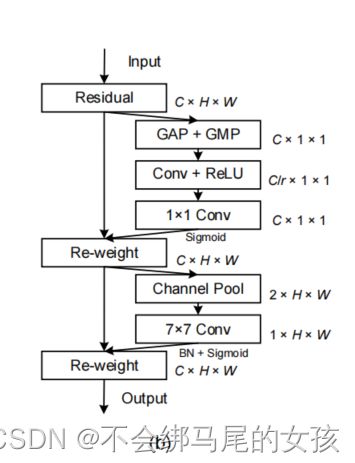
首先,CBAM使用squeeze通道数到1导致信息损失。然而在CA中使用适当的较少比率r来缩减通道数,避免过多的通道信息的丢失。
其次,CBAM使用7x7卷积来获得局部空间位置信息,而CA是通过两个一维全局池化,使得可以捕获到空间位置之间的长期依赖关系。
CBAM是通过对每个位置的多个通道取最大值和平均值来作为加权系数,这种加权只考虑局部范围的信息。
4、CA代码
大佬写的代码,先记录在这里,方便后期复习回顾方便。
import torch
import torch.nn as nn
#---------------------------------------------------#
#CA模块这个类的定义
#其参数共有三个分别为特征图像的高、宽以及通道数
#在经过CA模块的前后,特征图像的通道数并不会发生变化
#使用池化不会造成数据矩阵深度的改变,只会在高度和宽带上降低,达到降维的目的
#池化并不会改变特征图像的通道数
#---------------------------------------------------#
class CA_Block(nn.Module):
def __init__(self, channels,reduction=16):
super(CA_Block, self).__init__()
self.avg_pool_x = nn.AdaptiveAvgPool2d((None, 1)) # 先后顺序为h,w 为1则为在x轴进行平均池化操作,x轴即为水平方向w,进而使w的值变为1
self.avg_pool_y = nn.AdaptiveAvgPool2d((1, None)) #在y轴进行平均池化操作,y轴为垂直方向h,进而使h的值变为1
self.conv_1x1 = nn.Conv2d(in_channels=channels, out_channels=channels // reduction, kernel_size=1, stride=1,
bias=False) #图中的r即为reduction,进而使其输出的特征图像的通道数变为原先的1/16
self.relu = nn.ReLU() #relu激活函数
self.bn = nn.BatchNorm2d(channels // reduction) #二维的正则化操作
self.F_h = nn.Conv2d(in_channels=channels // reduction, out_channels=channels, kernel_size=1, stride=1,
bias=False) #将垂直方向上的通道数通过卷积来将其复原
self.F_w = nn.Conv2d(in_channels=channels // reduction, out_channels=channels, kernel_size=1, stride=1,
bias=False) #将水平方向上的通道数通过卷积来将其复原
self.sigmoid_h = nn.Sigmoid() #定义的sigmoid方法
self.sigmoid_w = nn.Sigmoid()
def forward(self, x): #定义Tensor: 16,1024,13,13
h=x.shape[2] #13
w=x.shape[3] #13
x_h = self.avg_pool_x(x).permute(0, 1, 3, 2) # 16,1024,13,1 ->16,1024,1,13
x_w = self.avg_pool_y(x) #16,1024,1,13
#现在x_h以及x_w的shape均为16,1024,1,13 两个16,1024,1,13 堆叠->16,1024,1,26 经过conv之后,成为16,64(1024/16),1,26 过BN以及ReLU进行位置信息编码
x_cat_conv_relu = self.relu(self.bn(self.conv_1x1(torch.cat((x_h, x_w), 3))))
print(x_cat_conv_relu.shape) #16,64,1,26 #具体的即为将维度3上的13与13相加,同时通过卷积调整其通道数为64,过BN以及ReLU进行位置信息编码
x_cat_conv_split_h, x_cat_conv_split_w = x_cat_conv_relu.split([h,w], 3) #按照维度3以及h和w的值将这个张量分开
#print(x_cat_conv_split_h.shape) #对于垂直方向,其输出的shape仍为16,64,1,13
#print(x_cat_conv_split_w.shape) #对于水平方向,其输出的shape仍为16,64,1,13
s_h = self.sigmoid_h(self.F_h(x_cat_conv_split_h.permute(0, 1, 3, 2))) #对于垂直方向的,为先进行一个转置,之后通过卷积达到所原先的通道数,再过sigmoid进行归一化处理
#print(s_h.shape) #为16,1024,13,1 #此为垂直方向 #16,64,1,13->16,64,13,1->conv->16,1024,13,1
s_w = self.sigmoid_w(self.F_w(x_cat_conv_split_w)) #对于水平方向,使用卷积来达到原先的通道数,之后进行归一化的处理
#print(s_w.shape) #为16,1024,1,13 #此为水平方向 16,64,1,13->conv->16,1024,1,13
out = x * (s_h.expand_as(x) * s_w.expand_as(x))# 生成attention map之后进行加权
return out
F=torch.randn(16,1024,13,13)
print('As Begin!!')
print(F.shape)
CA=CA_Block(1024)
F=CA(F)
print('After Change!!')
print(F.shape)