【算法方法-动态规划3】经典动态规划刷题--背包/贪心/其它DP问题
基于上一篇文章 子序列刷题+第一篇的框架;
进阶 大厂爱考的经典动规问题。
看+敲:一系列经典问题: 【背包问题】 【贪心类型问题】 【其它经典问题】
#2.10 2.11—— 【进阶问题…】 #2.18 2.19——答疑【动态规划和回溯到底谁是王道】
一、背包问题
1.1 0-1背包问题
我的解法
class Solution{
public:
/**
* @Description: dong's Solution:DP定义:dp[i][w]:前i个背包 承重w,所能获得的最大价值。
* @param {int} W
* @param {int} N
* @param {vector} &wt
* @return {*}
* @notes:
*/
int knapsack(int W, int N, vector<int>& wt, vector<int>& val){
// base
vector<vector<int>> dp(N+1, vector<int>(W+1, 0));
for(int i = 1; i <= N ;i++){
for(int w = 1; w <= W ;w++){
// 放入与不放入两个类别;但是 要防止装不进去
if(w - wt[i-1] < 0){
// 放不进去
dp[i][w] = dp[i-1][w];
}else{
// 可以放进去,但是看放不放找最大 价值
dp[i][w] = max(dp[i-1][w],
dp[i-1][w-wt[i-1]]+val[i-1]);
}
}
}
return dp[N][W];
}
/**
* @Description: 我的解法DP对应不同的定义:dp[i][j]: 在限定条件下 i--j所能承载的最大价值。
* @param {int} W
* @param {int} N
* @return {*}
* @notes: 关键要限定好重量 别超载;( 其次数量N已经限定了, 且题目说是N个物品 都可以遍历到。)
*/
int knapsack(int W, int N, vector<int>& wt, vector<int>& val){
// init
// first 重量,second 价值
vector<vector<pair<int, int>>> dp(N, vector<pair<int, int>>(N, pair<int,int>(0,0)));
// base: i == j时 价值为不超重的本身
// 且 遍历只遍历上三角
for(int i = 0; i < N ;i++){
if(wt[i] <= W){
// 未超载
dp[i][i].first = wt[i];
dp[i][i].second = val[i];
}
}
// dp start: 下到上 左到右
for(int i = N-2; i >= 0 ;i--){
for(int j = i+1; j < N ;j++){
// 控制 wt不超载
// i+1,j-1 归纳i,j
if(wt[i]+wt[j]+dp[i+1][j-1].first <= W){
dp[i][j].first = dp[i+1][j-1].first + wt[i] + wt[j];
dp[i][j].second = dp[i+1][j-1].second + val[i] + val[j];
}else
{ // 超载,取两者最大价值的一个。
dp[i][j] = dp[i][j-1].second> dp[i+1][j].second ?dp[i][j-1]:dp[i+1][j];
}
}
}
return dp[N][W].second;
}
};
1.2 子集背包问题(填满等于)–01背包变体
我的解法
/* @Description : 分割等和子集。
* 416. 分割等和子集
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
注意:
每个数组中的元素不会超过 100
数组的大小不会超过 200
示例 1:
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].
示例 2:
输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.
*/
#include
// dp[0][j] = false;
// }
// dp start
for(int i = 1; i <= n ;i++){
for(int j = 1; j <= w ;j++){
// 放入与不放入两个类别;但是 要防止装不进去
if(j - nums[i-1] < 0){
// 放不进去
dp[i][j] = dp[i-1][j];
}else{
// 可以放进去;取决于状态 dp[i-1][j-nums[i-1]] 或者也可以不放进去 or
dp[i][j] = dp[i-1][j-nums[i-1]] || dp[i-1][j];
}
}
}
return dp[n][w];
}
/**
* @Description: 优化状态压缩。
* @param {*}
* @return {*}
* @notes: // 状态压缩重点注意:此处防止上一行被覆盖/以至于重复使用 数值。
*/
bool canPartition(vector<int>& nums) {
// 加和
int sum=0, n=nums.size();
for(int i = 0;i<nums.size();i++){
sum+=nums[i];
}
if(sum % 2 != 0){
return false;
}
int w = sum/2;
// base
vector<bool> dp(w+1, false);
dp[0] = true;
// dp start
for(int i = 1; i <= n ;i++){
for(int j = 1; j <= w ;j++){ // 状态压缩重点注意:此处防止上一行被覆盖/以至于重复使用 数值。
if(j - nums[i-1] >= 0 ){
dp[j] = dp[j-nums[i-1]] || dp[j];
}
}
}
return dp[w];
}
};
1.3 完全背包问题
我的题解
/** @Description : 零钱兑换2
* 518. 零钱兑换 II
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。
示例 3:
输入: amount = 10, coins = [10]
输出: 1
*/
#include 二、贪心类问题
2.1 贪心算法之区间调度问题
什么是贪心算法呢?贪心算法可以认为是动态规划算法的一个特例,相比动态规划,使用贪心算法需要满足更多的条件(贪心选择性质),但是效率比动态规划要高。
比如说一个算法问题使用暴力解法需要指数级时间,如果能使用动态规划消除重叠子问题,就可以降到多项式级别的时间,如果满足贪心选择性质,那么可以进一步降低时间复杂度,达到线性级别的。
什么是**贪心选择性质呢,简单说就是:每一步都做出一个局部最优的选择,最终的结果就是全局最优。**注意哦,这是一种特殊性质,其实只有一小部分问题拥有这个性质。
比如你面前放着 100 张人民币,你只能拿十张,怎么才能拿最多的面额?显然每次选择剩下钞票中面值最大的一张,最后你的选择一定是最优的。
然而,大部分问题都明显不具有贪心选择性质。比如打斗地主,对手出对儿三,按照贪心策略,你应该出尽可能小的牌刚好压制住对方,但现实情况我们甚至可能会出王炸。这种情况就不能用贪心算法,而得使用动态规划解决,参见前文 动态规划解决博弈问题。
一、问题概述
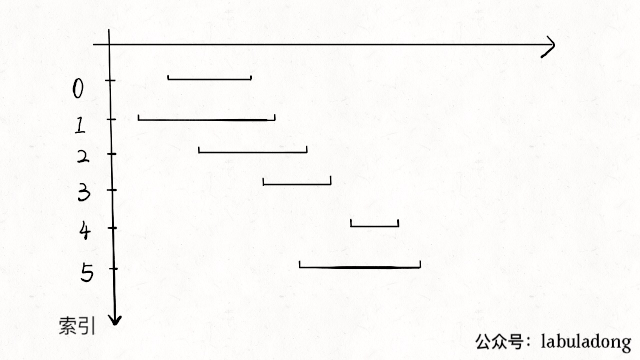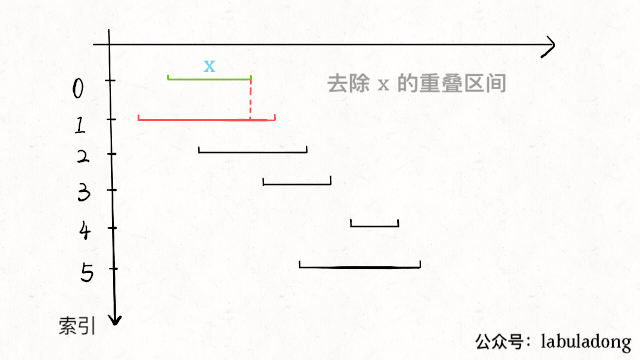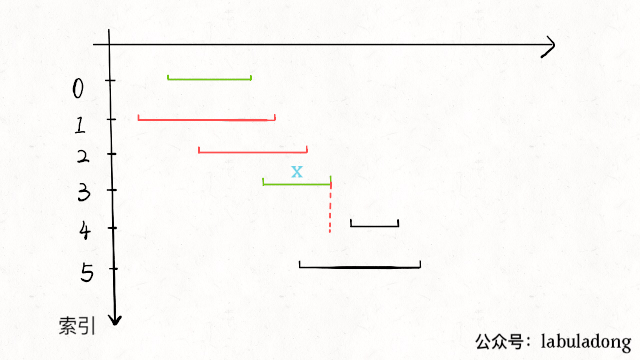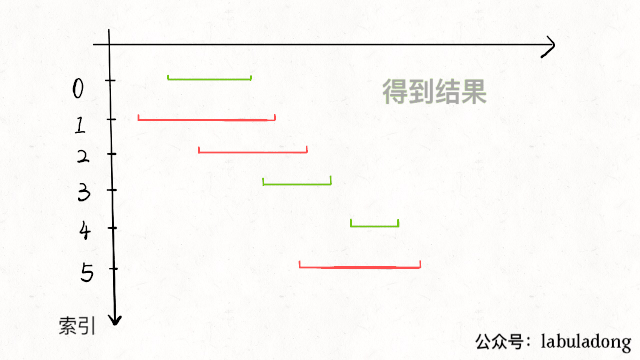
言归正传,本文解决一个很经典的贪心算法问题 Interval Scheduling(区间调度问题)。给你很多形如[start,end]的闭区间,请你设计一个算法,算出这些区间中最多有几个互不相交的区间。
int intervalScheduling(int[][] ints) {}
举个例子,intvs=[[1,3],[2,4],[3,6]],这些区间最多有两个区间互不相交,即[[1,3],[3,6]],你的算法应该返回 2。注意边界相同并不算相交。
这个问题在生活中的应用广泛,比如你今天有好几个活动,每个活动都可以用区间[start,end]表示开始和结束的时间,请问你今天最多能参加几个活动呢?
二、贪心解法
这个问题有许多看起来不错的解决思路,实际上都不能得到正确答案。比如说:
也许我们可以每次选择可选区间中开始最早的那个?但是可能存在某些区间开始很早,但是很长,使得我们错误地错过了一些短的区间。
或者我们每次选择可选区间中最短的那个?或者选择出现冲突最少的那个区间?这些方案都能很容易举出反例,不是正确的方案。
正确的思路其实很简单,可以分为以下三步:
-
从区间集合 intvs 中选择一个区间 x,这个 x 是在当前所有区间中结束最早的(end 最小)。
-
把所有与 x 区间相交的区间从区间集合 intvs 中删除。
-
重复步骤 1 和 2,直到 intvs 为空为止。之前选出的那些 x 就是最大不相交子集。
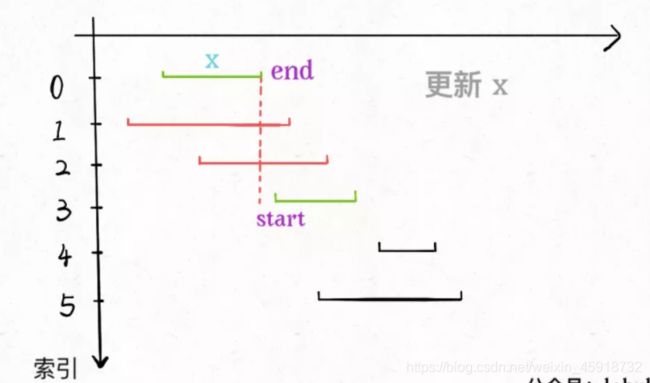
把这个思路实现成算法的话,可以按每个区间的end数值升序排序,因为这样处理之后实现步骤 1 和步骤 2 都方便很多:
现在来实现算法,对于步骤 1,由于我们预先按照end排了序,所以选择 x 是很容易的。关键在于,如何去除与 x 相交的区间,选择下一轮循环的 x 呢?
由于我们事先排了序,不难发现所有与 x 相交的区间必然会与 x 的end相交;如果一个区间不想与 x 的end相交,它的start必须要大于(或等于)x 的end:
下面看下代码:
三、应用举例
下面举例几道 LeetCode 题目应用一下区间调度算法。
2.1.1 第 435 题,无重叠区间:
我们已经会求最多有几个区间不会重叠了,那么剩下的不就是至少需要去除的区间吗?
int eraseOverlapIntervals(int[][] intervals) {
int n = intervals.length;
return n - intervalSchedule(intervals);
}
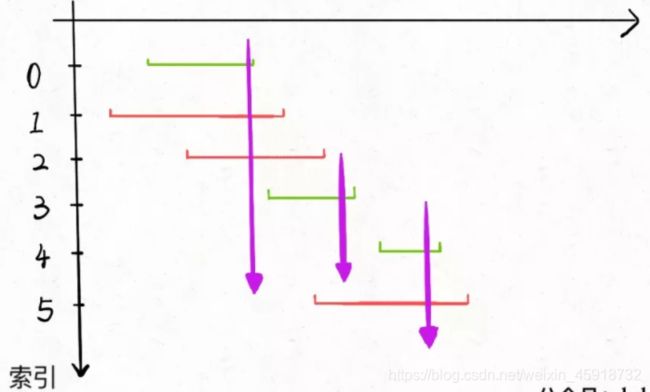
2.1.2 第 452 题,用最少的箭头射爆气球:
其实稍微思考一下,这个问题和区间调度算法一模一样!如果最多有n个不重叠的区间,那么就至少需要n个箭头穿透所有区间:
只是有一点不一样,在intervalSchedule算法中,如果两个区间的边界触碰,不算重叠;而按照这道题目的描述,箭头如果碰到气球的边界气球也会爆炸,所以说相当于区间的边界触碰也算重叠:
所以只要将之前的算法稍作修改,就是这道题目的答案:
int findMinArrowShots(int[][] intvs) {
// ...
for (int[] interval : intvs) {
int start = interval[0];
// 把 >= 改成 > 就行了
if (start > x_end) {
count++;
x_end = interval[1];
}
}
return count;
}
这么做的原因也不难理解,因为现在边界接触也算重叠,所以start == x_end时不能更新区间 x。
本文终。**对于区间问题的处理,一般来说第一步都是排序,相当于预处理降低后续操作难度。**但是对于不同的问题,排序的方式可能不同,这个需要归纳总结,以后再写写这方面的文章。
2.2 经典贪心算法–跳跃游戏
动态规划和贪心算法到底有啥关系?
说白了,贪心算法可以理解为一种特殊的动态规划问题,拥有一些更特殊的性质,可以进一步降低动态规划算法的时间复杂度。那么这一节文章,就讲 LeetCode 上两道经典的贪心算法:跳跃游戏 I 和跳跃游戏 II。
这两道题可以使用动态规划或者算法和贪心算法进行求解,通过实践,你就能更深刻地理解贪心和动规的区别和联系了。
2.2.1 Jump Game I
跳跃游戏 I 是 LeetCode 第 55 题,难度是 Medium,但实际上是比较简单的,看题目:
不知道读者有没有发现,有关动态规划的问题,大多是让你求最值的,比如最长子序列,最小编辑距离,最长公共子串等等等。这就是规律,因为动态规划本身就是运筹学里的一种求最值的算法。
那么贪心算法作为特殊的动态规划也是一样,一般也是让你求个最值。这道题表面上不是求最值,但是可以改一改:
请问通过题目中的跳跃规则,最多能跳多远?如果能够越过最后一格,返回 true,否则返回 false。
所以说,这道题肯定可以用动态规划求解的。但是由于它比较简单,下一道题再用动态规划和贪心思路进行对比,现在直接上贪心的思路:
bool canJump(vector<int>& nums) {
int n = nums.size();
int farthest = 0;
for (int i = 0; i < n - 1; i++) {
// 不断计算能跳到的最远距离
farthest = max(farthest, i + nums[i]);
// 可能碰到了 0,卡住跳不动了
if (farthest <= i) return false;
}
return farthest >= n - 1;
}
你别说,如果之前没有做过类似的题目,还真不一定能够想出来这个解法。每一步都计算一下从当前位置最远能够跳到哪里,然后和一个全局最优的最远位置farthest做对比,通过每一步的最优解,更新全局最优解,这就是贪心。
很简单是吧?记住这一题的思路,看第二题,你就发现事情没有这么简单。。。
2.2.2 Jump Game II
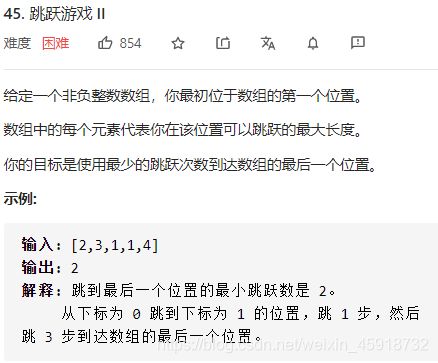
这是 LeetCode 第 45 题,也是让你在数组上跳,不过难度是 Hard,解法比上一题困难一些:
现在的问题是,保证你一定可以跳到最后一格,请问你最少要跳多少次,才能跳过去?
我们先来说说动态规划的思路,采用自顶向下的递归动态规划,可以这样定义一个dp函数:
// 定义:从索引 p 跳到最后一格,至少需要 dp(nums, p) 步
int dp(vector<int>& nums, int p);
我们想求的结果就是dp(nums, 0),base case 就是当p超过最后一格时,不需要跳跃:
if (p >= nums.size() - 1) {
return 0;
}
根据前文 动态规划套路详解 的动规框架,就可以暴力穷举所有可能的跳法,通过备忘录memo消除重叠子问题,取其中的最小值最为最终答案:
vector<int> memo;
// 主函数
int jump(vector<int>& nums) {
int n = nums.size();
// 备忘录都初始化为 n,相当于 INT_MAX
// 因为从 0 调到 n - 1 最多 n - 1 步
memo = vector<int>(n, n);
return dp(nums, 0);
}
int dp(vector<int>& nums, int p) {
int n = nums.size();
// base case
if (p >= n - 1) {
return 0;
}
// 子问题已经计算过
if (memo[p] != n) {
return memo[p];
}
int steps = nums[p];
// 你可以选择跳 1 步,2 步...
for (int i = 1; i <= steps; i++) {
// 穷举每一个选择
// 计算每一个子问题的结果
int subProblem = dp(nums, p + i);
// 取其中最小的作为最终结果
memo[p] = min(memo[p], subProblem + 1);
}
return memo[p];
}
这个动态规划应该很明显了,按照 动态规划套路详解 所说的套路,状态就是当前所站立的索引p,选择就是可以跳出的步数。
该算法的时间复杂度是 递归深度 × 每次递归需要的时间复杂度**,即 O(N^2),在 LeetCode 上是无法通过所有用例的,会超时。**
**贪心算法比动态规划多了一个性质:贪心选择性质。**我知道大家都不喜欢看严谨但枯燥的数学形式定义,那么我们就来直观地看一看什么样的问题满足贪心选择性质。
刚才的动态规划思路,不是要穷举所有子问题,然后取其中最小的作为结果吗?核心的代码框架是这样:
int steps = nums[p];
// 你可以选择跳 1 步,2 步...
for (int i = 1; i <= steps; i++) {
// 计算每一个子问题的结果
int subProblem = dp(nums, p + i);
res = min(subProblem + 1, res);
}
for 循环中会陷入递归计算子问题,这是动态规划时间复杂度高的根本原因。
但是,真的需要「递归地」计算出每一个子问题的结果,然后求最值吗?直观地想一想,似乎不需要递归,只需要判断哪一个选择最具有「潜力」即可:
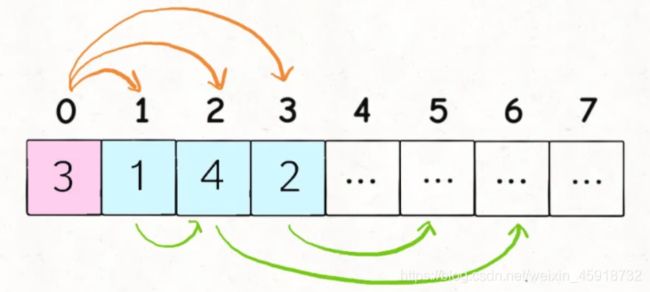
比如上图这种情况应该跳多少呢?
**显然应该跳 2 步调到索引 2,因为nums[2]的可跳跃区域涵盖了索引区间[3…6],比其他的都大。**如果想求最少的跳跃次数,那么往索引 2 跳必然是最优的选择。
你看,这就是贪心选择性质,我们不需要「递归地」计算出所有选择的具体结果然后比较求最值,而只需要做出那个最有「潜力」,看起来最优的选择即可。 【重点!!!!】
绕过这个弯儿来,就可以写代码了:
int jump(vector<int>& nums) {
int n = nums.size();
int end = 0, farthest = 0;
int jumps = 0;
for (int i = 0; i < n - 1; i++) {
farthest = max(nums[i] + i, farthest);
if (end == i) {
jumps++;
end = farthest;
}
}
return jumps;
}
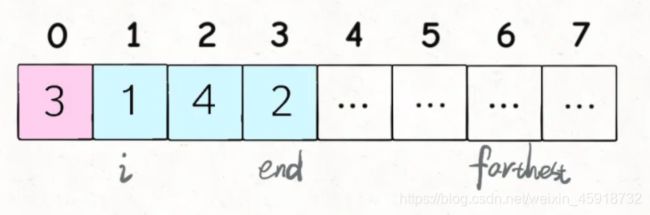
结合刚才那个图,就知道这段短小精悍的代码在干什么了:
i和end标记了可以选择的跳跃步数,farthest标记了所有可选择跳跃步数[i…end]中能够跳到的最远距离,jumps记录了跳跃次数。
本算法的时间复杂度 O(N),空间复杂度 O(1),可以说是非常高效,动态规划都被吊起来打了。
至此,两道跳跃问题都使用贪心算法解决了。
其实对于贪心选择性质,是可以有严格的数学证明的,有兴趣的读者可以参看《算法导论》第十六章,专门有一个章节介绍贪心算法。这里限于篇幅和通俗性,就不展开了。
使用贪心算法的实际应用还挺多,比如赫夫曼编码也是一个经典的贪心算法应用。更多时候运用贪心算法可能不是求最优解,而是求次优解以节约时间,比如经典的旅行商问题。
不过我们常见的贪心算法题目,就像本文的题目,大多一眼就能看出来,大不了就先用动态规划求解,如果动态规划都超时,说明该问题存在贪心选择性质无疑了。 【重点!!】
三、其它经典问题
见下一篇文章:XXX。