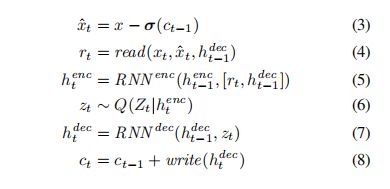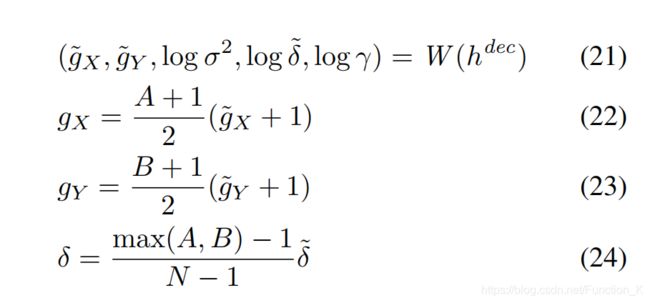论文笔记与解读《DRAW: A Recurrent Neural Network for Image Generation》

前言

笔者临近硕士毕业，我的硕士毕业项目十分类似一个非常著名的研究工作： DRAW: A Recurrent Neural Network for Image Generation，该项工作由2015年由Google Deepmind发表在ICML并产生了很大的影响力。其核心贡献点在于，通过视觉注意力关注区域序列，并基于变分自动编码器Variational AutoEncoder (VAEs)，对图像进行生成，而不是将整张图象送入神经网络中进行压缩。

1. 摘要

本文介绍了深度递归书写器（DRAW）神经网络用于图像生成。 DRAW网络是一种模仿人眼空间注意力机制的带有视觉偏好性的，
可变自动编码框架，其主要功能是用于复杂图像的迭代构造。该系统对MNIST上的生成模型的最新技术进行了大幅改善。同时，在街景门牌号码数据集上进行训练，模型生成的图像无法用肉眼与真实数据区分开。

2. 简介与Motivation

 深度递归注意力作家(DRAW)体系结构代表了一种向更自然的图像构造形式的转变，其中场景的部分是独立于其他场景和应用程序创建的，近似草图被依次细化。这个研究工作的motivation是当我们人类在被要求进行绘画和回忆场景的时候，我们通常是以序列的方式进行回顾的。人类在观察图像的过程中，通常每次只观测一小部分，这是因为人类的视觉带宽是有限的。同时，在潜在的视觉注意力机制引导下，通过对全图进行扫描，我们最终可以对原始场景进行回忆和重构，这样一个过程是十分自然，干净，优雅的。

那么如何实现这样的一种机制呢？答案是通过一组RNN网络构成的变分自动编码器进行实现：一个编码器网络用来对真实图像进行压缩，同时一个解码器对压缩后图像进行恢复。二者的组合完全是一个端到端的SGD过程，这里的损失函数是一个二进制交叉熵和KL散度。与众不同的是，模型生成的过程不是一次single pass的方式，而是一种迭代重建的方式，通过修改decoder的预测结果来不断地对最终结果进行累计。

3. DRAW网络模型

基本的DRAW模型结构与传统的变分编码器结构相类似，它是由一组编码器和解码器网络构成的。其中编码器是决定了潜在变量空间的分布用来捕捉显著的输入信息；一个解码器用来接受从编码分布中采样出出来的样本，并使用它们对图像上的自身分布进行条件化。

然而这里有三个关键的不同点：

1. DRAW结构中的编码器和解码器的结构都是Recurrent Neural Network，也就是说它处理的输入是一个时间序列的数据，这意味着编码空间的样本序列是时刻在他们中间进行交换的。
2. 对于解码器来说，编码器的先前输出状态是私密的，不共享的。这意味着编码器的行为，是根据到目前为止的解码器的行为造成的。其次，解码器的输出是不断被添加到最终的分布，从而修改生成的数据，而不是在一步中输出全部的数据
3. 一个动态更新的注意力机制被使用，用于同时限制输编码器的观测点和解码器的输出区域

简单而言，是由网络决定“每步看哪”然后同时决定“写哪”和“写什么”。神经结构图如下所示：

如图所示，左边是传统的变分编码器流程。输入x进入编码器，同时生成潜在的编码空间后进行Q sampling过程得到Q(z|x)，并将采样结果作为潜在编码空间z交给解码器，解码器再根据z的条件生成对应的分布P(x|z) 作为自动编码器的输出。 右边是本文提出的网络结构。其基本流程如下：

基本组成部分：输入数据x，read操作，RNN编码器，Q采样，RNN解码器，write操作。

基本过程（以t时刻状态为准）：

1. t状态一个batch的输入数据x；上一个t-1状态的编码器输出，以及t-1状态解码器的输出c(t-1)；送入t时刻的read
2. read后将结果送入RNN编码器，同时将t-1状态的编码器输出，上个状态的解码器输出；送入t时刻的RNN编码器
3. t时刻的编码器输出进行Q采样，该输出为当前时刻的z潜在空间
4. 将隐藏空间的z送入解码器，同时将t-1状态的解码器输出送入解码器RNN；获得t时刻解码器输出
5. 将t时刻的解码输出，和t-1状态的临时结果c(t-1)，送入t时刻的write操作，并产生临时结果c(t) 保存在canvas matrix中
6. 循环当前过程进入t+1时间状态，循环到t循环了整个过程，产生最终结果。

网络结构和计算拓扑关系的设计：

网络的基本结构和数据流如上所述，需要强调的是这里的RNN可以采用任何形式的RNN网络。同时隐藏空间变量是一个对角高斯分布。然而，高斯潜函数的一个很大的优点是，可以使用所谓的重新参数化技巧 (reparameterization trick)，轻松地获得样本函数相对于分布参数的梯度。这样的操作能够使得使用潜在分布的，前向反向传递的过程是无偏的，低方差的，使得随机梯度更容易操作。

因为我们的出发点是模拟人类视觉，那么假设我们观察一张图像存在T个状态，那么我们的过程应该循环遍历这T个状态，同时让网络在T个状态中不断获取数据，共享权重信息，来达成我们的预期期望。那么在1...T个时间状态中，共分为以下几个步骤：

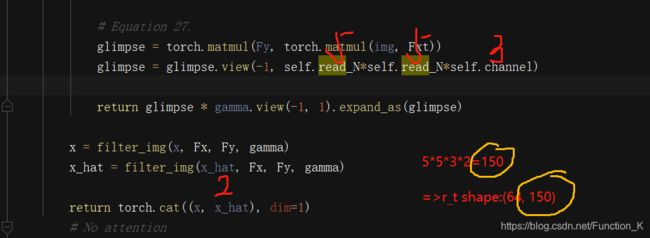
第一步是计算误差图像，通过上一个状态的c(t-1)，经过激活函数（这里我们使用的是sigmoid function）后，用原始输入图像减去它，得到error image，这就是第一步。第二步，就是将当前t时刻状态的输入xt和error image xt hat，以及上一个t-1状态的解码器输出送入read操作，得到的是read后，glimpse的结果。具体的read操作的实现，在本文后续进行讲解。这里我们看一下Debug出来的r_t的结果。

可以看出r_t这时候的shape是(64, 150)，这是因为我们在最初glimpse的数量设计的参数问题。这里简单解释以下，通过这个截图，读者应该能够明白这其中的道理，因此我们就不多做阐述了。具体的read与write的实现，我们在本文的后半部分进行讲解。这里需要注意到的一点是，在本文中，虽然作者题出编码器的状况可以作为输入递给read，但是对模型的performance没有什么太大影响，所以我们没有使用这个操作。

那么到此，DRAW的网络结构和计算方式我们已经基本解释完毕。

4. 损失函数的设计

最终的画布矩阵cT是被用于参数化输入数据的。如果输入是二进制的，那么D是伯努利分布，同时它的平均值是cT的sigmoid激活值。那么重构损失Lx是D(x|cT)的负对数概率：

第二个损失是隐藏空间的损失，这部分损失是对序列的潜在分布计算的，是他对应的KL散度。由于这部分比较常规，且不具备太多改进的可能性，笔者这里就简单写一下。具体的内容需要仔细对应原文部分内容。

到此我们已经讲解完了模型的结构和模型的损失函数。

那么在生成图像的时候需要遵循以下流程：

随机Prior中的Zt并进行估计，然后更新画布矩阵ct。当循环T次画布矩阵更新完成，那么生成的图像是D(X|_ct)。需要注意的是，在生成图像的过程中，编码器是在全过程中都没有参与的。在下一个节中，我们将重点介绍read和write操作以及他们和visual attention的关系。

5. Read and Write 操作和注意力机制

文章中作者讲到，前述的DRAW模型结构，没有read和write，是不完整的。那么在这一节中，我们将重点分析read和write操作以及他们的特点。同时这里，笔者推荐几个开源的repository，都是可以实现的且做的非常好的实现：

1. Eric Jang的代码： https://github.com/ericjang/draw 这个仅复现了MNIST，笔者这里的内容以这个代码为例

2.Ilya Kostrikov NYU：https://github.com/ikostrikov/TensorFlow-VAE-GAN-DRAW

3. Natsu6767： https://github.com/Natsu6767/Generating-Devanagari-Using-DRAW

Read and write 不加入注意力

最简单实现DRAW的方式就是不加入注意力机制，每次都把整个图像作为编码器的输入，同时对整个解码器输出的画布矩阵进行修改。那么这样的话读和写的操作就可以退化为：

然而这种方法不允许编码器在创造latent distribution的时候，专注于输入的某个地方。 也同理，它本身不允许decoder每次只修改最终画布矩阵的一部分。因此，这可以认为是DRAW without Attention。那么与之相对的是selective attention的DRAW with Attention。

我们的选择性注意力模型是通过一个2D高斯滤波来实现的，通过将滤波器使用到图像上，可以产生一个图像“补丁”的平滑变化的位置和缩放。和所展示的一样，NxN的高斯滤波器被放置在图像的具体坐标处，并且使用步长距离来控制滤波器的采样间隔点和缩放距离。这意味着，大的步长会导致图像中更多部分被观测到，但是图像中的有效分辨率则会降低。网格中心坐标(gx, gy)和步长决定了滤波器的平均位置。

 

还有两个额外的参数在注意力网络中被需要使用。一个是高斯滤波器带有各向异性的方差参数，一个是标量的强度值gamma用来和滤波器的响应函数相乘。输入图像如果是一个AxB的图像，那么所有五个注意力参数都会被在每个时间步骤处动态决定。这个决定的方式是一种对于解码器输出的线性变换。

需要注意到是，代码中原来也有一个filterbank，就是用来产生注意力坐标的Fx和Fy。可被定义为：

这里，i和j参数都是注意力块的一个点，Zx和Zy是规范化常数用来控制总和为1。那么最后从图像层面的角度理解这一过程即：

那么了解了这个部分后，具体该怎么读和写？

• 读的操作：

输入—— Fx，Fy，强度gamma，和一个输入图像及对应的error image。

输出—— 一个拼接图[x, error image]

我在这里截取了一段代码来实现上述read的功能并对做出的解释进行验证。

def filterbank(gx, gy, sigma2,delta, N):
    grid_i = tf.reshape(tf.cast(tf.range(N), tf.float32), [1, -1])
    mu_x = gx + (grid_i - N / 2 - 0.5) * delta # eq 19
    mu_y = gy + (grid_i - N / 2 - 0.5) * delta # eq 20
    a = tf.reshape(tf.cast(tf.range(A), tf.float32), [1, 1, -1])
    b = tf.reshape(tf.cast(tf.range(B), tf.float32), [1, 1, -1])
    mu_x = tf.reshape(mu_x, [-1, N, 1])
    mu_y = tf.reshape(mu_y, [-1, N, 1])
    sigma2 = tf.reshape(sigma2, [-1, 1, 1])
    Fx = tf.exp(-tf.square(a - mu_x) / (2*sigma2))
    Fy = tf.exp(-tf.square(b - mu_y) / (2*sigma2)) # batch x N x B
    # normalize, sum over A and B dims
    Fx=Fx/tf.maximum(tf.reduce_sum(Fx,2,keep_dims=True),eps)
    Fy=Fy/tf.maximum(tf.reduce_sum(Fy,2,keep_dims=True),eps)
    return Fx,Fy

def attn_window(scope,h_dec,N):
    with tf.variable_scope(scope,reuse=DO_SHARE):
        params=linear(h_dec,5)
    # gx_,gy_,log_sigma2,log_delta,log_gamma=tf.split(1,5,params)
    gx_,gy_,log_sigma2,log_delta,log_gamma=tf.split(params,5,1)
    gx=(A+1)/2*(gx_+1)
    gy=(B+1)/2*(gy_+1)
    sigma2=tf.exp(log_sigma2)
    delta=(max(A,B)-1)/(N-1)*tf.exp(log_delta) # batch x N
    return filterbank(gx,gy,sigma2,delta,N)+(tf.exp(log_gamma),)

## READ ## 
def read_no_attn(x,x_hat,h_dec_prev):
    return tf.concat([x,x_hat], 1)

def read_attn(x,x_hat,h_dec_prev):
    Fx,Fy,gamma=attn_window("read",h_dec_prev,read_n)
    def filter_img(img,Fx,Fy,gamma,N):
        Fxt=tf.transpose(Fx,perm=[0,2,1])
        img=tf.reshape(img,[-1,B,A])
        glimpse=tf.matmul(Fy,tf.matmul(img,Fxt))
        glimpse=tf.reshape(glimpse,[-1,N*N])
        return glimpse*tf.reshape(gamma,[-1,1])
    x=filter_img(x,Fx,Fy,gamma,read_n) # batch x (read_n*read_n)
    x_hat=filter_img(x_hat,Fx,Fy,gamma,read_n)
    return tf.concat([x,x_hat], 1) # concat along feature axis

read = read_attn if FLAGS.read_attn else read_no_attn

通过代码不难看出，具有注意力的读取确实是先从attention window函数中提取出Fx，Fy和gamma。然后将x和代表error image的x_hat作为滤波器的输入对其进行滤波，后将二者拼接起来进行返回。这和我们前文所讲一致。

• 写的操作

从解码器输出的一组参数gamma‘，Fx’和Fy'被获取到，同时注意逆向换位问题。那么像素强度最终可以被反转为：

 

这里，wt是NxN的图像块，从ht时刻的解码器中获取。对于彩色图像来说，每个输入和输出，同时还有read和write的patch都是一个三通道的结果。

## WRITER ## 
def write_no_attn(h_dec):
    with tf.variable_scope("write",reuse=DO_SHARE):
        return linear(h_dec,img_size)

def write_attn(h_dec):
    with tf.variable_scope("writeW",reuse=DO_SHARE):
        w=linear(h_dec,write_size) # batch x (write_n*write_n)
    N=write_n
    w=tf.reshape(w,[batch_size,N,N])
    Fx,Fy,gamma=attn_window("write",h_dec,write_n)
    Fyt=tf.transpose(Fy,perm=[0,2,1])
    wr=tf.matmul(Fyt,tf.matmul(w,Fx))
    wr=tf.reshape(wr,[batch_size,B*A])
    #gamma=tf.tile(gamma,[1,B*A])
    return wr*tf.reshape(1.0/gamma,[-1,1])

write=write_attn if FLAGS.write_attn else write_no_attn

这里的复现是write操作，可以看出，首先将其输入一个全连接，然后reshape权重参数后利用同一个attention window对三个参数进行提取，然后进行转置并对其进行操作，可以看出具体的操作公式与公式（29）一致。

 

结束语

到此，笔者粗浅地介绍了著名的研究工作 DRAW: A Recurrent Neural Network for Image Generation。整体来说这个算法的设计十分的自然，同时符合人类视觉规律。但是仍旧存在一些问题，如损失函数的设计，LSTM的编码特征不高效充分，模型不收敛，参数敏感，大尺寸图像恢复效果较差等等。笔者将在毕业设计的研究工作中将逐一对这类问题进行分析和讨论。同时，该文章中提到的思想可以广泛应用于不同研究领域，如：图像质量评价，图像恢复，图像去噪等。这样一个研究工作是具备十分充分的可扩展性的，同时也具有很大的研究价值。希望可以通过这篇文章对该工作的解析，让更多人能够发现这一工作的闪光点和潜在价值。如有疑问请在评论区留言讨论，谢谢！