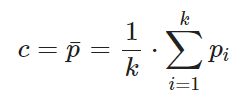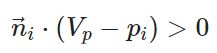点云表面法线估计
平面的法线是垂直于它的单位向量。点云的表面法线则被定义为垂直于与点云表面相切的平面的单位向量。表面法线也可以计算点云中一点的法线,这是一种十分重要的性质。给定一个几何表面,通常很难将表面某个点的法线方向推断为垂直于该点表面的向量。但是,由于我们获取的点云数据集是真实表面上的一组点样本,因此有两种可能性:
- 使用表面网格化技术从获取的点云数据集中获取基础表面,然后从网格中计算表面法线;
- 使用近似值直接从点云数据集中推断表面法线。
PCL中使用后者,即给定点云数据集,直接计算点云中每个点的表面法线。
理论基础
尽管有许多不同的法线估计方法,但其中最简单也最常见的一个是最小二乘法,确定表面一点法线的问题近似于估计表面的一个相切面法线的问题,因此转换过来以后就变成一个最小二乘法平面拟合估计问题。
法线计算
我们通常将平面表示为一个点c和一个法向量![]() ,则从一个点
,则从一个点![]() 到平面的距离可以定义为
到平面的距离可以定义为![]() ,中心点c和
,中心点c和![]() 则是通过最小二乘法以使
则是通过最小二乘法以使 ![]() 得到的:
得到的:
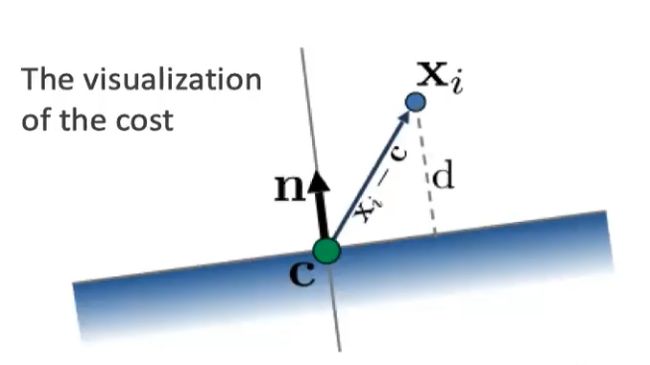
假如有一堆点 ![]() ,查找一个超平面,使通过点c的一个法向量
,查找一个超平面,使通过点c的一个法向量![]() 满足周围点的向量
满足周围点的向量![]() 在法向量
在法向量![]() 上的投影之和最小(两个向量的乘积即是一个向量在另一个向量上的投影):
上的投影之和最小(两个向量的乘积即是一个向量在另一个向量上的投影):
c作为![]() 的中心,法向量
的中心,法向量![]() 的值是通过分析点集合
的值是通过分析点集合![]() 的协方差矩阵
的协方差矩阵![]() 的特征值和特征向量得到的(PCA—主成分分析),对于指定区域的点集合
的特征值和特征向量得到的(PCA—主成分分析),对于指定区域的点集合![]() ,其协方差矩阵定义如下:
,其协方差矩阵定义如下:
C是一个对称的半正定矩阵,k是点数目,![]() 是周围点的质心,
是周围点的质心,![]() 是协方差矩阵的第j个特征值
是协方差矩阵的第j个特征值![]() →是协方差矩阵的第j个特征向量。通过以下代码可以计算质心和协方差矩阵:
→是协方差矩阵的第j个特征向量。通过以下代码可以计算质心和协方差矩阵:
// 定义一小块表面区域的协方差矩阵
Eigen::Matrix3f covariance_matrix;
// 定义一小块表面区域的质心坐标
Eigen::Vector4f xyz_centroid;
// 计算质心坐标
pcl::compute3DCentroid(*cloud, xyz_centroid);
// 计算3x3的协方差矩阵
pcl::computeCovarianceMatrix(*cloud , xyz_centroid, covariance_matrix);表面曲率通过协方差矩阵的特征值进行估算得到:
其中![]() 。
。
法线方向问题
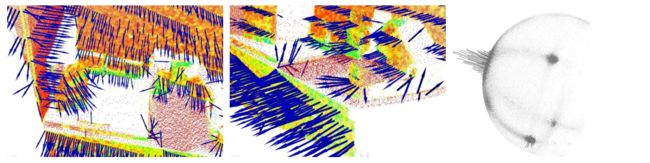
没有直接的数学方法可以解决法线的朝向问题,例如下边的左图和中图,该数据及来自厨房环境的一部分。很明显图中的法线并非朝着一个方向。右图为所有法线合并成的扩展高斯图(EGI),也称为法线球体(Normal Sphere),它描述了点云中所有法线的方向。由于数据是2.5维的(即数据只从单一视角获取),其法线也应该仅是一个半球体的扩展高斯图,但由于我们没有定下法线的方向,所以这些法线遍布球体。
但是,如果我们有了视点Vp,此问题就迎刃而解了。我们让所有法线n→选取其朝向视点的那个方向即可:
上图即为将所有法线重新定向之后的效果和其对应的扩展高斯图EGI。
比例因子的选择
如前所述,需要根据该点的周围点邻域,也称为k-neighborhood(k邻域)来估算该点的表面法线。 最近邻估计则面临选择正确的比例因子的问题:给定采样点云数据集,如何选择正确的k(通过pcl::Feature::setKSearch给出)或r(通过pcl::Feature::setRadiusSearch 给出)值来确定点的最近邻?
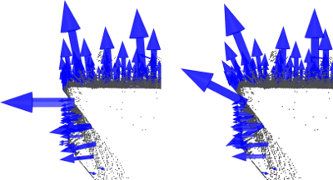
这个问题非常重要,是点特征表示的自动估计(即在没有用户给定阈值的情况下)的限制因素。为了更好地说明此问题,下图显示了选择较小的比例(即较小的r或k)与较大的比例(即较大的r或k)的效果。左图选择的比例因子较为合理,其估计的表面法线大致垂直于两个平面,并且其小边缘被较好的保留。但是,如果选择的比例因子太大(右图),则相邻对象的集合会覆盖相邻表面的较大点,因此估计的点要素表示会失真,在两个平面边缘处,旋转的曲面法线会被涂抹,边缘和细节被忽略。
因此,必须根据实际应用所需的精度来选择确定点的邻域的比例。简而言之,如果杯子的手柄和圆柱部分之间的边缘处的曲率很重要,则比例因子必须足够小以捕获这些细节,否则要大。
注:
默认视点坐标为(0,0,0),可通过以下代码修改:
setViewPoint(float vpx, float vpy, float vpx);计算表面法向量内部伪代码:
// 遍历每个点云P中的点p
for each point p in cloud P
// 得到p点的最近邻
1. get the nearest neighbors of p
// 计算p点的表面法线n
2. compute the surface normal n of p
// 检查n的方向是否指向视点,如果不是则进行反转
3. check if n is consistently oriented towards the viewpoint and flip otherwise代码实现
#include
#include
#include
#include
#include
/**
* 法向量估计
*/
int main() {
// 加载点云
pcl::PointCloud::Ptr cloud(new pcl::PointCloud);
pcl::io::loadPCDFile("G:/vsdata/PCLlearn/PCDdata/bun0.pcd", *cloud);
// 法线对象
pcl::PointCloud::Ptr normals(new pcl::PointCloud);
// 用于法线估计的对象
pcl::NormalEstimation normalEstimation;
normalEstimation.setInputCloud(cloud);
// 对于每个点,使用半径为3cm的所有邻域
normalEstimation.setRadiusSearch(0.03);
// 通过kd树使搜索更加高效
// 法线估计对象将使用它来查找最近的邻点
pcl::search::KdTree::Ptr kdtree(new pcl::search::KdTree);
normalEstimation.setSearchMethod(kdtree);
// 计算法线
normalEstimation.compute(*normals);
// 法线可视化
pcl::visualization::PCLVisualizer viewer("PCL Viewer");
viewer.setBackgroundColor(0.0, 0.0, 0.5);
viewer.addPointCloud(cloud, "cloud");
// 参数int level=2 表示每2个点绘制一个法向量
// 参数float scale=0.01 表示法向量长度缩放为0.01倍
viewer.addPointCloudNormals(cloud, normals, 2, 0.01, "normals");
// viewer.addCoordinateSystem(0.1); //添加坐标系
while (!viewer.wasStopped()) {
viewer.spinOnce();
}
return 0;
} 效果:
积分图估算点云法线
积分图像是对有序点云进行法线估计的一种方法。该算法把点云作为一个深度图像,并创建一定的矩形区域来计算法线,考虑相邻像素关系,而无需建立树形查询结构。因此,它是非常有效的。但此方法进行法线估计只适用于有序点云,对于无序点云就只能采用其他方法。
#include
#include
#include
#include
int main()
{
// 加载点云
pcl::PointCloud::Ptr cloud(new pcl::PointCloud);
pcl::io::loadPCDFile("G:/vsdata/PCLlearn/PCDdata/table_scene_mug_stereo_textured.pcd", *cloud);
// 法线对象
pcl::PointCloud::Ptr normals(new pcl::PointCloud);
// 创建一个用于法线估计的对象并计算法线
pcl::IntegralImageNormalEstimation ne;
// 有以下可选的估算方式:
/**
enum NormalEstimationMethod
{
COVARIANCE_MATRIX,
AVERAGE_3D_GRADIENT,
AVERAGE_DEPTH_CHANGE
};
COVARIANCE_MATRIX模式创建9个积分图像,以根据其局部邻域的协方差矩阵为特定点计算法线。
AVERAGE_3D_GRADIENT模式创建6个积分图像以计算水平和垂直3D渐变的平滑版本,并使用这两个渐变之间的叉积计算法线。
AVERAGE_DEPTH_CHANGE模式仅创建单个积分图像,并根据平均深度变化计算法线。
*/
ne.setNormalEstimationMethod(ne.AVERAGE_3D_GRADIENT);
ne.setMaxDepthChangeFactor(0.02f);//设置深度变化的阀值
ne.setNormalSmoothingSize(10.0f);//设置计算法线的区域
ne.setInputCloud(cloud);
ne.compute(*normals);//计算
// 法线可视化
pcl::visualization::PCLVisualizer viewer("PCL Viewer");
viewer.setBackgroundColor(0.0, 0.0, 0.5);
viewer.addPointCloudNormals(cloud, normals);
while (!viewer.wasStopped()) {
viewer.spinOnce();
}
return 0;
} 效果: