【刷题】刷题总结

刷题总结

---

---

前言

这是一个错题本，将刷题中犯的一些错误总结下来。文章会不断更新，欢迎收藏转发。

---

一、刷题原则（每天刷多少、按照什么顺序、要不要看答案、刷题建议）

LeetCode、NowCode刷题，要按什么顺序刷，每道题刷几遍，每道题目刷到什么程度。我阅读了大量资料，同时一边刷题一边总结经验，将自己的整理经验记录下来，供自己日后查阅，也分享给大家。

1.每天刷多少
每天刷多少道题视自己的时间而定，不同难度的题目对时间消耗有很大区别，但至少每天一道，让自己保持手感，并且持续积累。切记，重在坚持。
2.按照什么顺序
不要按照默认的顺序。
可以按照题目类型去刷，在没有掌握题目类型的情况下，一个类型刷三五道直到掌握，掌握相应方法后，就间歇性的刷这个类型1的题目。
3.要不要看答案，自己做多久做不出来就看答案，做出来了要不要看答案
第一遍做题的目的是为了见大量题型，积累做题思路，所以十几二十分钟没有思路就可以看答案，看答案可以浏览几个效率高，点赞多的答案，掌握稳定解法，积累优秀解法。做出来的题目也建议看答案，花几分钟浏览一下常用的思路，遇到好的思路、知识盲区就积累下来。
4.参考链接

• 美团金融｜安卓客户端｜面经【 3 轮技术面 + 1 轮 HR 面】（21 届秋招）｜2021｜
• 2021秋招算法总结1-DFS篇
• 关于leetcode刷题详细介绍
• 【LeetCode攻略】使用LeetCode刷题时你必须注意的几个点
• Leetcode刷题指南和top100题目
• LeetCode 按照怎样的顺序来刷题比较好？
• 求助｜请问刷多少题才能达到找工作的基础线？

5.刷题建议
首先上结论：刷完200常见题，每道题都能保证 20min内bug-free写出暴力解 + 20min内bug-free写出（次优解 / 最优解)就非常稳了

我觉得题数完全没用处
对算法的理解&熟练度 / 周赛成绩更能说明面试表现

我就刷了160题 (https://leetcode.com/yiyangiliu/ )
但是我周赛最好成绩是1.2k/11k（对应中国站450名左右）
别的周赛平均做出2道，名次[1.5k-3.5k]/10k吧

找实习时面了很多家，有三家出的题没见过（腾讯 滴滴 字节），有一家出了hard题（滴滴）（btw这道hard写了20min），都写出来了，最后从了方向最喜欢的字节。
我觉得攀比刷题数真的是个误区，从来不是刷题多=nb，而是面试能做出来=nb。

如果训练的话，应该这样练习：限时20min，不能写出bug-free代码就算不会。明天继续尝试
（以上也是我的刷题方法）
因为此时如果在面试，你和面试官已经大眼瞪小眼20分钟了，要多尴尬有多尴尬

再说一下时间分配吧，我一般刷题半下午+半晚上吧，有时候上午也刷刷。

以上说的当然不是为了卷或鸡汤，因为我在数量这一方面其实挺“失败”的，我这样刷了两个月才刷到160题，其中还包括6次周赛一天4题的“跃进”，如果去掉打周赛做的题，为了面试刷的题可能低于130道。

结果就是俩月130题，平均每天2题稍多点，这速度已经弟弟得不行了。

但是其实无所谓，因为我的刷题方法比较“solid”，并且我周赛成绩不错，所以我在找工之前就比较有安全感。我觉得面试题不会比周赛第二/三题更难，结果也确实如此。

二、还没看答案题目

2.1 不会做没看答案

• 树上游戏
• 最小值
• 穿越银河

2.2 做了没看答案

• 131. 分割回文串
• 1002. 查找常用字符（哈西表）
• 1380. 矩阵中的幸运数
• 169. 多数元素
• 240. 搜索二维矩阵 II
• 面试题 02.03. 删除中间节点——>解答（搞定常见链表问题）
• 212. 单词搜索 II
• 剑指 Offer 12. 矩阵中的路径

三、牛客

1. JZoffer错误

• JZ14 链表中倒数第k个结点
  正确思路
  网络思路：双指针，一根指针先走k步（边走边判断是否为空，因为链表长可能小于k），最后两根指针一起走，前面那根指针为空时后面的指针所指即为所求 。
  我的思路：第一次循环获取链表长度 Len，将倒数第k个转化为整数第 Len-k+1 个，顺向去找，直到达到位置。
  提交错误
  assert(pHead);
  这行代码导致如下错误，去掉这行代码即可
  运行错误:请检查是否存在数组、列表等越界非法访问，内存非法访问等情况
  a.out: ./solution.h:22: ListNode *Solution::FindKthToTail(ListNode *, int): Assertion `pHead’ failed.

• JZ15 反转链表
  总结
  指针就是指向数据的一个标志，本身并没有数据的内存空间，但通过指针可以操作数据，改变数据结构关联关系。使用指针时要注意指针赋值的先后关系，避免对一个指针操作时造成后续无法操作的情况。

例如删除链表头结点时，先让指针指向下一位置，避免指针找不到链表
SLinkList* p; //p指向了一个链表
SLinkList* cur = p;
p = p->_pNext;
free(cur);
cur = NULL;
return p;

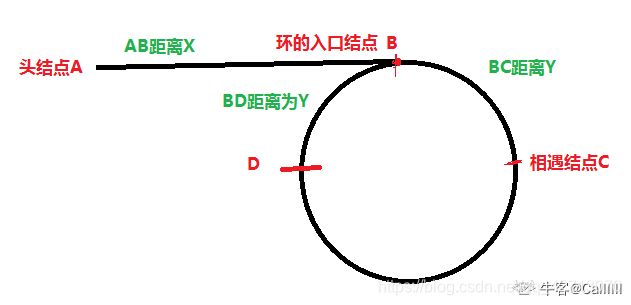
• JZ55 链表中环的入口结点

**** 第一次编写时的错误记录
    SListNode* EntryNodeOfLoop(SListNode* pHead) {
        SListNode* cur1 = pHead;
        vector<SListNode*> saveV;
        while(cur1){
            for(int isV=0;isV<saveV.size();isV++){
                if(saveV[isV]==cur1){return cur1;}
                ///错误的保存方式，根本无法进入循环
                if(isV==saveV.size()-1)
                	{saveV.push_back(cur1);}
            }
            cur1 = cur1->_pNext;
        }
        return NULL;
    }

**** 修改后
    SListNode* EntryNodeOfLoop(SListNode* pHead) {
        SListNode* cur1 = pHead;
        vector<SListNode*> saveV;
        while(cur1){
            for(int isV=0;isV<saveV.size();isV++){
                if(saveV[isV]==cur1){return cur1;}
            }
            ///将添加移动到这里
            saveV.push_back(cur1);
            cur1 = cur1->_pNext;
        }
        return NULL;
    }
    
**** 网络解答 一
    ListNode* EntryNodeOfLoop(ListNode* pHead)
    {
        unordered_set<ListNode*> st;
        while (pHead) {
            if (st.find(pHead) == st.end()) {
                st.insert(pHead);
                pHead = pHead->next;
            }
            else {
                return pHead;
            }
        }
        return nullptr;
    }
};

**** 网络解答 二（偏数学）
初始化：快指针fast指向头结点， 慢指针slow指向头结点
让fast一次走两步， slow一次走一步，第一次相遇在C处，停止
然后让fast指向头结点，slow原地不动，让后fast，slow每次走一步，当再次相遇，就是入口结点。
理解方法，在C点快慢指针相差一圈，且快指针走了两圈，慢指针走了一圈；而慢指针又是从头结点出发，此时慢指针距节点入口距离就是头结点至节点入口距离。

• 容器里保存的是变量的值而不是变量，变量变化（甚至变量不复存在）时，容器中对应的值不发生变化

//例一
int a;
vector<int> save;
a=1;
save.push_back(a);
a=2;
save.push_back(a);
//此时，save里面保存的是[1, 2];

//例二
vector<int> save;
for（int i=0;i<5;i++）
{
	int a;
	a=i;
	save.push_back(a);
}
//循环结束后，a不复存在，但容器中的值仍然存在，为[1, 2, 3, 4, 5]
	

• JZ48_不用加减乘除做加法

不会做

参考官方思路
	无进位和运算就是按位异或结果，进位就是与运算结果但是需要左移一位，因为进位影响下一位的运算。
所以s = a + b,其实就是无进位和+进位的结果。
算法步骤：
	计算a和b的无进位和，和进位
	如果进位不为0，则说明a+b的结果等于无进位和+进位，此时，把无进位和作为a，进位作为b，继续计算
	如果进位等于0， 说明此时a+b的结果就等于无进位和，返回无进位和即可。

题解
    int Add(int num1, int num2) {

        int he = num1^num2;
        int jw = (num1&num2)<<1;

        if(jw==0)
            return he;
        return Add(he, jw);
    }

• JZ47 求1+2+3+…+n
  题目：求1+2+3+…+n，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

//网络思路：使用·短路与实现if，使用递归实现while

//网络题解一：
    int Sum_Solution(int n) {
        int ans = n;
        ans && (ans += Sum_Solution(n - 1));
        return ans;
    }
//网络题解二：
    int Sum_Solution(int n) {
        return (pow(n,2)+n)>>1;
    }

• JZ60 把二叉树打印成多行
  出现如下错误：（段错误:您的程序发生段错误，可能是数组越界，堆栈溢出（比如，递归调用层数太多）等情况引起。）
  可能原因：
  1.递归无法结束，循环无法结束；
  2.遇到输入数据量为零的情况没有直接返回。

• 剑指 Offer 54. 二叉搜索树的第k大节点

//题目本身不难，但做题过程中出现一个错误，积累下这个知识点：
//函数的形参指针，作为指针变量可以将其所指地址保存的内容传出来。
//但是！如果在函数内部直接修改指针内容，即指针所指向的地址是无法传出的。

//例一（正确）：（如果root->val=4,则输出4）
    int kthLargest(TreeNode* root, int k) {
        int a=3;
        int* myout=&a;
        Reverse_traversal(root, myout);
        cout<<*myout<<endl;
	}
	int Reverse_traversal(TreeNode* root, int* myout)
    {
    	*myout = root->val;//将指针对应地址内容赋值
    	return 1;
    }

//例二（错误）：（如果root->val=4,仍然输出3）
    int kthLargest(TreeNode* root, int k) {
        int a=3;
        int* myout=&a;
        Reverse_traversal(root, myout);
        cout<<*myout<<endl;
	}
	int Reverse_traversal(TreeNode* root, int* myout)
    {
    	myout = &root->val;//改变指针指向的地址，但出了函数不起作用
    	return 1;
    }

2. 研发常考题目

• NC4 判断链表中是否有环

我的答案

//快慢指针

参考网络思路

//哈希表保存访问过的结点
    bool hasCycle(ListNode *head) {
        ListNode* cur=head;
        unordered_map<ListNode*, int> save;
        while(cur)
        {
            if(save.find(cur)!=save.end())
                return 1;
            save[cur] = 1;
            cur = cur->next;
        }
        return 0;
    }

网络答案思路

//set,不可插入新内容则有重复，链表为环
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head==NULL)
            return false;
        set<ListNode *> s;
        ListNode *p = head;
        while(p!=NULL)
        {
！！！！！！ 注意这句话
            if(!s.insert(p).second)//不可插入新内容则有重复，链表为环
 
            {
                 return true;
            }
            else
                p=p->next; //指向下个节点
        }
        return false;
    }
};

• NC22 合并两个有序的数组
  我的答案

    void merge(int A[], int m, int B[], int n) {
        int posM=m-1, posN=n-1;
        for(int i=m+n-1; i>=0;i--)
        {
            if(posN==-1)
            {
                A[i]=A[posM];
                posM--;
                continue;
            }
            if(posM==-1)
            {
                A[i]=B[posN];
                posN--;
                continue;
            }
            
            if(A[posM]>B[posN])
            {
                A[i]=A[posM];
                posM--;
            }else if(A[posM]<=B[posN]){
                A[i]=B[posN];
                posN--;
            }
        }
    }

网络答案（代码优化）

/*
     * 最优解：从后往前处理,不需要开辟额外空间
     * Runtime: 0 ms.Your runtime beats 45.38 % of java submissions.
     */
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i = m - 1, j = n - 1, index = m + n - 1;
        while (i >= 0 && j >= 0)
            nums1[index--] = nums1[i] > nums2[j] ? nums1[i--] : nums2[j--];
        while (j >= 0)
            nums1[index--] = nums2[j--];
    }

四、LeetCode

1.解答学习

• 剑指 Offer 32 - II. 从上到下打印二叉树 II

//我的方法：定义1两个队列，一个保存孩子结点，一个保存层数
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int> > out;
        levelPrint(root, out);
        return out;
    }

    int levelPrint(TreeNode* root, vector<vector<int> >& out)
    {
        if(root==NULL)
            return 0;
        queue<TreeNode*> TreeNodeSave;
        queue<int> TreeLeyer;

        vector<int> CurLayerVal;

        TreeNodeSave.push(root);
        TreeLeyer.push(1);
        int lastLayer = 1;
        while(TreeNodeSave.size())
        {
            if(TreeLeyer.front()==lastLayer+1)
            {
                out.push_back(CurLayerVal);
                CurLayerVal.clear();
            }
            CurLayerVal.push_back(TreeNodeSave.front()->val);
            if(TreeNodeSave.front()->left)
            {
                TreeNodeSave.push(TreeNodeSave.front()->left);
                TreeLeyer.push(TreeLeyer.front()+1);
            }    
            if(TreeNodeSave.front()->right)
            {
                TreeNodeSave.push(TreeNodeSave.front()->right);
                TreeLeyer.push(TreeLeyer.front()+1);    
            }
            lastLayer=TreeLeyer.front();
            TreeNodeSave.pop();
            TreeLeyer.pop();
        }
        out.push_back(CurLayerVal);
        return 1;
    }
};

//网络题解：只定义一个队列，通过一个小循环，
//使得每次大循环访问到所有同层孩子结点，
//通过最开始保存一个size变量实现同层孩子数量记录的
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ans;
        if(root == nullptr)     return ans;
        queue<TreeNode*> myQue;
        myQue.push(root);
        while(!myQue.empty()){
            vector<int> tmp;
            int size = myQue.size();
            for(;size--;myQue.pop()){
                auto node = myQue.front();
                if(node->left)      myQue.push(node->left);
                if(node->right)     myQue.push(node->right);               
                tmp.push_back(node->val);
            }
            ans.push_back(tmp);
        }
        return ans;
    }
};

• _1022. 从根到叶的二进制数之和

//我的思路：递归循环到每个叶子结点，把存的所有二进制数转为十进制，提取所有十进制数，求和；

//网络思路：
class Solution {
public:
    int sumRootToLeaf(TreeNode* root) {
        return findNum( root, 0);
    }

    int findNum(TreeNode* root, int sum)
    {
        if(root==NULL)
            return 0;
        sum = sum*2+root->val;
        if(root->left==NULL&&root->right==NULL)
            return sum;
        return (findNum(root->left, sum)+findNum(root->right, sum));
    }
};

• _897. 递增顺序查找树

//我的思路：
//首先保证首节点没有左子树；
//然后，访问cur和curNext，if(curNect->left) 重组链接关系；

//网络解析：
class Solution {
    /**
     * 递增顺序查找树
     *
     * @param root
     * @return
     */
    TreeNode head = new TreeNode(0);
    TreeNode real = head;
    public TreeNode increasingBST(TreeNode root) {
        if (root == null) {
            return null;
        }

        increasingBST(root.left);
        real.right = new TreeNode(root.val);
        real = real.right;
        increasingBST(root.right);
        return head.right;
    }
}

• 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
  题目描述：给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

我的思路：访问节点，查询其左子树是否包含pq，右子树是否包含pq直到左或右不同时包含pq，当前节点为目标。由于调用查找结点函数，时间复杂度很高。

网络思路：二叉搜索树性质，左子树的数小于节点，右子树的数大于节点，循环判断。

• _617. 合并二叉树

我的解法（复杂）：
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(!root1)
            return root2;
        if(!root2)
            return root1;
        if(root1&&root2)
            root1->val += root2->val;
        Hebing( root1,  root2);
        return root1;
    }

    void Hebing(TreeNode* root1, TreeNode* root2)
    {
        if(root1->left && root2->left)
        {
            root1->left->val = root1->left->val + root2->left->val;
            Hebing(root1->left, root2->left);
        }else if(!root1->left && root2->left)
        {
            root1->left = root2->left;
        }

        if(root1->right && root2->right)
        {
            root1->right->val = root1->right->val + root2->right->val;
            Hebing(root1->right, root2->right);
        }else if(!root1->right && root2->right)
        {
            root1->right = root2->right;
        }
    }
};

网络解法（简单）：
class Solution {
    public TreeNode mergeTrees_1(TreeNode t1, TreeNode t2) {
        if (t1 == null) {
            return t2;
        }
        if (t2 == null) {
            return t1;
        }
        // 先合并根节点
        t1.val += t2.val;
        // 再递归合并左右子树
        t1.left = mergeTrees(t1.left, t2.left);
        t1.right = mergeTrees(t1.right, t2.right);
        return t1;
    }
     /**
     * 不修改原二叉树的解法
     */
    public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
        if (t1 == null && t2 == null) {
            return null;
        }
        // 先合并根节点
        TreeNode root = new TreeNode((t1 == null ? 0 : t1.val) + (t2 == null ? 0 : t2.val));
        // 再递归合并左右子树
        root.left = mergeTrees(t1 == null ? null : t1.left, t2 == null ? null : t2.left);
        root.right = mergeTrees(t1 == null ? null : t1.right, t2 == null ? null : t2.right);
        return root;
    }
}

• 面试题 04.06. 后继者
  题目描述：设计一个算法，找出二叉搜索树中指定节点的“下一个”节点（也即中序后继）。如果指定节点没有对应的“下一个”节点，则返回null。

网络解答一：先来个直观一点的， 找到p， 然后取p的后一个节点。
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        TreeNode * res = nullptr, * prev = nullptr;
        inorderTraversal(root, prev, p, res);
        return res;
    }
    void inorderTraversal(TreeNode * root, TreeNode*& prev, TreeNode *p, TreeNode*& res ){
        if(root == nullptr || res != nullptr) return;
        inorderTraversal(root->left, prev, p, res);
        if(prev == p) res = root;
        prev = root;
        inorderTraversal(root->right, prev, p, res);
    }
};
网络解答二：再来个简洁一点的，我们要找的是第一个大于p->val的节点， 所以遇到第一个大于p->val的即可返回。
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        if(root == nullptr) return nullptr;
        TreeNode * res = inorderSuccessor(root->left, p);
        if(res != nullptr) return res;
        if(root->val > p->val) return root;
        return inorderSuccessor(root->right, p);
    }
};

我的答案：
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
        int Flag = 0;
        int* pFlag = &Flag;
        if(!root)
            return NULL;
        TreeNode* out = NULL;
        out = Inorder(root, p, pFlag);
        return out;
    }
    TreeNode* Inorder(TreeNode* root, TreeNode* p, int* pFlag)
    {
        if(root->left)
        {
            TreeNode* out = Inorder(root->left, p, pFlag);
            if(out!=NULL)
                return out;
        }
        if(*pFlag==1)
        {
            cout<<"**2:"<<root->val<<endl;
            return root;
        }
        if(root==p)
        {
            *pFlag = 1;
            cout<<"**"<<root->val<<endl;
        }
        if(root->right)
        {
            TreeNode* out = Inorder(root->right, p, pFlag);
            if(out!=NULL)
                return out;
        }
        cout<<"**x:"<<root->val<<endl;
        return NULL;
    }
};

• _993. 二叉树的堂兄弟节点

网络解答：深度优先
class Solution {
    int deep1, deep2;
    TreeNode *pra1,  *pra2;
    void node_deep(TreeNode* root, TreeNode* pra,int deep, int x, int y)
    {
        if(!root) return;
        if(root->val == x)
        {
            pra1 = pra;
            deep1 = deep+1;
        }
        if(root->val == y)
        {
            pra2 = pra;
            deep2 = deep+1;
        }
        node_deep(root->left,root,deep+1,x,y);
        node_deep(root->right,root,deep+1,x,y);
    }
public:
    bool isCousins(TreeNode* root, int x, int y) {
        if(!root) return false;
        node_deep(root,NULL,0,x,y);
        return (deep1 == deep2) && (pra1 != pra2);
    }
};

• _1305. 两棵二叉搜索树中的所有元素
  注意函数
  merge(v1.begin(),v1.end(), v2.begin(), v2.end(), back_inserter(ret))

网络答案：
class Solution {
public:
    vector<int> getAllElements(TreeNode* root1, TreeNode* root2) {   
        vector<int> v1, v2, ret;
        mid(root1, v1);
        mid(root2, v2);
        merge(v1.begin(),v1.end(), v2.begin(), v2.end(), back_inserter(ret));//注意
        return ret;
    }
    void mid(TreeNode* root, vector<int> &v) {
        if(root) {
        if(root->left) mid(root->left, v);
        v.push_back(root->val);
        if(root->right) mid(root->right, v);
        }
    }
};

• _53. 最大子序和
  题目描述：给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

以下是网络解答

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int res = nums[0];
        int sum = 0;
        for (int num : nums) {
            if (sum > 0)
                sum += num;
            else
                sum = num;
            res = max(res, sum);
        }
        return res;        
    }
};

以下是我的答案

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.size()==0)
            return -1;

        int maxSum=nums[0];
        for(int i=0;i<nums.size();i++)
        {
            if(nums[i]>maxSum)
                maxSum = nums[i];
        }
        if(maxSum>0)
        {
            maxSum = 0;
            int sum=0;
            for(int i=0;i<nums.size();i++)
            {
                sum += nums[i];
                if(sum<0)
                {
                    sum = 0;
                }
                if(sum>maxSum)
                {
                    maxSum = sum;   
                }
            }
        }
        return maxSum;
    }
};

• _70. 爬楼梯
  这道题目可以用递归，动态规划，数学解析等方法实现。

//递归
//可以直接递归，也可以做有缓存的递归

//动态规划
//从1循环到n
//分别存储每次的解

• 面试题 16.17. 连续数列 看一下分治

//网络答案
    //分治Time:O(NlogN) Space:O(logN)
    public int maxSubArray(int[] nums) {
        return divide(nums, 0, nums.length - 1);
    }
    private int divide(int[] nums, int st, int ed) {
        if(st == ed) return nums[st];
        int mid = (st + ed) / 2;
        //最大连续数列在mid的左边
        int left = divide(nums, st, mid);
        //最大连续数列在mid的右边
        int right = divide(nums, mid + 1, ed);
        //最大连续数列在中间包括mid
        //[i...mid...j]为最大练习数列
        int maxLeft = Integer.MIN_VALUE; // 记录[i...mid]最大和
        int sumLeft = 0;
        int maxRight = Integer.MIN_VALUE; // 记录[mid+1..j]最大和
        int sumRight = 0;
        for(int i = mid; i >= st; i--) {
            sumLeft += nums[i];
            maxLeft = Math.max(maxLeft, sumLeft);
        }
        for(int j = mid + 1; j <= ed; j++) {
            sumRight += nums[j];
            maxRight = Math.max(maxRight, sumRight);
        }
        //返回上面三种情况的最大值即可
        return Math.max(Math.max(left, right), maxLeft + maxRight);
    }

    //动态规划
    public int maxSubArray2(int[] nums) {
        int sum = 0;
        int max = Integer.MIN_VALUE;
        for(int num : nums) {
            max = Math.max(max, sum + num);
            if(sum + num < 0){
                sum = 0;
            }else {
                sum += num;
            }
        }
        return max;
    }
    //暴力Time:O(N^2) Space:O(N)
    public int maxSubArray1(int[] nums) {
        int max = Integer.MIN_VALUE;
        int[] preSum = new int[nums.length + 1];
        //前缀和
        for(int i = 1; i <= nums.length; i++) {
            preSum[i] = preSum[i-1] + nums[i-1];
        }
        for(int i = 0; i < nums.length; i++) {
            for(int j = 0; j <= i; j ++) {
                max = Math.max(max, preSum[i+1] - preSum[j]);
            }
        }
        return max;
    }

• _392. 判断子序列

//双指针
bool isSubsequence(char * s, char * t){
    while (*s && *t) {
        if (*s == *t) {
            s++;
        }
        t++;
    }
    if (*s == '\0') {
        return true;
    } else {
        return false;
    }
}

//思路一：库函数
class Solution:
    def isSubsequence(self, s: str, t: str) -> bool: 
        loc = -1
        for a in s:
            loc = t.find(a, loc + 1)
            if loc == -1:
                return False
        return True

//思路二：生成迭代器
class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        t = iter(t)
        return all(c in t for c in s)

//思路四：二分法
class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:  
        from collections import defaultdict
        import bisect
        lookup = defaultdict(list)
        for idx, val in enumerate(t):
            lookup[val].append(idx)
        # print(lookup)
        loc = -1
        for a in s:
            j = bisect.bisect_left(lookup[a], loc + 1)
            if j >= len(lookup[a]): return False
            loc = lookup[a][j]
        return True

//网络方法
    int largestSumAfterKNegations(vector<int>& A, int K) 
    {
        sort(A.begin(),A.end());
        int j = 0;
        int i = 0;
        
        for(; i < A.size()&& A[i] <0 && K>0;i++)
        {
            A[i] = -A[i];
            K--;
        }
        sort(A.begin(),A.end());
        while(K)
        {
            A[0] = -A[0];
            K--;
        }
        int sum = accumulate(A.begin(),A.end(),0);
        return sum;
    }

//我的方法
class Solution {
public:
    int largestSumAfterKNegations(vector<int>& A, int K) {
        sort(A.data() , A.data()+A.size());
        if(A[0]>=0)
        {    
            if(K%2==1)
                A[0]=-A[0];
        }else
        {
            for(int i=0;i<A.size()&&K;i++)
            {
                if(A[i]<0)    
                {
                    A[i]=-A[i];
                    K--;
                }else{
                    if(K%2==1)
                    {
                        if(A[i]<A[i-1])
                            A[i]=-A[i];
                        else
                            A[i-1]=-A[i-1];
                    }
                    K=0;
                }
            }
        }

        int sum=0;
        for(int i=0;i<A.size();i++)
            sum+=A[i];
        return sum;
    }
};

//我的答案（超时  ）
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<int> CurP(2,0);
        return Ways(CurP, -1, m, n);
    }

    int Ways(vector<int> CurP, int Move, int m, int n )
    {
        if(Move==0)
            CurP[0] ++;
        if(Move==1)
            CurP[1] ++;

        if(CurP[0]==m-1&&CurP[1]==n-1){
            return 1;
        }

        if(CurP[0]>m-1||CurP[1]>n-1){
            return 0;
        }
        return Ways(CurP , 0 , m, n)+Ways(CurP, 1, m, n);
    }

};

• _118. 杨辉三角

//网络答案
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> res={
        {1},
        {1,1},
        {1,2,1},
        {1,3,3,1},
        {1,4,6,4,1},
        {1,5,10,10,5,1},
        {1,6,15,20,15,6,1},
        {1,7,21,35,35,21,7,1},
        {1,8,28,56,70,56,28,8,1},
        {1,9,36,84,126,126,84,36,9,1},
        {1,10,45,120,210,252,210,120,45,10,1},
        {1,11,55,165,330,462,462,330,165,55,11,1},
        {1,12,66,220,495,792,924,792,495,220,66,12,1},
        {1,13,78,286,715,1287,1716,1716,1287,715,286,78,13,1},
        {1,14,91,364,1001,2002,3003,3432,3003,2002,1001,364,91,14,1},
        {1,15,105,455,1365,3003,5005,6435,6435,5005,3003,1365,455,105,15,1},
        {1,16,120,560,1820,4368,8008,11440,12870,11440,8008,4368,1820,560,120,16,1},
        {1,17,136,680,2380,6188,12376,19448,24310,24310,19448,12376,6188,2380,680,136,17,1},
        {1,18,153,816,3060,8568,18564,31824,43758,48620,43758,31824,18564,8568,3060,816,153,18,1},
        {1,19,171,969,3876,11628,27132,50388,75582,92378,92378,75582,50388,27132,11628,3876,969,171,19,1},
        {1,20,190,1140,4845,15504,38760,77520,125970,167960,184756,167960,125970,77520,38760,15504,4845,1140,190,20,1},
        {1,21,210,1330,5985,20349,54264,116280,203490,293930,352716,352716,293930,203490,116280,54264,20349,5985,1330,210,21,1},
        {1,22,231,1540,7315,26334,74613,170544,319770,497420,646646,705432,646646,497420,319770,170544,74613,26334,7315,1540,231,22,1},
        {1,23,253,1771,8855,33649,100947,245157,490314,817190,1144066,1352078,1352078,1144066,817190,490314,245157,100947,33649,8855,1771,253,23,1},
        {1,24,276,2024,10626,42504,134596,346104,735471,1307504,1961256,2496144,2704156,2496144,1961256,1307504,735471,346104,134596,42504,10626,2024,276,24,1},
        {1,25,300,2300,12650,53130,177100,480700,1081575,2042975,3268760,4457400,5200300,5200300,4457400,3268760,2042975,1081575,480700,177100,53130,12650,2300,300,25,1},
        {1,26,325,2600,14950,65780,230230,657800,1562275,3124550,5311735,7726160,9657700,10400600,9657700,7726160,5311735,3124550,1562275,657800,230230,65780,14950,2600,325,26,1},
        {1,27,351,2925,17550,80730,296010,888030,2220075,4686825,8436285,13037895,17383860,20058300,20058300,17383860,13037895,8436285,4686825,2220075,888030,296010,80730,17550,2925,351,27,1},
        {1,28,378,3276,20475,98280,376740,1184040,3108105,6906900,13123110,21474180,30421755,37442160,40116600,37442160,30421755,21474180,13123110,6906900,3108105,1184040,376740,98280,20475,3276,378,28,1},
        {1,29,406,3654,23751,118755,475020,1560780,4292145,10015005,20030010,34597290,51895935,67863915,77558760,77558760,67863915,51895935,34597290,20030010,10015005,4292145,1560780,475020,118755,23751,3654,406,29,1}};
        res.resize(numRows);
        return res;
    }

• _1021. 删除最外层的括号

//网络答案
    string removeOuterParentheses(string S) {
        string out="";
        int layer=0;
        for(int i=0;i<S.length();i++)
        {
            if(S[i]=='(')
                ++layer;
            if(layer!=1)
                out+=S[i];
            if(S[i]==')')
                --layer;
            
        }
        return out;
    }

• _71. 简化路径

//c语言
char* simplifyPath(char *path) {
    int length = 0;
    while (path[length] != '\0') {
        length++;
    }
    char *stack = (char *)malloc(sizeof(char) * (length + 2));
    int top = -1;
    stack[++top] = '/';
    for (int i = 0; i <= length; i++) {
        if (path[i] == '/' || (path[i] == '.' && (path[i + 1] == '/' || path[i + 1] == '\0'))) {
            continue;
        } else if (path[i] == '.' && path[i + 1] == '.' && (path[i + 2] == '/' || path [i + 2] == '\0')) {
            while (top > 0 && stack[--top] != '/');
            i++;
        } else {
            do {
                stack[++top] = path[i];
            } while(i < length && path[i] != '/' && ++i);
        }
    }
    if (top != 1 && stack[top - 1] == '/') {
        stack[--top] = '\0';
    }
    return stack;
}

• 旋转图像

方法三：用翻转代替旋转
我们还可以另辟蹊径，用翻转操作代替旋转操作。先将其通过水平轴翻转,再根据主对角线翻转,就得到了答案。这是为什么呢？对于水平轴翻转而言，我们只需要枚举矩阵上半部分的元素，和下半部分的元素进行交换，即对于主对角线翻转而言，我们只需要枚举对角线左侧的元素，和右侧的元素进行交换

• 比特位计数

    vector<int> countBits(int num) {
        vector<int> bits(num + 1);
        int highBit = 0;
        for (int i = 1; i <= num; i++) {
            if ((i & (i - 1)) == 0) {
                highBit = i;
            }
            bits[i] = bits[i - highBit] + 1;
        }
        return bits;
    }

• 268. 丢失的数字

//网络解答，集合
    int missingNumber(vector<int>& nums) {
        int ans=0;
        set<int>s(nums.begin(),nums.end());
        for(int i=0;i<=nums.size();i++)
            if(!s.count(i)) ans=i;
        return ans;
    }

• 931. 下降路径最小和

//网络解答，直接修改A，和处理边界这种思想很妙
    public int minFallingPathSum(int[][] A) {
        int N = A.length;
        for (int r = N-2; r >= 0; --r) {
            for (int c = 0; c < N; ++c) {
                // best = min(A[r+1][c-1], A[r+1][c], A[r+1][c+1])
                int best = A[r+1][c];
                if (c > 0)
                    best = Math.min(best, A[r+1][c-1]);
                if (c+1 < N)
                    best = Math.min(best, A[r+1][c+1]);
                A[r][c] += best;
            }
        }
        int ans = Integer.MAX_VALUE;
        for (int x: A[0])
            ans = Math.min(ans, x);
        return ans;
    }

• 1796. 字符串中第二大的数字

网络解答一

/*
利用 isdigit() 函数判断字符串中的数字部分;
利用set接收结果，自动去重;
全部接收后获得其中的最大值，移除该最大值；
判断集合是否为空，若为空则不存在第二大，直接输出-1；
若不为空，则再次取最大值，此值即为第二大的值；
*/
    int secondHighest(string s) {
        set<int>res;
        for(int i=0;i<s.size();i++){
            if(isdigit(s[i])) ///注意这个函数
            res.insert(s[i]-'0');
        }
        int max_num=*max_element(res.begin(),res.end());
        res.erase(max_num);
        if(res.size()==0) return -1;
        else 
        return *max_element(res.begin(),res.end());
    }

网络解答二，注意迭代器的使用

    int secondHighest(string s) 
    {   
        set<int> a;
        for (auto c: s)
        {
            if (isdigit(c) != 0)
                a.insert(c - '0');
        }
        if (a.size() < 2)
            return -1;
        
        auto it = a.rbegin();
        it ++;
        return *it;
    }

• 893. 特殊等价字符串组

网络解答

    int numSpecialEquivGroups(vector<string>& words) {
        int res=0;
        unordered_map<string , int> save;

        for(int i=0;i<words.size();i++){
            vector<int> count(52);        
            for(int j=0;j<words[i].length();j++){
                count[words[i][j]-'a'+(j%2)*26]++;
            }
            stringstream ss;
            string counS;
            copy(count.begin(), count.end(), ostream_iterator<int>(ss, ""));
            counS = ss.str();
            save[counS]=0;
        }
/*
        unordered_map::iterator it = save.begin();
        while(it != save.end()){
            cout<first<<" "<second<
        return save.size();
    }

• 387. 字符串中的第一个唯一字符

网络解答一

    int firstUniqChar(string s) {
        unordered_map<int, int> frequency;
        for (char ch: s) {
            ++frequency[ch];
        }
        for (int i = 0; i < s.size(); ++i) {
            if (frequency[s[i]] == 1) {
                return i;
            }
        }
        return -1;
    }

网络解答二

/*
*/
    int firstUniqChar(string s) {
        unordered_map<int, int> position;
        int n = s.size();
        for (int i = 0; i < n; ++i) {
            if (position.count(s[i])) {
                position[s[i]] = -1;
            }
            else {
                position[s[i]] = i;
            }
        }
        int first = n;
        for (auto [_, pos]: position) {
            if (pos != -1 && pos < first) {
                first = pos;
            }
        }
        if (first == n) {
            first = -1;
        }
        return first;
    }

网络解答三

/*
在维护队列时，我们使用了「延迟删除」这一技巧。
也就是说，即使队列中有一些字符出现了超过一次，但它只要不位于队首，
那么就不会对答案造成影响，我们也就可以不用去删除它。
只有当它前面的所有字符被移出队列，它成为队首时，我们才需要将它移除。
*/
    int firstUniqChar(string s) {
        unordered_map<char, int> position;
        queue<pair<char, int>> q;
        int n = s.size();
        for (int i = 0; i < n; ++i) {
            if (!position.count(s[i])) {
                position[s[i]] = i;
                q.emplace(s[i], i);
            }
            else {
                position[s[i]] = -1;
                while (!q.empty() && position[q.front().first] == -1) {
                    q.pop();
                }
            }
        }
        return q.empty() ? -1 : q.front().second;
    }

• 17. 电话号码的字母组合

简单解法

class Solution {
public:
    vector<string> letterCombinations(string digits) {
        vector<string> combinations;
        if (digits.empty()) {
            return combinations;
        }
        unordered_map<char, string> phoneMap{
            {'2', "abc"},
            {'3', "def"},
            {'4', "ghi"},
            {'5', "jkl"},
            {'6', "mno"},
            {'7', "pqrs"},
            {'8', "tuv"},
            {'9', "wxyz"}
        };
        string combination;
        backtrack(combinations, phoneMap, digits, 0, combination);
        return combinations;
    }

    void backtrack(vector<string>& combinations, const unordered_map<char, string>& phoneMap, const string& digits, int index, string& combination) {
        if (index == digits.length()) {
            combinations.push_back(combination);
        } else {
            char digit = digits[index];
            const string& letters = phoneMap.at(digit);
            for (const char& letter: letters) {
                combination.push_back(letter);
                backtrack(combinations, phoneMap, digits, index + 1, combination);
                combination.pop_back();
            }
        }
    }
};

2.不会做的题目

• *面试题 17.16. 按摩师 不会做

解题思路

求按摩师的最长预约时间，nums为按摩师的预约请求序列，求一个最优时间和，可以通过动态规划的方式来求，下面按照动态规划的步骤一步一步进行。
状态定义：

通过定义dp数组来记录最长时间 dp[i]为 0 到 i 的最长预约时间
状态转移方程：

对于dp[i]可以有两种状态，一种是接受当前预约，那么昨天肯定就不能预约，我们需要取得 i-2 天的时间加上当前的时间 dp[i-2] + nums[i]。
另一种就是不接受当前预约，那么就只取前一天的预约时间 i - 1 dp[i-1],我们需要求最大的时长 max(dp[i-1],dp[i-2]+nums[i])
状态初始化：

根据状态定义我们需要从i=2的位置开始计算，所以我们需要初始化0和1位置的时长，如果只有一天的话那么dp[0]这个位置我们必须要接受预约，如果有两天的话dp[1]的位置我们需要求两个时长的最大，所以dp[1] = Math.max(dp[0],nums[1]);
状态输出：

dp[len-1] 就是我们最终的状态。
看来动态规划的状态定义和转移方程 真的是需要不断的去练习。
代码

class Solution {
    public int massage(int[] nums) {
        int len  = nums.length;
        if(len == 0){
            return 0;
        }
        if(len == 1){
            return nums[0];
        }

        int[] dp = new int[len];
        dp[0] = nums[0];
        dp[1] = Math.max(dp[0],nums[1]);
        for(int i = 2; i < len;i++){
            dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i]);
        }
        return dp[len-1];
    }
}

//看答案后做的
class Solution {
public:
    int massage(vector<int>& nums) {
        if(nums.size()==0)
            return 0;
        if(nums.size()==1)
            return nums[0];
        
        int DP[nums.size()][2];
        DP[0][0] = 0;
        DP[0][1] = nums[0];
        DP[1][0] = nums[0];
        DP[1][1] = nums[1];
        for(int i=2;i<nums.size();i++)
        {
            DP[i][0] = max(DP[i-1][0],DP[i-1][1]);
            DP[i][1] = (DP[i-1][0])+nums[i];
        }
        return max(DP[nums.size()-1][0],DP[nums.size()-1][1]);
    }
};

• _714. 买卖股票的最佳时机含手续费

//不会做，网络答案
    int maxProfit(vector<int>& prices, int fee) {
        int n = prices.size();
        vector<int> f(2);
        // 0 : 不持股   1 : 持股
        f[0] = 0;
        f[1] = -prices[0];
        for(int i = 1; i<n; i++){
            f[0] = max(f[0], f[1] + prices[i] - fee);
            f[1] = max(f[1], f[0] - prices[i]);
        }
        return f[0];
    }

• _1047. 删除字符串中的所有相邻重复项
  题目描述：给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。在 S 上反复执行重复项删除操作，直到无法继续删除。在完成所有重复项删除操作后返回最终的字符串。输入：“abbaca”；输出：“ca”；

解法一：原地算法

    string removeDuplicates(string S) {
        int top = 0;
        for (char ch : S) {
            if (top == 0 || S[top - 1] != ch) {
                S[top++] = ch;
            } else {
                top--;
            }
        }
        S.resize(top);
        return S;
    }

解法二：C++ string 也能当栈用

    string removeDuplicates(string S) {
        string ret;
        for(auto c:S){
            if(ret.empty()||c!=ret.back()){
                ret.push_back(c);
            }else{
                ret.pop_back();
            }
        }
        return ret;
    }

解法三：空字符串哨兵

    def removeDuplicates(self, S: str) -> str:
        stack = [""]
        for ch in S:
            if ch == stack[-1]:
                stack.pop()
            else:
                stack.append(ch)
        return "".join(stack)

解法四：

//网络答案
    public String removeDuplicates(String S) {
        int now =S.length();
        int next = 1;
        while(now != next){
           now =  S.length();      S=S.replace("aa","").replace("bb","").replace("cc","").replace("dd","").replace("ee","").replace("ff","").replace("gg","").replace("hh","").replace("ii","").replace("jj","").replace("kk","").replace("ll","").replace("mm","").replace("nn","").replace("oo","").replace("pp","").replace("qq","").replace("rr","").replace("ss","").replace("tt","").replace("uu","").replace("vv","").replace("ww","").replace("xx","").replace("yy","").replace("zz","");
           next =  S.length();       
            }
        return S;
    }

• _516. 最长回文子序列 不会做

网络答案：动态规划

/*
解题思路：
状态
f[i][j] 表示 s 的第 i 个字符到第 j 个字符组成的子串中，最长的回文序列长度是多少。

转移方程
如果 s 的第 i 个字符和第 j 个字符相同的话
f[i][j] = f[i + 1][j - 1] + 2
如果 s 的第 i 个字符和第 j 个字符不同的话
f[i][j] = max(f[i + 1][j], f[i][j - 1])
然后注意遍历顺序，i 从最后一个字符开始往前遍历，j 从 i + 1 开始往后遍历，这样可以保证每个子问题都已经算好了。

初始化
f[i][i] = 1 单个字符的最长回文序列是 1

结果
f[0][n - 1]
*/
class Solution {
    public int longestPalindromeSubseq(String s) {
        int n = s.length();
        int[][] f = new int[n][n];
        for (int i = n - 1; i >= 0; i--) {
            f[i][i] = 1;
            for (int j = i + 1; j < n; j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    f[i][j] = f[i + 1][j - 1] + 2;
                } else {
                    f[i][j] = Math.max(f[i + 1][j], f[i][j - 1]);
                }
            }
        }
        return f[0][n - 1];
    }
}

五、赛码

https://www.acmcoder.com/index

六、技巧与结论总结

6.1 技巧总结

• 异或运算（XOR）满足结合律，并且对一个数进行两次完全相同的异或运算会得到原来的数，因此我们可以通过异或运算找到缺失的数字。
  例题：268. 丢失的数字官方答案方法三
• 调用C++自带的排序函数：sort(s.begin(), s.end());
  例题：242. 有效的字母异位词官方答案
• 对于回溯题目，引用相比参数传递能节省很大时间开销

6.2 结论总结

• 旋转矩阵
  假设矩阵边长为len，则操作的部分是：
  Row:[0,(len+1)/2]，Column:[0,len/2]，如下图所示
  
  

6.3 极端输入情况总结

笔试时看不到输入用例，因此无法根据不通过的结果调整代码，需要总结积累。

• 注意链表头节点为空的特殊情况

• 石子游戏
  题目：今天，度度熊和牛妹在玩取石子的游戏，开始的时候有堆石头，第堆有个石头，两个人轮流动作，度度熊先走，在每个回合，玩家选择一个非空堆，并从堆中移除一块石头。如果一个玩家在轮到他之前所有的石碓都是空的，或者如果在移动石头之后，存在两个堆包含相同数量的石头（可能为都为），那么他就会输。假设两人都在游戏时选择最佳方式，度度熊和牛妹谁会赢？如果度度熊获胜，输出“man”，如果牛妹获胜，输出“woman”（输出不包含双引号）。
  分析：先对数组排序，然后剔除特殊情况，之后轮流取直至变成0,1,2,3…形态。
  判断先手能否走第一步，以下情况不能：
  1）仅有一个数且为0；
  2）前两个数为0；
  3）如果一个数出现了3次；
  4）至少有2个数字出现两次；
  5）一个数字出现两次且其前一个数比他小一；

• 最小公倍数与最大公约数
  题目：度度熊请你找出两个数a,b，满足1<=a,b<=n，且lcm(a,b)-gcd(a,b)尽量大。输出最大的lcm(a,b)-gcd(a,b)。其中lcm(a,b)表示a和b的最小公倍数，gcd(a,b)表示a和b的最大公约数。
  结论：对于可能超出范围的情况，要使用范围更大的数据类型。

• 40. 组合总和 II
  用例一：
  [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
  27

• 212. 单词搜索 II
  遗漏情况：起始位置不是board[0][0];
  极端输入：
  [[“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”],[“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”],[“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”],[“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”],[“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”],[“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”],[“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”],[“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”],[“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”],[“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”,“a”,“b”]]
  [“ababababaa”,“ababababab”,“ababababac”,“ababababad”,“ababababae”,“ababababaf”,“ababababag”,“ababababah”,“ababababai”,“ababababaj”,“ababababak”,“ababababal”,“ababababam”,“ababababan”,“ababababao”,“ababababap”,“ababababaq”,“ababababar”,“ababababas”,“ababababat”,“ababababau”,“ababababav”,“ababababaw”,“ababababax”,“ababababay”,“ababababaz”,“ababababba”,“ababababbb”,“ababababbc”,“ababababbd”,“ababababbe”,“ababababbf”,“ababababbg”,“ababababbh”,“ababababbi”,“ababababbj”,“ababababbk”,“ababababbl”,“ababababbm”,“ababababbn”,“ababababbo”,“ababababbp”,“ababababbq”,“ababababbr”,“ababababbs”,“ababababbt”,“ababababbu”,“ababababbv”,“ababababbw”,“ababababbx”,“ababababby”,“ababababbz”,“ababababca”,“ababababcb”,“ababababcc”,“ababababcd”,“ababababce”,“ababababcf”,“ababababcg”,“ababababch”,“ababababci”,“ababababcj”,“ababababck”,“ababababcl”,“ababababcm”,“ababababcn”,“ababababco”,“ababababcp”,“ababababcq”,“ababababcr”,“ababababcs”,“ababababct”,“ababababcu”,“ababababcv”,“ababababcw”,“ababababcx”,“ababababcy”,“ababababcz”,“ababababda”,“ababababdb”,“ababababdc”,“ababababdd”,“ababababde”,“ababababdf”,“ababababdg”,“ababababdh”,“ababababdi”,“ababababdj”,“ababababdk”,“ababababdl”,“ababababdm”,“ababababdn”,“ababababdo”,“ababababdp”,“ababababdq”,“ababababdr”,“ababababds”,“ababababdt”,“ababababdu”,“ababababdv”,“ababababdw”,“ababababdx”,“ababababdy”,“ababababdz”,“ababababea”,“ababababeb”,“ababababec”,“ababababed”,“ababababee”,“ababababef”,“ababababeg”,“ababababeh”,“ababababei”,“ababababej”,“ababababek”,“ababababel”,“ababababem”,“ababababen”,“ababababeo”,“ababababep”,“ababababeq”,“ababababer”,“ababababes”,“ababababet”,“ababababeu”,“ababababev”,“ababababew”,“ababababex”,“ababababey”,“ababababez”,“ababababfa”,“ababababfb”,“ababababfc”,“ababababfd”,“ababababfe”,“ababababff”,“ababababfg”,“ababababfh”,“ababababfi”,“ababababfj”,“ababababfk”,“ababababfl”,“ababababfm”,“ababababfn”,“ababababfo”,“ababababfp”,“ababababfq”,“ababababfr”,“ababababfs”,“ababababft”,“ababababfu”,“ababababfv”,“ababababfw”,“ababababfx”,“ababababfy”,“ababababfz”,“ababababga”,“ababababgb”,“ababababgc”,“ababababgd”,“ababababge”,“ababababgf”,“ababababgg”,“ababababgh”,“ababababgi”,“ababababgj”,“ababababgk”,“ababababgl”,“ababababgm”,“ababababgn”,“ababababgo”,“ababababgp”,“ababababgq”,“ababababgr”,“ababababgs”,“ababababgt”,“ababababgu”,“ababababgv”,“ababababgw”,“ababababgx”,“ababababgy”,“ababababgz”,“ababababha”,“ababababhb”,“ababababhc”,“ababababhd”,“ababababhe”,“ababababhf”,“ababababhg”,“ababababhh”,“ababababhi”,“ababababhj”,“ababababhk”,“ababababhl”,“ababababhm”,“ababababhn”,“ababababho”,“ababababhp”,“ababababhq”,“ababababhr”,“ababababhs”,“ababababht”,“ababababhu”,“ababababhv”,“ababababhw”,“ababababhx”,“ababababhy”,“ababababhz”,“ababababia”,“ababababib”,“ababababic”,“ababababid”,“ababababie”,“ababababif”,“ababababig”,“ababababih”,“ababababii”,“ababababij”,“ababababik”,“ababababil”,“ababababim”,“ababababin”,“ababababio”,“ababababip”,“ababababiq”,“ababababir”,“ababababis”,“ababababit”,“ababababiu”,“ababababiv”,“ababababiw”,“ababababix”,“ababababiy”,“ababababiz”,“ababababja”,“ababababjb”,“ababababjc”,“ababababjd”,“ababababje”,“ababababjf”,“ababababjg”,“ababababjh”,“ababababji”,“ababababjj”,“ababababjk”,“ababababjl”,“ababababjm”,“ababababjn”,“ababababjo”,“ababababjp”,“ababababjq”,“ababababjr”,“ababababjs”,“ababababjt”,“ababababju”,“ababababjv”,“ababababjw”,“ababababjx”,“ababababjy”,“ababababjz”,“ababababka”,“ababababkb”,“ababababkc”,“ababababkd”,“ababababke”,“ababababkf”,“ababababkg”,“ababababkh”,“ababababki”,“ababababkj”,“ababababkk”,“ababababkl”,“ababababkm”,“ababababkn”,“ababababko”,“ababababkp”,“ababababkq”,“ababababkr”,“ababababks”,“ababababkt”,“ababababku”,“ababababkv”,“ababababkw”,“ababababkx”,“ababababky”,“ababababkz”,“ababababla”,“abababablb”,“abababablc”,“ababababld”,“abababable”,“abababablf”,“abababablg”,“abababablh”,“ababababli”,“abababablj”,“abababablk”,“ababababll”,“abababablm”,“ababababln”,“abababablo”,“abababablp”,“abababablq”,“abababablr”,“ababababls”,“abababablt”,“abababablu”,“abababablv”,“abababablw”,“abababablx”,“abababably”,“abababablz”,“ababababma”,“ababababmb”,“ababababmc”,“ababababmd”,“ababababme”,“ababababmf”,“ababababmg”,“ababababmh”,“ababababmi”,“ababababmj”,“ababababmk”,“ababababml”,“ababababmm”,“ababababmn”,“ababababmo”,“ababababmp”,“ababababmq”,“ababababmr”,“ababababms”,“ababababmt”,“ababababmu”,“ababababmv”,“ababababmw”,“ababababmx”,“ababababmy”,“ababababmz”,“ababababna”,“ababababnb”,“ababababnc”,“ababababnd”,“ababababne”,“ababababnf”,“ababababng”,“ababababnh”,“ababababni”,“ababababnj”,“ababababnk”,“ababababnl”,“ababababnm”,“ababababnn”,“ababababno”,“ababababnp”,“ababababnq”,“ababababnr”,“ababababns”,“ababababnt”,“ababababnu”,“ababababnv”,“ababababnw”,“ababababnx”,“ababababny”,“ababababnz”,“ababababoa”,“ababababob”,“ababababoc”,“ababababod”,“ababababoe”,“ababababof”,“ababababog”,“ababababoh”,“ababababoi”,“ababababoj”,“ababababok”,“ababababol”,“ababababom”,“ababababon”,“ababababoo”,“ababababop”,“ababababoq”,“ababababor”,“ababababos”,“ababababot”,“ababababou”,“ababababov”,“ababababow”,“ababababox”,“ababababoy”,“ababababoz”,“ababababpa”,“ababababpb”,“ababababpc”,“ababababpd”,“ababababpe”,“ababababpf”,“ababababpg”,“ababababph”,“ababababpi”,“ababababpj”,“ababababpk”,“ababababpl”,“ababababpm”,“ababababpn”,“ababababpo”,“ababababpp”,“ababababpq”,“ababababpr”,“ababababps”,“ababababpt”,“ababababpu”,“ababababpv”,“ababababpw”,“ababababpx”,“ababababpy”,“ababababpz”,“ababababqa”,“ababababqb”,“ababababqc”,“ababababqd”,“ababababqe”,“ababababqf”,“ababababqg”,“ababababqh”,“ababababqi”,“ababababqj”,“ababababqk”,“ababababql”,“ababababqm”,“ababababqn”,“ababababqo”,“ababababqp”,“ababababqq”,“ababababqr”,“ababababqs”,“ababababqt”,“ababababqu”,“ababababqv”,“ababababqw”,“ababababqx”,“ababababqy”,“ababababqz”,“ababababra”,“ababababrb”,“ababababrc”,“ababababrd”,“ababababre”,“ababababrf”,“ababababrg”,“ababababrh”,“ababababri”,“ababababrj”,“ababababrk”,“ababababrl”,“ababababrm”,“ababababrn”,“ababababro”,“ababababrp”,“ababababrq”,“ababababrr”,“ababababrs”,“ababababrt”,“ababababru”,“ababababrv”,“ababababrw”,“ababababrx”,“ababababry”,“ababababrz”,“ababababsa”,“ababababsb”,“ababababsc”,“ababababsd”,“ababababse”,“ababababsf”,“ababababsg”,“ababababsh”,“ababababsi”,“ababababsj”,“ababababsk”,“ababababsl”,“ababababsm”,“ababababsn”,“ababababso”,“ababababsp”,“ababababsq”,“ababababsr”,“ababababss”,“ababababst”,“ababababsu”,“ababababsv”,“ababababsw”,“ababababsx”,“ababababsy”,“ababababsz”,“ababababta”,“ababababtb”,“ababababtc”,“ababababtd”,“ababababte”,“ababababtf”,“ababababtg”,“ababababth”,“ababababti”,“ababababtj”,“ababababtk”,“ababababtl”,“ababababtm”,“ababababtn”,“ababababto”,“ababababtp”,“ababababtq”,“ababababtr”,“ababababts”,“ababababtt”,“ababababtu”,“ababababtv”,“ababababtw”,“ababababtx”,“ababababty”,“ababababtz”,“ababababua”,“ababababub”,“ababababuc”,“ababababud”,“ababababue”,“ababababuf”,“ababababug”,“ababababuh”,“ababababui”,“ababababuj”,“ababababuk”,“ababababul”,“ababababum”,“ababababun”,“ababababuo”,“ababababup”,“ababababuq”,“ababababur”,“ababababus”,“ababababut”,“ababababuu”,“ababababuv”,“ababababuw”,“ababababux”,“ababababuy”,“ababababuz”,“ababababva”,“ababababvb”,“ababababvc”,“ababababvd”,“ababababve”,“ababababvf”,“ababababvg”,“ababababvh”,“ababababvi”,“ababababvj”,“ababababvk”,“ababababvl”,“ababababvm”,“ababababvn”,“ababababvo”,“ababababvp”,“ababababvq”,“ababababvr”,“ababababvs”,“ababababvt”,“ababababvu”,“ababababvv”,“ababababvw”,“ababababvx”,“ababababvy”,“ababababvz”,“ababababwa”,“ababababwb”,“ababababwc”,“ababababwd”,“ababababwe”,“ababababwf”,“ababababwg”,“ababababwh”,“ababababwi”,“ababababwj”,“ababababwk”,“ababababwl”,“ababababwm”,“ababababwn”,“ababababwo”,“ababababwp”,“ababababwq”,“ababababwr”,“ababababws”,“ababababwt”,“ababababwu”,“ababababwv”,“ababababww”,“ababababwx”,“ababababwy”,“ababababwz”,“ababababxa”,“ababababxb”,“ababababxc”,“ababababxd”,“ababababxe”,“ababababxf”,“ababababxg”,“ababababxh”,“ababababxi”,“ababababxj”,“ababababxk”,“ababababxl”,“ababababxm”,“ababababxn”,“ababababxo”,“ababababxp”,“ababababxq”,“ababababxr”,“ababababxs”,“ababababxt”,“ababababxu”,“ababababxv”,“ababababxw”,“ababababxx”,“ababababxy”,“ababababxz”,“ababababya”,“ababababyb”,“ababababyc”,“ababababyd”,“ababababye”,“ababababyf”,“ababababyg”,“ababababyh”,“ababababyi”,“ababababyj”,“ababababyk”,“ababababyl”,“ababababym”,“ababababyn”,“ababababyo”,“ababababyp”,“ababababyq”,“ababababyr”,“ababababys”,“ababababyt”,“ababababyu”,“ababababyv”,“ababababyw”,“ababababyx”,“ababababyy”,“ababababyz”,“ababababza”,“ababababzb”,“ababababzc”,“ababababzd”,“ababababze”,“ababababzf”,“ababababzg”,“ababababzh”,“ababababzi”,“ababababzj”,“ababababzk”,“ababababzl”,“ababababzm”,“ababababzn”,“ababababzo”,“ababababzp”,“ababababzq”,“ababababzr”,“ababababzs”,“ababababzt”,“ababababzu”,“ababababzv”,“ababababzw”,“ababababzx”,“ababababzy”,“ababababzz”]

6.4 模板总结

表格内单词搜索（）：

七、刷题分类

1.动态规划

「滚动数组思想」是一种常见的动态规划优化方法，在我们的题目中已经多次使用到，例如「剑指 Offer 46. 把数字翻译成字符串」、「70. 爬楼梯」等，当我们定义的状态在动态规划的转移方程中只和某几个状态相关的时候，就可以考虑这种优化方法，目的是给空间复杂度「降维」。如果你还不知道什么是「滚动数组思想」，一定要查阅相关资料进行学习哦。
回顾这道题，其实这类动态规划的题目在题库中也出现过多次，例如「221. 最大正方形」、「1162. 地图分析」等。他们都以二维坐标作为状态，大多数都可以使用滚动数组进行优化。如果我们熟悉这类问题，可以一眼看出这是一个动态规划问题。当我们不熟悉的时候，怎么想到用动态规划来解决这个问题呢？我们需要从问题本身出发，寻找一些有用的信息，例如本题中：

(i,j)(i, j)(i,j) 位置只能从 (i−1,j)(i - 1, j)(i−1,j) 和 (i,j−1)(i, j - 1)(i,j−1) 走到，这样的条件就是在告诉我们这里转移是 「无后效性」 的，f(i,j)f(i, j)f(i,j) 和任何的 f(i′,j′)(i′>i,j′>j)f(i', j')(i' > i, j' > j)f(i′,j′)(i′>i,j′>j) 无关。
动态规划的题目分为两大类，一种是求最优解类，典型问题是背包问题，另一种就是计数类，比如这里的统计方案数的问题，它们都存在一定的递推性质。前者的递推性质还有一个名字，叫做 「最优子结构」 ——即当前问题的最优解取决于子问题的最优解，后者类似，当前问题的方案数取决于子问题的方案数。所以在遇到求方案数的问题时，我们可以往动态规划的方向考虑。

通常如果我们察觉到了这两点要素，这个问题八成可以用动态规划来解决。读者可以多多练习，熟能生巧。

2.分治算法

• 摩尔投票法（参考例题官方解答三：剑指 Offer 39. 数组中出现次数超过一半的数字）

3.回溯

• 网络总结
  C++在做递归回溯算法相关题目时，递归函数形参传值和传引用运行速度有很大的差异。这是我这道题dfs函数的声明，主要区别是visited和word，一个是传值，一个是传引用。前者执行超时，后者在本题是32ms.
  个人理解为传值时每次递归调用都要在内存中新建立一个vector 来保存visit传入的值，但是传引用直接在visited原始位置操作，不需要进行新建变量与赋值，节省了代码运行的空间与时间开销。
  参见：79. 单词搜索

八、基本语法

• 对于vector变量，直接使用时，下标表示对应元素，使用一些函数时应该用其指针（迭代器），而不是下标

//正确书写
PaiLie.erase(PaiLie.begin()+k);
//错误书写
PaiLie.erase(k);

//正确书写
PaiLie.insert(PaiLie.begin()+iPL, cur);
//错误书写
PaiLie.insert(iPL, cur);

• 对指针指向的变量进行操作要加括号

（*pNum） ++;

九、复习进度与总结

JZ offer

• 1
  错误注意：
  1.越界，j>=n,i<0；
  2.让起始位置从左下角或者右上角开始
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
  注意：是f(n-1)+f(n-2)而不是f(n-1)+2*f(n-2)
• 11
• 12
• 13
• 14
  错误注意：是要把前面所有的加起来，循环里需要再套循环；

JZ1

十、错误原因解析

• 错误一
  错误描述：运行错误:请检查是否存在数组、列表等越界非法访问，内存非法访问等情况
• 错误二
  错误描述：段错误:您的程序发生段错误，可能是数组越界，堆栈溢出（比如，递归调用层数太多）等情况引起。
  可能原因：
  1.递归无法结束，循环无法结束；
  2.遇到输入数据量为零的情况没有直接返回。
• 错误三
  错误描述：In file included from main.cc:2: ./solution.h:39:5: error: non-void function does not return a value in all control paths [-Werror,-Wreturn-type]
  可能原因：
  1.“not all control paths return a value”， 这句话的意思是函数并不是所有分支都有返回值，所以需要增加判断并返回相应值；或增加总的返回值。
• 错误四
  错误描述：runtime error: member access within null pointer of type ‘TreeNode’
  错误解释：运行时错误:'TreeNode’类型的空指针中的成员访问。
  解决方案：出现这种问题是访问了空指针的成员，在前面用if语句判断指针是否为空即可。
• 错误五
  错误描述：AddressSanitizer:DEADLYSIGNAL43ERROR: AddressSanitizer: stack-overflow on address 0x7ffd4beabff8 (pc 0x00000034a876 bp 0x7ffd4beac010 sp 0x7ffd4beac000 T0)
  43ABORTING
• 错误六
  错误描述：Line 5: Char 17: runtime error: variable length array bound evaluates to non-positive value 0
  解决方案：数组长度定义为了负数，不正确。

---

总结

无
三道题套路解决递归问题