平衡2叉树堆搜索树

---

剑指offer40.最小的k个数

添加链接描述
最大堆， priority_queue 优先级队列进行处理（底层 原理类似堆）.现在使用现成的解决方案。如果需要了解堆实现，可以自行了解一下 //最大堆（大根堆）：树中每个非叶子结点大于等于其左右孩子结点的值，根节点最大的堆

void AdjustDown(int* a, int n, int root)
{	int parent = root;
	int child = parent * 2 + 1; // 左孩子
	while (child < n)
	{		// 找出左右孩子中大的那一个
		if (child+1 < n && a[child + 1] >a[child])//child+1 < n ：只有右孩子
		{			++child;
		}

		// 如果孩子小于父亲则交换
		if (a[child] >a[parent])
		{			int tmp = a[child];
	a[child] = a[parent];
	a[parent]= tmp;
			parent = child;//迭代
			child = parent * 2 + 1;
		}
		else
		{			break;
		}
	}
}
int* getLeastNumbers(int* arr, int arrSize, int k, int* returnSize){
*returnSize = k;
int* retArr = (int*)malloc(sizeof(int)*k);
if(k == 0)//返回最小的0个数
return retArr;//返回空数组
for( int i = 0; i < k; ++i){
retArr[i] = arr[i];//取数组中的前k个数构建一个大堆
}
//建k个数的大堆，倒数的第一个非叶子节点的子树开始
for(int i = (k-1-1)/2; i >= 0; --i){
AdjustDown ( retArr, k, i);
}//大堆就已经构建完成了，前k个数中最大的数就在堆顶，而小的数都在最下面
//只有最小的前k个才能进了堆
//除了那K个数剩下的数:
for(int j = k; j < arrSize; ++j){
if(arr[j] < retArr[0]){//没有进入堆的数去和堆顶比较（直接把大的数替换掉），retArr[0]=堆顶的数据直接被覆盖掉,
retArr[0] = arr[j];
AdjustDown ( retArr, k, 0);}}
//现在 大堆就是一个最小的前k个数所构建的大堆，堆顶就是最大的数
return retArr;}

struct comp{排序规则
	bool operator()(const int &a, const int &b){
		return a < b; //大堆，降序排序
	} };
class Solution {
public: vector<int> 
		GetLeastNumbers_Solution(vector<int> input, int k) 
{ vector<int> list;
		if(input.size() == 0 || k <= 0 || k > input.size())
		{ return list; }
priority_queue<int, vector<int>, comp> queue; //采用指定容器实现最大堆 
		for(int i = 0; i < input.size(); i++)
		{ if( i < k){ //前k个元素，直接放入，priority_queue内部会降序排序
				queue.push(input[i]); }
			else
			{
				if(input[i] < queue.top()){
//新的数据，小于queue首部元素（最大值）
				queue.pop(); 拿走max
				queue.push(input[i]);插入新数据，priority_queue内部的值又会自动排序
				}
			}
		}
		for(int i = 0; i < k; i++)
		{ list.push_back(queue.top());
		queue.pop(); }
		return list;
}
};

哈夫曼树

基础介绍
11 8 6 2 5构造哈夫曼树：

平衡2叉树

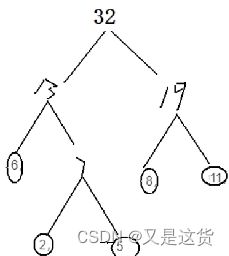
若将关键字1，2。3，4，5，6，7依次插入到初始为空的平衡二叉树T中，则T中平衡因子为0的分支结点的个数是3个：节点4、节点2、节点6

因为树、图的产生是递归式的，所以解决树、图的方法：递归、分治

606. 根据二叉树创建字符串

前序遍历的方式，将一个二叉树转换成一个由括号和整数组成的字符串。
空节点则用一对空括号 “()” 表示。省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

使用string优点：1自动增容2不需要找尾，自己记录尾
有大量深拷贝，每次递归调用tree2str会创建1个string，每个string会return s传值返回，要拷贝构造s，再把原来的释放，string越大拷贝构造代价越大
尽量不要定义全局变量，多线程时，可能2个人同时在改这1个变量，有安全问题

class Solution {
public:
    string tree2str(TreeNode*root) {
	string s;//定义空对象
	if (root == nullptr)
		return s;//返回匿名对象，空字符串
	s += to_string(root->val);//根
//把int的val转为字符串，string的+运算的对象只能是char string，
	if (root->left == nullptr && root->right == nullptr)
		return s;
//如示例2中数字3的左右子树都是空，只返回数字3
	s += '(';
//根走完加（，左树走完加）,把左右子树用括号括起来
	s += tree2str(root->left);//递归左树
	s += ')';
	if (root->right != nullptr)
	{
		s += '(';
		s += tree2str(root->right);//递归右树
		s += ')';
	}
	return s;
}
};

搜索树的第k个节点

添加链接描述
BST本身就是有序的，中序遍历：升序， 第k小，即中序遍历时到达第k个元素(二叉搜索树，不存在两个相同的节点值) ，循环中序遍历：非递归

TreeNode* KthNode(TreeNode* pRoot, int k) { 第k个，从k开始 
	if(pRoot == nullptr || k <= 0)
	{ return nullptr; }
	stack<TreeNode*> st;
	TreeNode *node = pRoot; 
do
{
	while(node != nullptr)
	{ //左子树全部入栈 
		st.push(node);
		node = node->left; 
	}
	if(!st.empty())开始访问左子树
	{ node = st.top(); 
		st.pop();
		k--; 
		if(k == 0)
		{ return node; 	//找到了该节点 
		}
		node = node->right; 
	}
}node：当前访问的节点，st:历史上曾经访问过
	while(node != nullptr || !st.empty()); 
//node有可能为空，但是只要stack不为空，就要继续pop求下一个。有没有可能st为空？有可能，这个时候就 要检测node，如果node不为空，就要整体检测右子树 
return nullptr;//树里没有要的这个值
 }

中序：2345678

JZ36 搜索树与双向链表

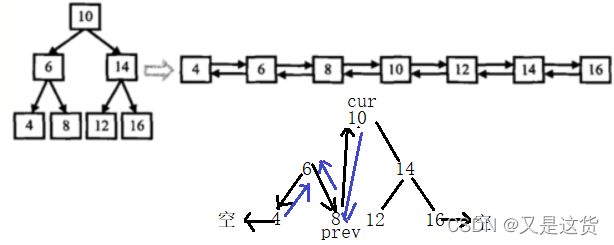
二叉搜索树转换成一个排序的双向链表

class Solution {
public:
    void _Convert(TreeNode* cur, TreeNode* & prev)
//每1层传下去都是上一层的引用&，最终栈帧中只有1个prev
{ if(cur == NULL)
 return;//递归，中序,left类比做链表prev,right类比做链表next
//cur知道自己的前1个是谁，但不知道后1个是谁
_Convert(cur->left, prev);
cur->left = prev;
if(prev)
prev->right= cur;
prev =cur;
_Convert(cur->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
	if (pRootOfTree == NULL)
		return NULL;
	TreeNode* prev = nullptr;
	_Convert(pRootOfTree, prev);
	TreeNode* head = pRootOfTree;
	while (head->left)
	{
		head = head->left;
	}
	return head;
}
};

将关键字1，2，3，4，5，6，7依次插入到初始为空的平衡二叉树T中，则T中平衡因子为0的分支结点(不包括)的个数是:3

236最近公共祖先

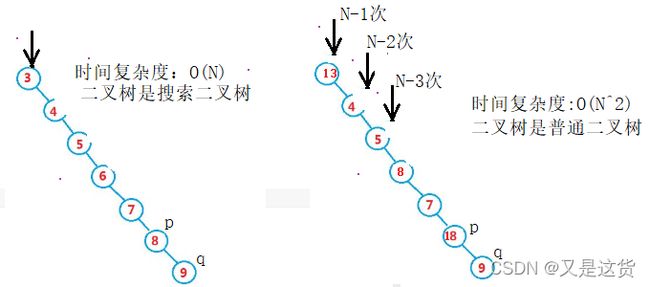
时间复杂度：O(n^2):

class Solution {
public:
    bool TreeFind(TreeNode*root,TreeNode*x)
{
	if (root == NULL)
		return false;
	if (root == x)
		return true;
	return TreeFind(root->left,x) || TreeFind(root->right,x);
}
TreeNode* lowestCommonAncestor(TreeNode*root,TreeNode* p,TreeNode*q){
//传节点指针TreeNode* p，不能传值，树里有相同的值时,有误导
	if (root == nullptr)
		return nullptr;
	if (p == root || q == root){
		return root; }
	bool pInLeft, pInRight, qInLeft, qInRight;
	pInLeft = TreeFind(root->left,p);
	pInRight = !pInLeft;
	qInLeft = TreeFind(root->left,q);
	qInRight = !qInLeft;
	//if：P或者q在左，q或者p在右，root就是最近公共祖先
	// else if：q p都在左 qInLeft pInLeft，去左边找祖先
	//else：q p都在右 qInRight pInRight，去右边找祖先
	if ((pInLeft &&qInRight) || (pInRight && qInLeft))
		return root;
	else if (pInLeft && qInLeft)
		return lowestCommonAncestor(root->left, p, q);
	else
		return lowestCommonAncestor(root->right,p, q);
}   
    };

时间复杂度：O(n):

class Solution {
public:
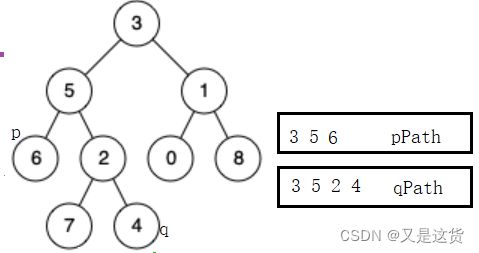
bool FindPath(TreeNode*root,TreeNode* x, stack<TreeNode*>& path)
{//在树中找出根到x的路径，前序遍历找路径
	if (root == NULL)
		return false;
	path.push(root);
	if (root == x)
		return true;
	if (FindPath(root->left, x, path))//递归到左边去找
		return true;
	if (FindPath(root->right, x, path))
		return true;
	//root root左树 root右树，都没有x节点,说明root不会是路径中一个节点，所以弹出
	path.pop();
	return false;
}
TreeNode* lowestCommonAncestor(TreeNode*root,TreeNode* p,TreeNode*q){
	stack<TreeNode*> pPath;//stack里存节点指针
	stack<TreeNode*> qPath;
	FindPath(root,p, pPath);
	FindPath(root, q, qPath);
	while (pPath.size() > qPath.size()){
		pPath.pop();//相当于链表相交题里长链表先走gap步
	}
	while (pPath.size() < qPath.size()){
		qPath.pop();
	}
	while (pPath.top() != qPath.top())
	{
		pPath.pop();
		qPath.pop();
	}
	return pPath.top();//此时相当于链表相交
}
    };

二叉树的节点有没有parent 时，可以和类比链表相交的题

学习的过程不要把自己当成天赋很高的人，递归不出来就画图，会有情绪，别人不画图做出了就是理解了递归，你不画图做不出来说明你还是没理解，画图、代码没有别人多，

最近公共祖先

class LCA {
public:
	int getLCA(int a, int b){
		while (a != b){较大的找到父节点：
			if (a >b){
				a =a / 2; }
			else {
				b = b / 2;		
			}
		}return a;
	}
};

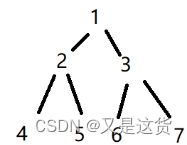
若a=7,b=2,过程：7>2,7的父亲=3！=2；3>2,3的父亲=1！=2；2>1,2的父亲=1=1,结束循环
—棵完全二叉树第六层有9个叶结点(根为第一层)，则结点个数最多有：
7层满2叉树的总节点-第6层的9个节点没有左右孩子的个数=结果
2^7 - 1 = 127,127-9*2=127-18=109