基于Softmax回归的多分类任务
Logistic回归可以有效地解决二分类问题,但在分类任务中,还有一类多分类问题,即类别数C大于2 的分类问题。Softmax回归就是Logistic回归在多分类问题上的推广。
使用Softmax回归模型对一个简单的数据集进行多分类实验。
首先给大家看一下需要的资源包
代码最后都会放出。
1.数据集的构建
我们首先构建一个简单的多分类任务,并构建训练集、验证集和测试集。
本任务的数据来自3个不同的簇,每个簇对一个类别。我们采集1000条样本,每个样本包含2个特征。
数据集的构建函数make_multiclass_classification的代码实现如下:
def make_multiclass_classification(n_samples=100, n_features=2, n_classes=3, shuffle=True, noise=0.1):
"""
生成带噪音的多类别数据
输入:
- n_samples:数据量大小,数据类型为int
- n_features:特征数量,数据类型为int
- shuffle:是否打乱数据,数据类型为bool
- noise:以多大的程度增加噪声,数据类型为None或float,noise为None时表示不增加噪声
输出:
- X:特征数据,shape=[n_samples,2]
- y:标签数据, shape=[n_samples,1]
"""
# 计算每个类别的样本数量
n_samples_per_class = [int(n_samples / n_classes) for k in range(n_classes)]
for i in range(n_samples - sum(n_samples_per_class)):
n_samples_per_class[i % n_classes] += 1
# 将特征和标签初始化为0
X = torch.zeros((n_samples, n_features))
y = torch.zeros(n_samples, dtype=torch.int32)
# 随机生成3个簇中心作为类别中心
centroids = torch.randperm(2 ** n_features)[:n_classes]
centroids_bin = np.unpackbits(centroids.numpy().astype('uint8')).reshape((-1, 8))[:, -n_features:]
centroids = torch.tensor(centroids_bin, dtype=torch.float32)
# 控制簇中心的分离程度
centroids = 1.5 * centroids - 1
# 随机生成特征值
X[:, :n_features] = torch.randn((n_samples, n_features))
stop = 0
# 将每个类的特征值控制在簇中心附近
for k, centroid in enumerate(centroids):
start, stop = stop, stop + n_samples_per_class[k]
# 指定标签值
y[start:stop] = k % n_classes
X_k = X[start:stop, :n_features]
# 控制每个类别特征值的分散程度
A = 2 * torch.rand(size=(n_features, n_features)) - 1
X_k[...] = torch.matmul(X_k, A)
X_k += centroid
X[start:stop, :n_features] = X_k
# 如果noise不为None,则给特征加入噪声
if noise > 0.0:
# 生成noise掩膜,用来指定给那些样本加入噪声
noise_mask = torch.rand(n_samples) < noise
for i in range(len(noise_mask)):
if noise_mask[i]:
# 给加噪声的样本随机赋标签值
y[i] = torch.randint(n_classes, size=(1,), dtype=torch.int32)
# 如果shuffle为True,将所有数据打乱
if shuffle:
idx = torch.randperm(X.shape[0])
X = X[idx]
y = y[idx]
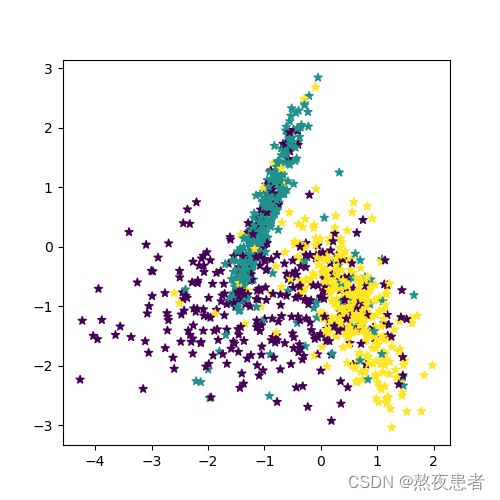
return X, y随机采集1000个样本,并进行可视化。
# 采样1000个样本
n_samples = 1000
X, y = make_multiclass_classification(n_samples=n_samples, n_features=2, n_classes=3, noise=0.2)
# 可视化生产的数据集,不同颜色代表不同类别
plt.figure(figsize=(5,5))
plt.scatter(x=X[:, 0].tolist(), y=X[:, 1].tolist(), marker='*', c=y.tolist())
plt.savefig('linear-dataset-vis2.pdf')
plt.show()
运行结果如下:
将实验数据拆分成训练集、验证集和测试集。其中训练集640条、验证集160条、测试集200条。
num_train = 640
num_dev = 160
num_test = 200
X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]
# 打印X_train和y_train的维度
print("X_train shape: ", X_train.shape, "y_train shape: ", y_train.shape)这样,我们就完成了Multi1000数据集的构建。
# 打印前5个数据的标签
print(y_train[:5])运行结果如下:
2.模型构建
在Softmax回归中,对类别进行预测的方式是预测输入属于每个类别的条件概率。与Logistic 回归不同的是,Softmax回归的输出值个数等于类别数C,而每个类别的概率值则通过Softmax函数进行求解。
softmax函数
Softmax函数可以将多个标量映射为一个概率分布。对于一个![]() 维向量,
维向量,![]() ,Softmax的计算公式为
,Softmax的计算公式为
在Softmax函数的计算过程中,要注意上溢出和下溢出的问题。假设Softmax 函数中所有的![]() 都是相同大小的数值
都是相同大小的数值![]() ,理论上,所有的输出都应该为
,理论上,所有的输出都应该为![]() 。但需要考虑如下两种特殊情况:
。但需要考虑如下两种特殊情况:
 为一个非常大的负数,此时
为一个非常大的负数,此时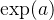 会发生下溢出现象。计算机在进行数值计算时,当数值过小,会被四舍五入为0。此时,Softmax函数的分母会变为0,导致计算出现问题;
会发生下溢出现象。计算机在进行数值计算时,当数值过小,会被四舍五入为0。此时,Softmax函数的分母会变为0,导致计算出现问题; 为一个非常大的正数,此时会导致
为一个非常大的正数,此时会导致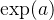 发生上溢出现象,导致计算出现问题。
发生上溢出现象,导致计算出现问题。
为了解决上溢出和下溢出的问题,在计算Softmax函数时,可以使用![]() 代替
代替![]() 。 此时,通过减去最大值,
。 此时,通过减去最大值,![]() 最大为0,避免了上溢出的问题;同时,分母中至少会包含一个值为1的项,从而也避免了下溢出的问题。
最大为0,避免了上溢出的问题;同时,分母中至少会包含一个值为1的项,从而也避免了下溢出的问题。
Softmax函数的代码实现如下(activation.py):
# x为tensor
def softmax(X):
"""
输入:
- X:shape=[N, C],N为向量数量,C为向量维度
"""
x_max = paddle.max(X, axis=1, keepdim=True)#N,1
x_exp = paddle.exp(X - x_max)
partition = paddle.sum(x_exp, axis=1, keepdim=True)#N,1
return x_exp / partition
# 观察softmax的计算方式
X = paddle.to_tensor([[0.1, 0.2, 0.3, 0.4],[1,2,3,4]])
predict = softmax(X)
print(predict)运行结果如下:
soft回归算子
在Softmax回归中,类别标签![]() 。给定一个样本
。给定一个样本![]() ,使用Softmax回归预测的属于类别
,使用Softmax回归预测的属于类别![]() 的条件概率为
的条件概率为
![]()
其中![]() 是第
是第![]() 类的权重向量,
类的权重向量,![]() 是第c类的偏置。
是第c类的偏置。
Softmax回归模型其实就是线性模型与softmax函数的组合。
将N个样本归为一组进行成批的预测。
![]()
其中![]() 为N个样本的特征矩阵,
为N个样本的特征矩阵,![]() 为
为![]() 个类的权重向量组成的矩阵,
个类的权重向量组成的矩阵,![]() 为所有类别的预测条件概率组成的矩阵。
为所有类别的预测条件概率组成的矩阵。
我们根据公式(3.13)实现Softmax回归算子,代码实现如下:
class model_SR(Op):
def __init__(self, input_dim, output_dim):
super(model_SR, self).__init__()
self.params = {}
#将线性层的权重参数全部初始化为0
self.params['W'] = torch.zeros((input_dim, output_dim))
#self.params['W'] = paddle.normal(mean=0, std=0.01, shape=[input_dim, output_dim])
#将线性层的偏置参数初始化为0
self.params['b'] = torch.zeros(output_dim)
#存放参数的梯度
self.grads = {}
self.X = None
self.outputs = None
self.output_dim = output_dim
def __call__(self, inputs):
return self.forward(inputs)
def forward(self, inputs):
self.X = inputs
#线性计算
score = torch.matmul(self.X, self.params['W']) + self.params['b']
#Softmax 函数
self.outputs = softmax(score)
return self.outputs
# 随机生成1条长度为4的数据
inputs = paddle.randn(shape=[1,4])
print('Input is:', inputs)
# 实例化模型,这里令输入长度为4,输出类别数为3
model = model_SR(input_dim=4, output_dim=3)
outputs = model(inputs)
print('Output is:', outputs)从输出结果可以看出,采用全0初始化后,属于每个类别的条件概率均为![]() 。这是因为,不论输入值的大小为多少,线性函数
。这是因为,不论输入值的大小为多少,线性函数![]() 的输出值恒为0。此时,再经过Softmax函数的处理,每个类别的条件概率恒等。
的输出值恒为0。此时,再经过Softmax函数的处理,每个类别的条件概率恒等。
3.损失函数
Softmax回归同样使用交叉熵损失作为损失函数,并使用梯度下降法对参数进行优化。通常使用![]() 维的one-hot类型向量
维的one-hot类型向量![]() 来表示多分类任务中的类别标签。对于类别
来表示多分类任务中的类别标签。对于类别![]() ,其向量表示为:
,其向量表示为:
![]()
其中![]() 是指示函数,即括号内的输入为“真”,
是指示函数,即括号内的输入为“真”,![]() ;否则,
;否则,![]() 。
。
给定有![]() 个训练样本的训练集
个训练样本的训练集![]() ,令
,令![]() 为样本
为样本![]() 在每个类别的后验概率。多分类问题的交叉熵损失函数定义为:
在每个类别的后验概率。多分类问题的交叉熵损失函数定义为:
观察上式,![]() 在
在![]() 为真实类别时为1,其余都为0。也就是说,交叉熵损失只关心正确类别的预测概率,因此,上式又可以优化为:
为真实类别时为1,其余都为0。也就是说,交叉熵损失只关心正确类别的预测概率,因此,上式又可以优化为:
其中![]() 是第
是第![]() 个样本的标签。
个样本的标签。
因此,多类交叉熵损失函数的代码实现如下:
class MultiCrossEntropyLoss(Op):
def __init__(self):
self.predicts = None
self.labels = None
self.num = None
def __call__(self, predicts, labels):
return self.forward(predicts, labels)
def forward(self, predicts, labels):
"""
输入:
- predicts:预测值,shape=[N, 1],N为样本数量
- labels:真实标签,shape=[N, 1]
输出:
- 损失值:shape=[1]
"""
self.predicts = predicts
self.labels = labels
self.num = self.predicts.shape[0]
loss = 0
for i in range(0, self.num):
index = self.labels[i]
loss -= torch.log(self.predicts[i][index])
return loss / self.num
# 测试一下
# 假设真实标签为第1类
labels = paddle.to_tensor([0])
# 计算风险函数
mce_loss = MultiCrossEntropyLoss()
print(mce_loss(outputs, labels))运行结果如下:
4.模型优化
计算风险函数![]() 关于参数
关于参数![]() 和
和![]() 的偏导数。在Softmax回归中,计算方法为:
的偏导数。在Softmax回归中,计算方法为:
![]()
其中![]() 为
为![]() 个样本组成的矩阵,
个样本组成的矩阵,![]() 为
为![]() 个样本标签组成的向量,
个样本标签组成的向量,![]() 为
为![]() 个样本的预测标签组成的向量,
个样本的预测标签组成的向量,![]() 为
为![]() 维的全1向量。
维的全1向量。
将上述计算方法定义在模型的backward函数中,代码实现如下:
class model_SR(Op):
def __init__(self, input_dim, output_dim):
super(model_SR, self).__init__()
self.params = {}
#将线性层的权重参数全部初始化为0
self.params['W'] = torch.zeros((input_dim, output_dim))
#self.params['W'] = paddle.normal(mean=0, std=0.01, shape=[input_dim, output_dim])
#将线性层的偏置参数初始化为0
self.params['b'] = torch.zeros(output_dim)
#存放参数的梯度
self.grads = {}
self.X = None
self.outputs = None
self.output_dim = output_dim
def __call__(self, inputs):
return self.forward(inputs)
def forward(self, inputs):
self.X = inputs
#线性计算
score = torch.matmul(self.X, self.params['W']) + self.params['b']
#Softmax 函数
self.outputs = softmax(score)
return self.outputs
def backward(self, labels):
"""
输入:
- labels:真实标签,shape=[N, 1],其中N为样本数量
"""
#计算偏导数
N =labels.size()[0]
labels = torch.nn.functional.one_hot(labels.to(torch.int64), self.output_dim)
self.grads['W'] = -1 / N * torch.matmul(self.X.t(), (labels-self.outputs))
self.grads['b'] = -1 / N * torch.matmul(torch.ones(N), (labels-self.outputs))5.模型训练
# 特征维度
input_dim = 2
# 类别数
output_dim = 3
# 学习率
lr = 0.1
# 实例化模型
model = model_SR(input_dim=input_dim, output_dim=output_dim)
# 指定优化器
optimizer = SimpleBatchGD(init_lr=lr, model=model)
# 指定损失函数
loss_fn = MultiCrossEntropyLoss()
# 指定评价方式
metric = accuracy
# 实例化RunnerV2类
runner = RunnerV2(model, optimizer, metric, loss_fn)
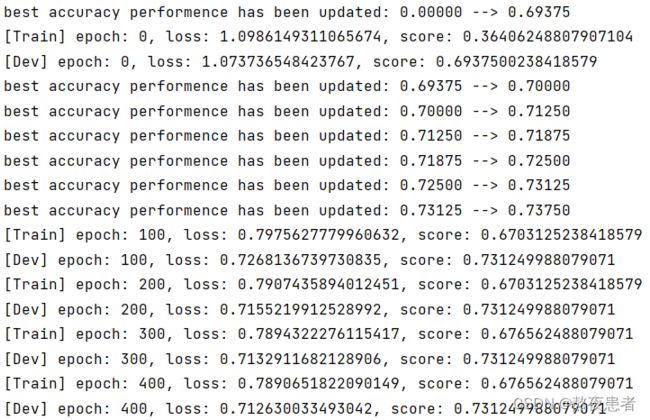
# 模型训练
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=500, log_eopchs=50, eval_epochs=1, save_path="best_model.pdparams")
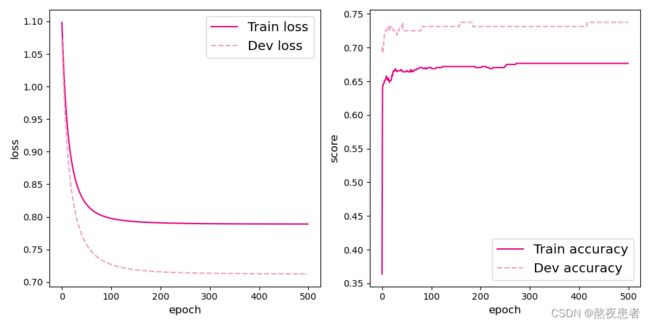
# 可视化观察训练集与验证集的准确率变化情况
plot(runner,fig_name='linear-acc2.pdf')运行结果如下:
6.模型评价
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))运行结果如下:
![]()
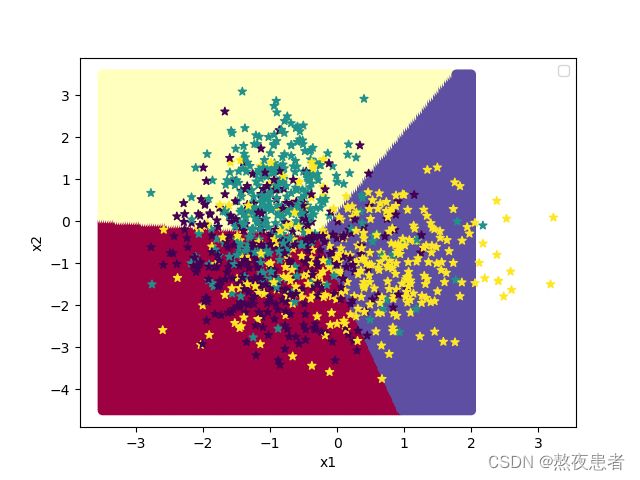
# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-3.5, 2, 200), torch.linspace(-4.5, 3.5, 200))
x = torch.stack([torch.flatten(x1), torch.flatten(x2)], dim=1)
# 预测对应类别
y = runner.predict(x)
y = torch.argmax(y, dim=1)
# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:,0].tolist(), x[:,1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)
n_samples = 1000
X, y = make_multiclass_classification(n_samples=n_samples, n_features=2, n_classes=3, noise=0.2)
plt.scatter(X[:, 0].tolist(), X[:, 1].tolist(), marker='*', c=y.tolist())
plt.legend()
plt.show()运行结果如下:
附录:
main.py
import numpy as np
import torch
import matplotlib.pyplot as plt
from nndl.op import model_SR
from nndl.activation import softmax
from nndl.op import MultiCrossEntropyLoss
from nndl.opitimizer import SimpleBatchGD
from nndl.metric import accuracy
from nndl.runner import RunnerV2
from nndl.tools import plot
def make_multiclass_classification(n_samples=100, n_features=2, n_classes=3, shuffle=True, noise=0.1):
"""
生成带噪音的多类别数据
输入:
- n_samples:数据量大小,数据类型为int
- n_features:特征数量,数据类型为int
- shuffle:是否打乱数据,数据类型为bool
- noise:以多大的程度增加噪声,数据类型为None或float,noise为None时表示不增加噪声
输出:
- X:特征数据,shape=[n_samples,2]
- y:标签数据, shape=[n_samples,1]
"""
# 计算每个类别的样本数量
n_samples_per_class = [int(n_samples / n_classes) for k in range(n_classes)]
for i in range(n_samples - sum(n_samples_per_class)):
n_samples_per_class[i % n_classes] += 1
# 将特征和标签初始化为0
X = torch.zeros((n_samples, n_features))
y = torch.zeros(n_samples, dtype=torch.int32)
# 随机生成3个簇中心作为类别中心
centroids = torch.randperm(2 ** n_features)[:n_classes]
centroids_bin = np.unpackbits(centroids.numpy().astype('uint8')).reshape((-1, 8))[:, -n_features:]
centroids = torch.tensor(centroids_bin, dtype=torch.float32)
# 控制簇中心的分离程度
centroids = 1.5 * centroids - 1
# 随机生成特征值
X[:, :n_features] = torch.randn((n_samples, n_features))
stop = 0
# 将每个类的特征值控制在簇中心附近
for k, centroid in enumerate(centroids):
start, stop = stop, stop + n_samples_per_class[k]
# 指定标签值
y[start:stop] = k % n_classes
X_k = X[start:stop, :n_features]
# 控制每个类别特征值的分散程度
A = 2 * torch.rand(size=(n_features, n_features)) - 1
X_k[...] = torch.matmul(X_k, A)
X_k += centroid
X[start:stop, :n_features] = X_k
# 如果noise不为None,则给特征加入噪声
if noise > 0.0:
# 生成noise掩膜,用来指定给那些样本加入噪声
noise_mask = torch.rand(n_samples) < noise
for i in range(len(noise_mask)):
if noise_mask[i]:
# 给加噪声的样本随机赋标签值
y[i] = torch.randint(n_classes, size=(1,), dtype=torch.int32)
# 如果shuffle为True,将所有数据打乱
if shuffle:
idx = torch.randperm(X.shape[0])
X = X[idx]
y = y[idx]
return X, y
# 采样1000个样本
n_samples = 1000
X, y = make_multiclass_classification(n_samples=n_samples, n_features=2, n_classes=3, noise=0.2)
# 可视化生产的数据集,不同颜色代表不同类别
plt.figure(figsize=(5,5))
plt.scatter(x=X[:, 0].tolist(), y=X[:, 1].tolist(), marker='*', c=y.tolist())
plt.savefig('linear-dataset-vis2.pdf')
plt.show()
num_train = 640
num_dev = 160
num_test = 200
X_train, y_train = X[:num_train], y[:num_train]
X_dev, y_dev = X[num_train:num_train + num_dev], y[num_train:num_train + num_dev]
X_test, y_test = X[num_train + num_dev:], y[num_train + num_dev:]
# 打印X_train和y_train的维度
print("X_train shape: ", X_train.shape, "y_train shape: ", y_train.shape)
# 打印前5个数据的标签
print(y_train[:5])
# 观察softmax的计算方式
X = torch.tensor([[0.1, 0.2, 0.3, 0.4],[1,2,3,4]], dtype=torch.float32)
predict = softmax(X)
print(predict)
# 随机生成1条长度为4的数据
inputs = torch.randn(size=(1, 4))
print('Input is:', inputs)
# 实例化模型,这里令输入长度为4,输出类别数为3
model = model_SR(input_dim=4, output_dim=3)
outputs = model(inputs)
print('Output is:', outputs)
labels = torch.tensor([0])
# 计算风险函数
mce_loss = MultiCrossEntropyLoss()
print(mce_loss(outputs, labels))
# 特征维度
input_dim = 2
# 类别数
output_dim = 3
# 学习率
lr = 0.1
# 实例化模型
model = model_SR(input_dim=input_dim, output_dim=output_dim)
# 指定优化器
optimizer = SimpleBatchGD(init_lr=lr, model=model)
# 指定损失函数
loss_fn = MultiCrossEntropyLoss()
# 指定评价方式
metric = accuracy
# 实例化RunnerV2类
runner = RunnerV2(model, optimizer, metric, loss_fn)
# 模型训练
runner.train([X_train, y_train], [X_dev, y_dev], num_epochs=500, log_eopchs=50, eval_epochs=1, save_path="best_model.pdparams")
# 可视化观察训练集与验证集的准确率变化情况
plot(runner,fig_name='linear-acc2.pdf')
score, loss = runner.evaluate([X_test, y_test])
print("[Test] score/loss: {:.4f}/{:.4f}".format(score, loss))
# 均匀生成40000个数据点
x1, x2 = torch.meshgrid(torch.linspace(-3.5, 2, 200), torch.linspace(-4.5, 3.5, 200))
x = torch.stack([torch.flatten(x1), torch.flatten(x2)], dim=1)
# 预测对应类别
y = runner.predict(x)
y = torch.argmax(y, dim=1)
# 绘制类别区域
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(x[:,0].tolist(), x[:,1].tolist(), c=y.tolist(), cmap=plt.cm.Spectral)
n_samples = 1000
X, y = make_multiclass_classification(n_samples=n_samples, n_features=2, n_classes=3, noise=0.2)
plt.scatter(X[:, 0].tolist(), X[:, 1].tolist(), marker='*', c=y.tolist())
plt.legend()
plt.show()nndl包
op.py
import torch
from DL.实验4_2.nndl.activation import softmax
torch.seed() #设置随机种子
class Op(object):
def __init__(self):
pass
def __call__(self, inputs):
return self.forward(inputs)
def forward(self, inputs):
raise NotImplementedError
def backward(self, inputs):
raise NotImplementedError
# 线性算子
class Linear(Op):
def __init__(self,dimension):
"""
输入:
- dimension:模型要处理的数据特征向量长度
"""
self.dim = dimension
# 模型参数
self.params = {}
self.params['w'] = torch.randn(self.dim,1,dtype=torch.float32)
self.params['b'] = torch.zeros(1,dtype=torch.float32)
def __call__(self, X):
return self.forward(X)
# 前向函数
def forward(self, X):
"""
输入:
- X: tensor, shape=[N,D]
注意这里的X矩阵是由N个x向量的转置拼接成的,与原教材行向量表示方式不一致
输出:
- y_pred: tensor, shape=[N]
"""
N,D = X.shape
if self.dim==0:
return torch.full((N, 1), self.params['b'])
assert D==self.dim # 输入数据维度合法性验证
# 使用paddle.matmul计算两个tensor的乘积
y_pred = torch.matmul(X,self.params['w'])+self.params['b']
return y_pred
#新增Softmax算子
class model_SR(Op):
def __init__(self, input_dim, output_dim):
super(model_SR, self).__init__()
self.params = {}
#将线性层的权重参数全部初始化为0
self.params['W'] = torch.zeros((input_dim, output_dim))
#self.params['W'] = paddle.normal(mean=0, std=0.01, shape=[input_dim, output_dim])
#将线性层的偏置参数初始化为0
self.params['b'] = torch.zeros(output_dim)
#存放参数的梯度
self.grads = {}
self.X = None
self.outputs = None
self.output_dim = output_dim
def __call__(self, inputs):
return self.forward(inputs)
def forward(self, inputs):
self.X = inputs
#线性计算
score = torch.matmul(self.X, self.params['W']) + self.params['b']
#Softmax 函数
self.outputs = softmax(score)
return self.outputs
def backward(self, labels):
"""
输入:
- labels:真实标签,shape=[N, 1],其中N为样本数量
"""
#计算偏导数
N =labels.size()[0]
labels = torch.nn.functional.one_hot(labels.to(torch.int64), self.output_dim)
self.grads['W'] = -1 / N * torch.matmul(self.X.t(), (labels-self.outputs))
self.grads['b'] = -1 / N * torch.matmul(torch.ones(N), (labels-self.outputs))
#新增多类别交叉熵损失
class MultiCrossEntropyLoss(Op):
def __init__(self):
self.predicts = None
self.labels = None
self.num = None
def __call__(self, predicts, labels):
return self.forward(predicts, labels)
def forward(self, predicts, labels):
"""
输入:
- predicts:预测值,shape=[N, 1],N为样本数量
- labels:真实标签,shape=[N, 1]
输出:
- 损失值:shape=[1]
"""
self.predicts = predicts
self.labels = labels
self.num = self.predicts.shape[0]
loss = 0
for i in range(0, self.num):
index = self.labels[i]
loss -= torch.log(self.predicts[i][index])
return loss / self.numactivation.py
import torch
# x为tensor
def softmax(X):
"""
输入:
- X:shape=[N, C],N为向量数量,C为向量维度
"""
x_max = torch.max(X, dim=1, keepdim=True) # N,1
x_exp = torch.exp(X - x_max.values)
partition = torch.sum(x_exp, dim=1, keepdim=True) # N,1
return x_exp / partition
opitimizer.py
import torch
def optimizer_lsm(model, X, y, reg_lambda=0):
"""
输入:
- model: 模型
- X: tensor, 特征数据,shape=[N,D]
- y: tensor,标签数据,shape=[N]
- reg_lambda: float, 正则化系数,默认为0
输出:
- model: 优化好的模型
"""
N, D = X.shape
# 对输入特征数据所有特征向量求平均
x_bar_tran = torch.mean(X,dim=0).T
# 求标签的均值,shape=[1]
y_bar = torch.mean(y)
# paddle.subtract通过广播的方式实现矩阵减向量
x_sub = torch.subtract(X,x_bar_tran)
# 使用paddle.all判断输入tensor是否全0
if torch.all(x_sub==0):
model.params['b'] = y_bar
model.params['w'] = torch.zeros(D)
return model
# paddle.inverse求方阵的逆
tmp = torch.inverse(torch.matmul(x_sub.T,x_sub)+
reg_lambda*torch.eye(D))
w = torch.matmul(torch.matmul(tmp,x_sub.T),(y-y_bar))
b = y_bar-torch.matmul(x_bar_tran,w)
model.params['b'] = b
model.params['w'] = torch.squeeze(w,dim=-1)
return model
from abc import abstractmethod
#新增优化器基类
class Optimizer(object):
def __init__(self, init_lr, model):
"""
优化器类初始化
"""
#初始化学习率,用于参数更新的计算
self.init_lr = init_lr
#指定优化器需要优化的模型
self.model = model
@abstractmethod
def step(self):
"""
定义每次迭代如何更新参数
"""
pass
#新增梯度下降法优化器
class SimpleBatchGD(Optimizer):
def __init__(self, init_lr, model):
super(SimpleBatchGD, self).__init__(init_lr=init_lr, model=model)
def step(self):
#参数更新
#遍历所有参数,按照公式(3.8)和(3.9)更新参数
if isinstance(self.model.params, dict):
for key in self.model.params.keys():
self.model.params[key] = self.model.params[key] - self.init_lr * self.model.grads[key]metric.py
import torch
def accuracy(preds, labels):
"""
输入:
- preds:预测值,二分类时,shape=[N, 1],N为样本数量,多分类时,shape=[N, C],C为类别数量
- labels:真实标签,shape=[N, 1]
输出:
- 准确率:shape=[1]
"""
# 判断是二分类任务还是多分类任务,preds.shape[1]=1时为二分类任务,preds.shape[1]>1时为多分类任务
if preds.shape[1] == 1:
# 二分类时,判断每个概率值是否大于0.5,当大于0.5时,类别为1,否则类别为0
# 使用'torch.gt'比较preds和0.5,返回bool类型的tensor,再使用'torch.float32'将bool类型的tensor转换为float32类型的tensor
preds = torch.gt(preds, 0.5).float()
else:
# 多分类时,使用'torch.argmax'计算最大元素索引作为类别
preds = torch.argmax(preds, dim=1)
return torch.mean((preds == labels).float())runner.py
import torch
# 新增RunnerV2类
class RunnerV2(object):
def __init__(self, model, optimizer, metric, loss_fn):
self.model = model
self.optimizer = optimizer
self.loss_fn = loss_fn
self.metric = metric
# 记录训练过程中的评价指标变化情况
self.train_scores = []
self.dev_scores = []
# 记录训练过程中的损失函数变化情况
self.train_loss = []
self.dev_loss = []
def train(self, train_set, dev_set, **kwargs):
# 传入训练轮数,如果没有传入值则默认为0
num_epochs = kwargs.get("num_epochs", 0)
# 传入log打印频率,如果没有传入值则默认为100
log_epochs = kwargs.get("log_epochs", 100)
# 传入模型保存路径,如果没有传入值则默认为"best_model.pdparams"
save_path = kwargs.get("save_path", "best_model.pdparams")
# 梯度打印函数,如果没有传入则默认为"None"
print_grads = kwargs.get("print_grads", None)
# 记录全局最优指标
best_score = 0
# 进行num_epochs轮训练
for epoch in range(num_epochs):
X, y = train_set
# 获取模型预测
logits = self.model(X)
# 计算交叉熵损失
trn_loss = self.loss_fn(logits, y).item()
self.train_loss.append(trn_loss)
# 计算评价指标
trn_score = self.metric(logits, y).item()
self.train_scores.append(trn_score)
# 计算参数梯度
self.model.backward(y)
if print_grads is not None:
# 打印每一层的梯度
print_grads(self.model)
# 更新模型参数
self.optimizer.step()
dev_score, dev_loss = self.evaluate(dev_set)
# 如果当前指标为最优指标,保存该模型
if dev_score > best_score:
self.save_model(save_path)
print(f"best accuracy performence has been updated: {best_score:.5f} --> {dev_score:.5f}")
best_score = dev_score
if epoch % log_epochs == 0:
print(f"[Train] epoch: {epoch}, loss: {trn_loss}, score: {trn_score}")
print(f"[Dev] epoch: {epoch}, loss: {dev_loss}, score: {dev_score}")
def evaluate(self, data_set):
X, y = data_set
# 计算模型输出
logits = self.model(X)
# 计算损失函数
loss = self.loss_fn(logits, y).item()
self.dev_loss.append(loss)
# 计算评价指标
score = self.metric(logits, y).item()
self.dev_scores.append(score)
return score, loss
def predict(self, X):
return self.model(X)
def save_model(self, save_path):
torch.save(self.model.params, save_path)
def load_model(self, model_path):
self.model.params = torch.load(model_path)tools.py
import matplotlib.pyplot as plt
#新增绘制图像方法
def plot(runner,fig_name):
plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
epochs = [i for i in range(len(runner.train_scores))]
#绘制训练损失变化曲线
plt.plot(epochs, runner.train_loss, color='#e4007f', label="Train loss")
#绘制评价损失变化曲线
plt.plot(epochs, runner.dev_loss, color='#f19ec2', linestyle='--', label="Dev loss")
#绘制坐标轴和图例
plt.ylabel("loss", fontsize='large')
plt.xlabel("epoch", fontsize='large')
plt.legend(loc='upper right', fontsize='x-large')
plt.subplot(1,2,2)
#绘制训练准确率变化曲线
plt.plot(epochs, runner.train_scores, color='#e4007f', label="Train accuracy")
#绘制评价准确率变化曲线
plt.plot(epochs, runner.dev_scores, color='#f19ec2', linestyle='--', label="Dev accuracy")
#绘制坐标轴和图例
plt.ylabel("score", fontsize='large')
plt.xlabel("epoch", fontsize='large')
plt.legend(loc='lower right', fontsize='x-large')
plt.tight_layout()
plt.savefig(fig_name)
plt.show()(PS:累太累了,下次证明少写点,嘤嘤嘤,小公式没给我累死,好处是对softmax有了更深的理解了)