【数据结构与算法python】哈希查找算法的python实现

1、Hashing

在文章《【数据结构与算法python】顺序查找算法的python实现（无序表）》与《【数据结构与算法python】顺序查找算法的python实现（有序表）中，我们利用数据集中关于数据项之间排列关系的知识， 来将查找算法进行了提升，如果数据项之间是按照大小排好序的话，就可以利用二分查找来降低算法复杂度。
为了进一步降低算法的复杂度，构造一个新的数据结构， 能使得查找算法的复杂度降到O(1)， 这种概念称为“哈希Hashing”
能够使得查找的次数降低到常数级别， 我们对数据项所处的位置就必须有更多的先验知识。 如果我们事先能知道要找的数据项应该出现在数据集中的什么位置， 就可以直接到那个位置看看数据项是否存在即可。
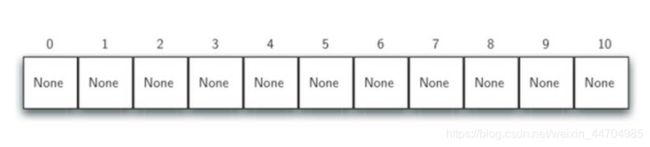
哈希表（hash table， 又称散列表） 是一种数据集， 其中数据项的存储方式尤其有利于将来快速的查找定位。
哈希表中的每一个存储位置， 称为槽（slot） ， 可以用来保存数据项， 每个槽有一个唯一的名称。
例如：一个包含11个槽的哈希表， 槽的名称分别为0～ 10
在插入数据项之前， 每个槽的值都是None， 表示空槽

2、 哈希函数设计

（1）概念

我们引入“ 哈希函数”，用以根据数据项的值来确定其存放位置， 实现从数据项到存储槽名称的转换的， 称为 哈希函数（hash function）。

（2）设计原则

哈希函数不能成为存储过程和查找过程的计算负担，如果哈希函数设计太过复杂， 去花费大量的计算资源计算槽号，可能还不如简单地进行顺序查找或者二分查找，就失去了哈希本身的意义

（3）常用方法

①取余法

有一种常用的散列方法是“求余数”， 将数据项除以散列表的大小， 得到的余数作为槽号。实际上“求余数”方法会以不同形式出现在所有散列函数里，因为散列函数返回的槽号必须在散列表大小范围之内，所以一般会对散列表大小求余。
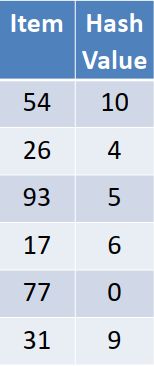
例子： 数据项： 54， 26， 93， 17， 77， 31；槽大小：11
本例中我们的散列函数是最简单的求余：h(item)= item % 11
按照散列函数h(item)，为每个数据项计算出存放的位置之后， 就可以将数
据项存入相应的槽中 ，对应关系如下所示

②折叠法

折叠法设计散列函数的基本步骤是将数据项按照位数分为若干段，
再将几段数字相加，最后对散列表大小求余，得到散列值
例如， 对电话号码62767255，可以两位两位分为4段（62、 76、 72、 55），相加（62+76+72+55=265），散列表包括11个槽，那么就是265%11=1，所以h(62767255)=1

③折叠法（隔数反转 ）

有时候折叠法还会包括一个隔数反转的步骤，比如（62、 76、 72、 55）隔数反转为（62、 67、 72、 55），再累加（62+67+72+55=256），对11求余（256%11=3），所以h’(62767255)=3
虽然隔数反转从理论上看来毫无必要， 但这个步骤确实为折叠法得到散列函数提供了一种微调手段， 以便更好符合散列特性。

④平方取中法

平方取中法， 首先将数据项做平方运算，然后取平方数的中间两位， 再对散列表的大小求余，例如， 对44进行散列，首先44*44=1936，然后取中间的93，对散列表大小11求余， 93%11=5

⑤非数项

我们也可以对非数字的数据项进行散列，把字符串中的每个字符看作ASCII码即可，如cat， ord(‘c’)==99, ord(‘a’)==97,ord(‘t’)==116，再将这些整数累加（99+96+116=212），然后 对散列表大小求余（312%11=4）
当然， 这样的散列函数对所有的变位词（如car和rac，都将返回相同的散列值，为了防止这一点，可以将字符串所在的位置作为权重因子，乘以ord值再相加（（991+962+116*3=641）， 然后对散列表大小求余（641%11=3）

（4）负载因子

槽被数据项占据的比例称为散列表的“负载因子”
例子中的6个数据项插入后， 占据了散列表11个槽中的6个。
这里负载因子为6/11

（5）完美哈希函数

①概念

给定一组数据项， 如果一个哈希函数能把每个数据项映射到不同的槽中， 那么这个哈希函数就可以称为“完美哈希函数”，对于固定的一组数据，总是能想办法设计出完美哈希函数，但如果数据项经常性的变动， 很难有一个
系统性的方法来设计对应的完美散列函数。当然，冲突也不是致命性的错误，我们会有办法处理的。

②设计

获得完美哈希函数的一种方法是扩大哈希表的容量， 大到所有可能出现的数据项都能够占据不同的槽。 但这种方法对于可能数据项范围过大的情
况并不实用假如我们要保存手机号（11位数字），完美哈希函数得要求哈希表具有百亿个槽，会浪费太多存储空间。
好的哈希函数需要具备特性

• 冲突最少（近似完美）
• 计算难度低（额外开销小）
• 充分分散数据项（节约空间）

③用途（数据一致性校验 )

最著名的近似完美哈希函数是MD5和SHA系列函数。
MD5（Message Digest） 将任何长度的数据变换为固定长为128位（16字节）的“摘要” 。
SHA（Secure Hash Algorithm） 是另一组哈希函数。

• SHA-0/SHA-1输出哈希值160位（20字节）
• SHA-256/SHA-224分别输出256位、 224位
• SHA-512/SHA-384分别输出512位和384位

为每个文件计算其哈希值， 仅对比其哈希值即可得知是否文件内容相同，有以下几种用途

• 网络文件下载完整性校验
• 文件分享系统：网盘中相同的文件（尤其是电影） 可以无需存储多次
• 防文件篡改：原理同数据文件一致性判断
• 彩票投注应用：彩民下注前，机构将中奖的结果哈希值公布，然后彩民投注，开奖后，彩民可以通过公布的结果和哈希值对比，验证机构是否作弊。

3、冲突解决方案

（1）概念

如果两个数据项被哈希映射到同一个槽，需要一个系统化的方法在散列表中保存第二个数据项， 这个过程称为“解决冲突” 。
如果说散列函数是完美的， 那就不会有散列冲突， 但完美散列函数常常是不现实的。
解决散列冲突成为散列方法中很重要的一部分。

（2）方法

①开放寻址法（线性探测法）

解决哈希冲突的一种方法就是为冲突的数据项，再找一个开放的空槽来保存。最简单的就是从冲突的槽开始往后扫描，直到碰到一个空槽，如果到散列表尾部还未找到，则从首部接着扫描。这种寻找空槽的技术称为“开放定址法“。向后逐个槽寻找的方法则是开放定址技术中的“线性探测”。
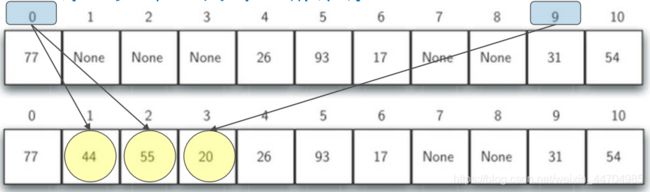
例子：
我们把44、 55、 20逐个插入到散列表中
h(44)=0，但发现0#槽已被77占据，向后找到第一个空槽1#，保存
h(55)=0，同样0#槽已经被占据，向后找到第一个空槽2#，保存
h(20)== 9，发现9#槽已经被31占据了，向后，再从头开始找到3#槽保存

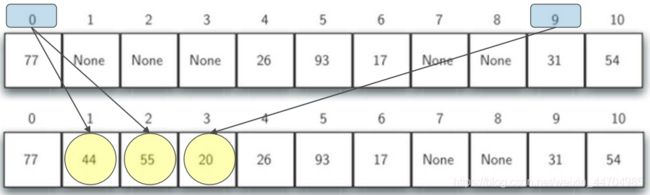
采用线性探测方法来解决散列冲突的话，则散列表的查找也遵循同样的规则
如果在散列位置没有找到查找项的话，就必须向后做顺序查找，直到找到查找项，或者碰到空槽（查找失败）。

②开放寻址法（跳跃式探测）

线性探测法的一个缺点是有聚集 ，即如果同一个槽冲突的数据项较多的话，这些数据项就会在槽附近聚集起来，从而连锁式影响其它数据项的插入。 避免聚集的一种方法就是将线性探测扩展， 从逐个探测改为跳跃式探测。下图是“+3”探测插入44、 55、 20

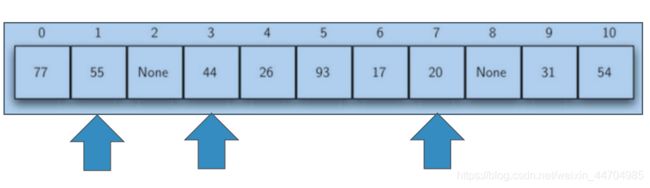
③数据项链

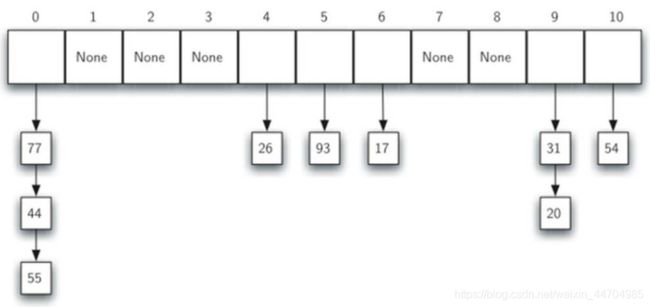
除了寻找空槽的开放定址技术之外， 另一种解决散列冲突的方案是将容纳单个数据项的槽扩展为容纳数据项集合（或者对数据项链表的引用）
这样， 散列表中的每个槽就可以容纳多个数据项， 如果有散列冲突发生， 只需要简单地将数据项添加到数据项集合中。
这样， 散列表中的每个槽就可以容纳多个数据项， 如果有散列冲突发生， 只需要简单地将数据项添加到数据项集合中。

4、代码实现

哈希函数实现方式：取余法
冲突解决方案：开放寻址法

class HashTable:
    def __init__(self):
        self.size = 11
        self.slots = [None] * self.size
        self.data = [None] * self.size
        
    def put(self,key,data):
      hashvalue = self.hashfunction(key,len(self.slots))

      if self.slots[hashvalue] == None:
        self.slots[hashvalue] = key
        self.data[hashvalue] = data
      else:
        if self.slots[hashvalue] == key:
          self.data[hashvalue] = data  #replace
        else:
          nextslot = self.rehash(hashvalue,len(self.slots))
          while self.slots[nextslot] != None and \
                          self.slots[nextslot] != key:
            nextslot = self.rehash(nextslot,len(self.slots))

          if self.slots[nextslot] == None:
            self.slots[nextslot]=key
            self.data[nextslot]=data
          else:
            self.data[nextslot] = data #replace

    def hashfunction(self,key,size):
         return key%size

    def rehash(self,oldhash,size):
        return (oldhash+1)%size
        
    def get(self,key):
      startslot = self.hashfunction(key,len(self.slots))

      data = None
      stop = False
      found = False
      position = startslot
      while self.slots[position] != None and  \
                           not found and not stop:
         if self.slots[position] == key:
           found = True
           data = self.data[position]
         else:
           position=self.rehash(position,len(self.slots))
           if position == startslot:
               stop = True
      return data

    def __getitem__(self,key):
        return self.get(key)

    def __setitem__(self,key,data):
        self.put(key,data)
        
H=HashTable()
H[54]="cat"
H[26]="dog"
H[93]="lion"
H[17]="tiger"
H[77]="bird"
H[31]="cow"
H[44]="goat"
H[55]="pig"
H[20]="chicken"
print(H.slots)
print(H.data)

print(H[20])

print(H[17])
H[20]='duck'
print(H[20])
print(H[99])

5、算法分析

由于数据项都保存到散列表后， 查找就无比简单，要查找某个数据项是否存在于表中， 我们只需要使用同一个散列函数， 对查找项进行计算， 测试下返回的槽号所对应的槽中是否有数据项即可， 实现了O(1)时间复杂度的查找算法。
同时由于散列冲突的存在，查找比较次数就没有这么简单，评估散列冲突的最重要信息就是负载因子λ，
一般来说：
如果λ较小，散列冲突的几率就小，数据项通常会保存在其所属的散列槽中
如果λ较大，意味着散列表填充较满，冲突会越来越多，冲突解决也越复杂，也就需要更多的比较来找到空槽；如果采用数据链的话，意味着每条链上的数据项增多