【1206. 设计跳表】

来源：力扣（LeetCode）

描述：

不使用任何库函数，设计一个 跳表 。
跳表这种数据结构是由 William Pugh 发明的，关于跳表的详细介绍可以参考论文: Skip Lists: A Probabilistic Alternative to Balanced Trees

跳表 是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树，其功能与性能相当，并且跳表的代码长度相较下更短，其设计思想与链表相似。

例如，一个跳表包含 [30, 40, 50, 60, 70, 90] ，然后增加 80、45 到跳表中，以下图的方式操作：

跳表中有很多层，每一层是一个短的链表。在第一层的作用下，增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n))，空间复杂度是 O(n)。

在本题中，你的设计应该要包含这些函数：

• bool search(int target) : 返回 target 是否存在于跳表中。
• void add(int num): 插入一个元素到跳表。
• bool erase(int num): 在跳表中删除一个值，如果 num 不存在，直接返回 false. 如果存在多个 num ，删除其中任意一个即可。

注意，跳表中可能存在多个相同的值，你的代码需要处理这种情况。

示例 1:

输入
["Skiplist", "add", "add", "add", "search", "add", "search", "erase", "erase", "search"]
[[], [1], [2], [3], [0], [4], [1], [0], [1], [1]]
输出
[null, null, null, null, false, null, true, false, true, false]

解释
Skiplist skiplist = new Skiplist();
skiplist.add(1);
skiplist.add(2);
skiplist.add(3);
skiplist.search(0);   // 返回 false
skiplist.add(4);
skiplist.search(1);   // 返回 true
skiplist.erase(0);    // 返回 false，0 不在跳表中
skiplist.erase(1);    // 返回 true
skiplist.search(1);   // 返回 false，1 已被擦除

提示:

• 0 <= num, target <= 2 * 10⁴

• 调用search, add, erase操作次数不大于 5 * 10⁴

方法：直接构造

跳表是一种随机化的数据结构，可以被看做二叉树的一个变种，它在性能上和红黑树、 AVL 树不相上下，但是跳表的原理非常简单，目前在 Redis 和 LevelDB 中都有用到。跳表的期望空间复杂度为 O(n)，跳表的查询，插入和删除操作的期望时间复杂度均为 O(logn)。跳表实际为一种多层的有序链表，跳表的每一层都为一个有序链表，且满足每个位于第 i 层的节点有 pp 的概率出现在第 i + 1 层，其中 p 为常数。

它的结构类似于如下图所示:

跳表在进行查找时，首先从当前的最高层 L(n) 层开始查找，在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层进行查找，重复这个过程直至到达第一层。此时，若下一个节点是目标节点，则成功查找；反之，则元素不存在。由于从高层往低层开始查找，由于低层出现的元素可能不会出现在高层，因此跳表在进行查找的过程中会跳过一些元素，相比于有序链表的查询，跳表的查询速度会更快。
跳表的初始化、查找、添加、删除操作详细描述如下：

• search： 从跳表的当前的最大层数 level 层开始查找，在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层进行查找，重复这个过程直至到达第 1 层。此时，若第 1 层的下一个节点的值等于 target，则返回 true；反之，则返回 false。如图所示：
  
• add： 从跳表的当前的最大层数 level 层开始查找，在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层进行查找，重复这个过程直至到达第 1 层。设新加入的节点为 newNode，我们需要计算出此次节点插入的层数 lv，如果 level 小于 lv，则同时需要更新 level。我们用数组 update 保存每一层查找的最后一个节点，第 i 层最后的节点为 update[i]。我们将 newNode 的后续节点指向 update[i] 的下一个节点，同时更新 update[i] 的后续节点为 newNode。如图所示：
  

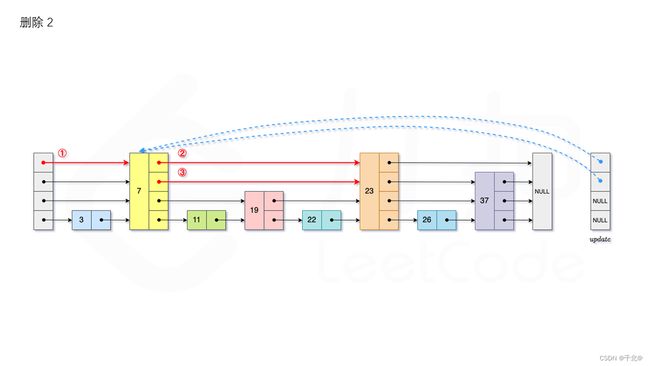
• erase： 首先我们需要查找当前元素是否存在跳表中。从跳表的当前的最大层数 level 层开始查找，在当前层水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层进行查找，重复这个过程直至到达第 1 层。如果第 1 层的下一个节点不等于 num 时，则表示当前元素不存在直接返回。我们用数组 update 保存每一层查找的最后一个节点，第 i 层最后的节点为 update[i]。此时第 i 层的下一个节点的值为 num，则我们需要将其从跳表中将其删除。由于第 i 层的以 p 的概率出现在第 i + 1 层，因此我们应当从第 1 层开始往上进行更新，将 num 从 update[i] 的下一跳中删除，同时更新 update[i] 的后续节点，直到当前层的链表中没有出现 num 的节点为止。最后我们还需要更新跳表中当前的最大层数 level。如图所示：

代码：

constexpr int MAX_LEVEL = 32;
constexpr double P_FACTOR = 0.25;

struct SkiplistNode {
    int val;
    vector<SkiplistNode *> forward;
    SkiplistNode(int _val, int _maxLevel = MAX_LEVEL) : val(_val), forward(_maxLevel, nullptr) {
        
    }
};

class Skiplist {
private:
    SkiplistNode * head;
    int level;
    mt19937 gen{random_device{}()};
    uniform_real_distribution<double> dis;

public:
    Skiplist(): head(new SkiplistNode(-1)), level(0), dis(0, 1) {

    }

    bool search(int target) {
        SkiplistNode *curr = this->head;
        for (int i = level - 1; i >= 0; i--) {
            /* 找到第 i 层小于且最接近 target 的元素*/
            while (curr->forward[i] && curr->forward[i]->val < target) {
                curr = curr->forward[i];
            }
        }
        curr = curr->forward[0];
        /* 检测当前元素的值是否等于 target */
        if (curr && curr->val == target) {
            return true;
        } 
        return false;
    }

    void add(int num) {
        vector<SkiplistNode *> update(MAX_LEVEL, head);
        SkiplistNode *curr = this->head;
        for (int i = level - 1; i >= 0; i--) {
            /* 找到第 i 层小于且最接近 num 的元素*/
            while (curr->forward[i] && curr->forward[i]->val < num) {
                curr = curr->forward[i];
            }
            update[i] = curr;
        }
        int lv = randomLevel();
        level = max(level, lv);
        SkiplistNode *newNode = new SkiplistNode(num, lv);
        for (int i = 0; i < lv; i++) {
            /* 对第 i 层的状态进行更新，将当前元素的 forward 指向新的节点 */
            newNode->forward[i] = update[i]->forward[i];
            update[i]->forward[i] = newNode;
        }
    }

    bool erase(int num) {
        vector<SkiplistNode *> update(MAX_LEVEL, nullptr);
        SkiplistNode *curr = this->head;
        for (int i = level - 1; i >= 0; i--) {
            /* 找到第 i 层小于且最接近 num 的元素*/
            while (curr->forward[i] && curr->forward[i]->val < num) {
                curr = curr->forward[i];
            }
            update[i] = curr;
        }
        curr = curr->forward[0];
        /* 如果值不存在则返回 false */
        if (!curr || curr->val != num) {
            return false;
        }
        for (int i = 0; i < level; i++) {
            if (update[i]->forward[i] != curr) {
                break;
            }
            /* 对第 i 层的状态进行更新，将 forward 指向被删除节点的下一跳 */
            update[i]->forward[i] = curr->forward[i];
        }
        delete curr;
        /* 更新当前的 level */
        while (level > 1 && head->forward[level - 1] == nullptr) {
            level--;
        }
        return true;
    }

    int randomLevel() {
        int lv = 1;
        /* 随机生成 lv */
        while (dis(gen) < P_FACTOR && lv < MAX_LEVEL) {
            lv++;
        }
        return lv;
    }
};

执行用时：68 ms, 在所有 C++ 提交中击败了66.62%的用户
内存消耗：37.4 MB, 在所有 C++ 提交中击败了26.23%的用户
复杂度分析
时间复杂度： O(logn)，其中 n 为 add 的调用次数。详细分析参考题解描述。
空间复杂度： O(n)，其中 n 为 add 的调用次数。详细分析参考题解描述。