02-18 周六 图解机器学习之SMV 第五章5-2
| 时间 | 版本 | 修改人 | 描述 |
|---|---|---|---|
| 2023年2月18日11:47:18 | V0.1 | 宋全恒 | 新建文档 |
环境
程序的基本环境,是使用了jupyter,在容器中运行的。
简介
本程序主要演示支持向量的获取,支持向量是距离超平面最近的点组成的。程序的主要作用是将超平面和支持向量都绘制在同一个图上。
#%程序5-2名称:sklearnsupportvectors.py
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
X, y = make_blobs(n_samples=50, centers=2,random_state=0, cluster_std=0.60)
clf = SVC(kernel='linear')
clf.fit(X, y)
def plot_svc_decision_function(clf, ax=None):
"""Plot the decision function for a 2D SVC"""
if ax is None:
ax = plt.gca()
x = np.linspace(plt.xlim()[0], plt.xlim()[1], 30)
y = np.linspace(plt.ylim()[0], plt.ylim()[1], 30)
Y, X = np.meshgrid(y, x)
P = np.zeros_like(X)
for i, xi in enumerate(x):
for j, yj in enumerate(y):
P[i, j] = clf.decision_function([[xi, yj]])
# plot the margins
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='spring')
plot_svc_decision_function(clf)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
s=200, facecolors='none');
plt.show()
程序解读
数据生成
from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import numpy as np
import matplotlib.pyplot as plt
X, y = make_blobs(n_samples=50, centers=2,random_state=0, cluster_std=0.60)
数据生成,生成的样本数一共50个,中心为2。因为make_blobs默认的参数n_features为2,因此一共有两个特征。
拟合数据
SVM用于分类和回归,目的是找到一个超平面,使得离超平面最近的点都有很大的距离,max(最小距离)。
clf = SVC(kernel='linear')
clf.fit(X, y)
这是重点
clf.support_vectors_[:, 0], clf.support_vectors_[:, 1]这两是支持向量
根据官方code.py,核必须是{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’}之一,或是自定义的。
核函数的选择:
1、特征数量大,和样本数量差不多:此时选LR或者线性核SVM
2、特征数量少,样本数量正常:高斯核
3、特征数量小,样本数量大:手动添加特征变为第一种情况
在本小节生成的程序中,特征数量为2,样本数量为50。差不多一个量级。而且生成的数据是线性可分的。
可以这么理解, 在经过SVM之后,所有与职场向量机相关的数据均封装在了clf对象中了。上述我们打印了clf的支持向量,可以看到一共有三个点是支持向量。
函数定义
def plot_svc_decision_function(clf, ax=None):
"""Plot the decision function for a 2D SVC"""
if ax is None:
ax = plt.gca()
x = np.linspace(plt.xlim()[0], plt.xlim()[1], 30)
y = np.linspace(plt.ylim()[0], plt.ylim()[1], 30)
Y, X = np.meshgrid(y, x)
P = np.zeros_like(X)
for i, xi in enumerate(x):
for j, yj in enumerate(y):
P[i, j] = clf.decision_function([[xi, yj]])
# plot the margins
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
可以看到,在函数定义中传入的参数为clf,classifier的简写。
plt.gca 进行坐标轴的移动
上述在参数中,包含一个ax参数,并且先进行了初始化,意思就是说ax可以由外界传入,如果不传入,我会初始化一个。‘
利用plt.gca进行坐标轴支柱的移动。
上图中,用红色标识出的黑色边界框线在Matplotlib中被称为spines,中文翻译为脊柱…在我理解看来,意思是这些边界框线是坐标轴区域的“支柱”。
那么,我们最终要挪动的其实就是这四个“支柱”
且所有的操作均在plt.gca( )中完成,gca就是get current axes的意思
import matplotlib.pyplot as plt
# 这里建立的画布大小是5*5的,并不是坐标轴范围,使用“十字按钮”拖动你就懂了!
plt.figure(figsize = (5,5))
plt.plot() # 画个只有坐标系的图(因为没有传参数,所以显示空白)
ax = plt.gca()
# 获取你想要挪动的坐标轴,这里只有顶部、底部、左、右四个方向参数
ax.xaxis.set_ticks_position('bottom') # 要挪动底部的X轴,所以先目光锁定底部!
# 在这里,position位置参数有三种,这里用到了“按Y轴刻度位置挪动”
# 'data'表示按数值挪动,其后数字代表挪动到Y轴的刻度值
ax.spines['bottom'].set_position(('data',0))
plt.show()
主要用于进行坐标轴四个支柱的移动。
xlim和ylim
plt.xlim() 显示的是x轴的作图范围,同时plt.ylim() 显示的是y轴的作图范围,而 plt.xticks() 表达的是x轴的刻度内容的范围
可以看出,无参数的xlim默认的范围为从0.01到1.0,通过修改参数进行控制
np.linespace生成等差数列
def linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None):
生成指定范围内指定个数的一维数组
1.在指定的间隔[“start”,“stop”]内均匀地返回数字。
2.返回“num”个等间距的样本。
3.endpoint是一个bool类型的值,如果为"Ture",“stop"是最后一个值,如果为"False”,生成的数组不会包含"stop"值
4.retstep是一个bool类型的值,如果为"Ture",会返回样本之间的间隙。
np.meshgrid(y, x) 用于生成网格矩阵
np.meshgrid(y, x)
X, Y = np.meshgrid(x, y) 代表的是将x中每一个数据和y中每一个数据组合生成很多点,然后将这些点的x坐标放入到X中,y坐标放入Y中,并且相应位置是对应的
nx,ny = (3,2)
#从0开始到1结束,返回一个numpy数组,nx代表数组中元素的个数
x = np.linspace(0,1,nx)
#[ 0. 0.5 1. ]
y = np.linspace(0,1,ny)
# [0. 1.]
xv,yv = np.meshgrid(x,y)
'''
xv
[[ 0. 0.5 1. ]
[ 0. 0.5 1. ]]
yv
[[ 0. 0. 0.]
[ 1. 1. 1.]]
'''
通过上面的例子,其实可以发现meshgrid函数将两个输入的数组x和y进行扩展,前一个的扩展与后一个有关,后一个的扩展与前一个有关,**前一个是竖向扩展,后一个是横向扩展。**因为,y的大小为2,所以x竖向扩展为原来的两倍,而x的大小为3,所以y横向扩展为原来的3倍。通过meshgrid函数之后,输入由原来的数组变成了一个矩阵。通过使用meshgrid函数,可以产生一个表格矩阵
注: meshgrid不仅可以用来生成二维网格,还可以用来生成三维网格。
参见meshgrid生成网格
np.zeros_like(X)
主要用于生成0数组,形状与x相同。
numpy.zeros_like(a, dtype=None, order='K', subok=True, shape=None)[source]
Return an array of zeros with the same shape and type as a given array.
a:array_like
The shape and data-type of a define these same attributes of the returned array.
dtype:data-type, optional
Overrides the data type of the result.
New in version 1.6.0.
order:{‘C’, ‘F’, ‘A’, or ‘K’}, optional
Overrides the memory layout of the result. ‘C’ means C-order, ‘F’ means F-order, ‘A’ means ‘F’ if a is Fortran contiguous, ‘C’ otherwise. ‘K’ means match the layout of a as closely as possible.
New in version 1.6.0.
subok:bool, optional.
If True, then the newly created array will use the sub-class type of ‘a’, otherwise it will be a base-class array. Defaults to True.
shape:int or sequence of ints, optional.
Overrides the shape of the result. If order=’K’ and the number of dimensions is unchanged, will try to keep order, otherwise, order=’C’ is implied.
演示理解:
>>> x = np.arange(6)
>>> x = x.reshape((2, 3))
>>> x
array([[0, 1, 2],
[3, 4, 5]])
>>> np.zeros_like(x)
array([[0, 0, 0],
[0, 0, 0]])
>>> y = np.arange(3, dtype=float)
>>> y
array([0., 1., 2.])
>>> np.zeros_like(y)
array([0., 0., 0.])
enumerate 枚举列表
enumerate在字典赏识枚举、列举的意思;
enumerate参数为可遍历/可迭代的对象(如列表、字符串);
enumerate多用于在for循环中得到计数,利用它可以同时获得索引和值,即需要 index 和 value 值的时候可以使用enumerate;
enumerate()返回的是一个enumerate对象 。
s = [1, 2, 3, 4, 5]
e = enumerate(s)
print(e)
# 示例: 索引从0开始。
s = [1, 2, 3, 4, 5]
x = enumerate(s)
for index,value in x:
print("%s,%s"%(index,value))
# 0,1
# 1,2
# 2,3
# 3,4
# 4,5
示例: 索引从1开始
s = [1, 2, 3, 4, 5]
# 索引从1开始
for index,value in enumerate(s, 1):
print("%s,%s" %(index,value))
# 1,1
# 2,2
# 3,3
# 4,4
# 5,5
示例: 将一组字典列表中的某一对字典元素与另一组字典列表中某一对字典元素组成一组新的字典列表
notes = [{'id': '11111111111', 'content': 'lalallalalalallala'}, {'id': '2222222222222', 'content': 'qqqqqqqqqqqqqqqqqqq'}, {'id': '33333333333333333', 'content': 'aaaaaaaaaaaaaaaaa'}]
ids = [one_note["id"] for one_note in notes]
contents = [one_note["content"] for one_note in notes]
print(type(ids)) # 注: index, label in enumerate(result),其中每次index为序号0,lable,为每个字典。
clf.decision_function()
def plot_svc_decision_function(clf, ax=None):
"""Plot the decision function for a 2D SVC"""
if ax is None:
ax = plt.gca()
x = np.linspace(plt.xlim()[0], plt.xlim()[1], 30)
y = np.linspace(plt.ylim()[0], plt.ylim()[1], 30)
Y, X = np.meshgrid(y, x)
P = np.zeros_like(X)
for i, xi in enumerate(x):
for j, yj in enumerate(y):
P[i, j] = clf.decision_function([[xi, yj]])
# plot the margins
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
没看懂,参见 scikit-learn工具包中分类模型predict_proba、predict、decision_function用法详解
- classes_属性按顺序保存着训练样本的类别标记。
- predict_proba: 模型预测输入样本属于每种类别的概率,概率和为1,每个位置的概率分别对应classes_中对应位置的类别标签。以上述类别标签为[2 4 6 8]的那个分类器为例,查看一下分类模型预测的概率。

输入的[-1, -1]刚好是训练分类器时使用的数据,训练数据中[-1, -1]属于类别6,在predict_proba输出概率中,最大概率值出现在第三个位置上,第三个位置对应的classes_类别刚好也是类别6。这也就是说,predict_proba输出概率最大值索引位置对应的classes_元素就是样本所属的类别。下面就来看一下predict的预测结果与predict_proba的预测结果是否一致。
- predict:模型预测输入样本所述的类别,是则输出1,不是则输出0.
在上一步中知道了predict_proba是输出样本属于各个类别的概率,且取概率最大的类别作为样本的预测结果,下面看一下predict的预测结果与predict_proba的最大值是否一致。
![]()
predict的预测结果为类别6,对应于classes_中的第三个元素,也同时对应于predict_proba中的第三个元素,且是概率值最大的元素
- decision_functinon
The confidence score for a sample is the signed distance of that sample to the hyperplane.
![]()
说了两件事情,其一是说评估样本X的的decision_function(等于没说,哈哈哈),其二是说,如果decision_dunction_shape**=‘ovr’,则输出的decison_function形状是(n_samples, n_classes)**, n_samples是输入样本的数量,n_classes是训练样本的类别数。这里再补充一点,如果decision_dunction_shape='ovo,则输出的decison_function形状是(n_samples, n_classes * (n_classes - 1) / 2)。‘ovr’和‘ovo’又是啥?莫急,莫急。暂且知道是用于训练多分类的就行。
大致解释下decison_function就是用来衡量待预测样本到分类模型各个分隔超平面的距离(没找到太直观的解释方法)。
我们常见的分类器,比如LR和SVM都是只能支持二分类的,回想一下LR分类器,通过判断线性模型的预测结果是否大于0,进而判断sigmoid的输出结果是否大于0.5来判断模型属于正类还是负类。SVM也一样,前面讲了,SVM通过分隔超平面将样本分到两边去,也就是进行二分类。那么怎么能将二分类的分类算法应用到多分类任务上去呢?这就是‘ovr’和‘ovo’要解决的问题。
-
‘ovr’:全称是One-vs-Rest。就是一个人和对面一群人干一次架(群殴)。假如我们训练数据中包含[0, 1, 2, 3]四个分类,那么分别将0, 1, 2, 3作为正样本,其余的123, 023, 013, 012作为负样本(理解: 分解就是0为正类,123为负类,1为正类,023为负类依次类推。),训练4个分类器,每个分类器预测的结果表示属于对应正类也就是0, 1, 2, 3 的概率。这样对于一个输入样本就相当于要进行4个二分类,然后取输出结果最大的数值对应的classes_类别。
-
‘ovo’:全称是One-vs-One。就是一个人分别和对面的每个人干一次架(单挑,车轮战术)。同样,假如我们训练数据中包含[0, 1, 2, 3]四个分类,先将类别0作为正样本,类别1,类别2,类别3依次作为负样本训练3个分类器(理解: 0为正,1,2,3为负,训练3个分类器),然后以类别1为正样本,类别0,类别2, 类别3作为负样本训练3个分类器,以此类推。由于类别0为正样本,类别1为负样本和类别1为正样本、类别0为负样本实质上是一样的,所以不需要重复训练。
注: 对于ovr不再过多解释,容易理解。
对于ovo,做二分类,0,正, 1, 2, 3 负类,这样就是3种情况即01, 02, 03
1正, 0, 2,3为负 又是三种情况(0正1负和0负1正,样本实际是一样的,不再重复训练)。 12, 13
2正, 0,1,2负, 则情况为23.
一共1+2+3 = (4*3)/2
通过上面的描述可知,假如训练样本有n_classes个类别,则’ovr’模式需要训练n_classes个分类器,‘ovo’模式需要训练n_classes * (n_classes - 1) / 2 个分类器。那么问题来了,有多少个分类器是不是就得有多少个分隔超平面,有多少个分隔超平面是不是就得有多少个decision_function值。这也就对应了“他是谁?”那部分所说的decison_function输出形状的描述。
二分类的decision_function
二分类模型中,decision_function返回的数组形状等于样本个数,也就是一个样本返回一个decision_function值。
import numpy as np
from sklearn.svm import SVC
x = np.array([[1,2,3],
[1,3,4],
[2,1,2],
[4,5,6],
[3,5,3],
[1,7,2]])
y = np.array([3, 3, 3, 2, 2, 2])
clf = SVC(probability=True)
clf.fit(x, y)
print(clf.decision_function(x))
# 返回array([2, 3]),其中2为negetive,3为positive
print(clf.classes_)
![]()
还记得前面讲过的decision_function是有符号的吧,大于0表示正样本的可信度大于负样本,否则可信度小于负样本。所以对于前3个样本,decison_function都认为是正样本的可信度高,后3个样本是负样本的可信度高。那么再看一下predict的结果,前3个预测为正样本3(ps:二分类情况下正样本对应的是classes_中的第二个类别),后3个样本预测为负样本2。再看一下predict_proba预测的样本所属的类别概率,可以看到前3个样本属于类别3的概率更大,后3个样本属于类别2的概率更大。
多分类的decision_function
多分类模型中,decision_function返回的数组形状依据使用的模式是**‘ovr’还是‘ovo’**而分别返回n_classes个和n_classes * (n_classes - 1) / 2个数值。
ovr
import matplotlib.pyplot as plt
import numpy as np
from sklearn.svm import SVC
# 样本
X = np.array(
[
[-1, -1],
[-2, -1],
[1, 1],
[2, 1],
[-1, 1],
[-1, 2],
[1, -1],
[1, -2]
]
)
# 类别,一共四类
y = np.array([2, 2, 3, 3, 0, 0, 1, 1])
# SVC多分类模型默认采用ovr模式
clf = SVC(probability=True, decision_function_shape="ovr")
clf.fit(X, y)
# 计算样本距离每个分类边界的距离
# One-vs-One 按照decision_function的得分[01, 02, 03, 12, 13, 23]判断每个分类器的分类结果,然后进行投票
# One-vs-Rest 选择decision_function的得分[0-Rest, 1-Rest, 2-Rest, 3-Rest]最大的作为分类结果
print("decision_function:\n", clf.decision_function(X))
# precidt预测样本对应的标签类别
print("predict:\n", clf.predict(X))
# predict_proba 预测样本对应各个类别的概率
print("predict_proba:\n", clf.predict_proba(X)) #这个是得分,每个分类器的得分,取最大得分对应的类。
print("classes_:", clf.classes_)
在Jupyter中输出如下:
![]()
在ovr场景下,decision_function输出的最大值对应的正样本类别就是decision_function认为置信度最高的预测类别。
ovo
在ovr代码中,只要把代码行
# SVC多分类模型默认采用ovr模式
clf = SVC(probability=True, decision_function_shape="ovo")
clf.fit(X, y)
即可将分类器转换为ovo模式。
模型在训练集上的decision_function以及predict_procaba、predict结果如下:
![]()
ovo模式下,4个类别的训练数据,需要训练6个二分类器,得到6个decition_function值,依照classes_的类别顺序,6个二分类器分别是[01, 02, 03, 12, 13, 23],前面的数字表示正类,后面的表示负类。以decision_function的第一行输出结果为例:
-0.07609727 对应 01分类器,且数值小于0,则分类结果为后者,即类别1
-1.00023294 对应 02分类器,且数值小于0,则分类结果为后者,即类别2
0.27849207 对应 03分类器,且数值大于0,则分类结果为前者,即类别0
-0.834258626 对应 12分类器,且数值小于0,则分类结果为后者,即类别2
0.24756982 对应 13分类器,且数值大于0,则分类结果为前者,即类别1
1.00006256 对应 23分类器,且数值大于0,则分类结果为前者,即类别2最终得票数:{类别0: 1, 类别1: 2, 类别2: 3, 类别3: 0}
对以上分类结果voting投票,多数获胜,即最终分类结果为类别2。
注: 要理解这个投票的机制,很重要。对于ovo模式,仅仅通过decision_function无法得出最终判定类别。
总结: 通过上面讲的这些大概也能得出decision_function、predict_procaba、predict之间的联系了:
decision_function:输出样本距离各个分类器的分隔超平面的置信度,并由此可以推算出predict的预测结果
predict_procaba:输出样本属于各个类别的概率值,并由此可以推算出predict的预测结果
predict:输出样本属于具体类别的预测结果
还是以SVM分类器为例,SVM分类器有个参数用来控制是否输出预测样本的概率值,probability=True时SVM分类器具有predict_proba函数,可以输出样本的预测概率,但是当probability=False,SVM分类器没有predict_proba函数,也就没办法得到样本预测结果的置信度(简单理解为概率)。但是我们又知道,当我们想要计算分类器的性能时,常常需要用到ROC和AUC,ROC曲线表示分类器预测结果FPR和TPR的变化趋势,AUC表示ROC曲线以下的面积。也就是说,要想得到ROC和AUC,就需要得到一组FPR和TPR,FPR和TPR的计算通常是基于一组样本的预测置信度,分别选择不同的置信度阈值,得到一组FPR和TPR值,然后得到ROC曲线的。现在没有predict_proba就得不到样本预测的置信度。But,还记得我们前面解释decison_function时说过的,**decision_function表示通过度量样本距离分隔超平面距离的来表示置信度。**那么我们是不是可以使用decision_function的置信度来计算ROC呢?答案当然是可以的啦。
ax.contour 绘制等高线
官方文档
contour(z);
contour(x,y,z)
contour(—,levels)
contour(—,ineSpec)
contour(—,Name,Value)
contour(ax,—)
M=contour(—)
[M,C]=contour(__)
contour(Z) 创建一个包含矩阵Z的等值线的等高线图,其中Z包含X-Y平面上的高度值。
contour(X,Y,Z) 指定Z中各值得X和Y坐标。
contour(—,levels) 将要显示得等高线指定为上述任一语法中得最后一个参数。将levels指定为标量n,以在n个自动选择的层级上显示等高线。要在某些特定高度绘制等高线,请将levels指定为单调递增值的向量。
contour(—,LineSpec) 指定等高线的线型和颜色。
contour(—,Name,Value) 使用一个或多个名称—值对组参数指定等高线图的其他选项。
contour(ax,—)在目标坐标区中显示等高线图。将坐标区指定为上述任一语法中的第一个参数。
M=contour(—)返回等高线矩阵M,其中包含每个层级的顶点的(X,Y)坐标。
[M,c]=contour(—)返回等高线矩阵和等高线对象c。显示等高线后使用c设置属性。
参考Python Matplotlib.axes.Axes.contour()用法及代码示例
函数功能:用来绘制等高线和决策边界
参考matplotlib可视化之等高线图plt.contourf()与机器学习中绘制决策边界
参考 网格理解
matplotllib绘图,值得认真查看,有代码有图,对于熟悉matplot的库由许多帮助。
contour理解
python 等高线与等高线填充图 较为准确的。
contour函数用于绘制等高线和等高线之间的填充,等高线的理解就是对于一个函数,等高线就是假如有一个函数z=f(x,y),你在平面上所有的x,y取值都会对应一个z值,如果f是连续的,那么把z值相同的点(x,y)连接起来就会形成一条曲线,这就是这个z值的等高线。等高线的理解参见
等高线
def plot_svc_decision_function(clf, ax=None):
"""Plot the decision function for a 2D SVC"""
if ax is None:
ax = plt.gca()
x = np.linspace(plt.xlim()[0], plt.xlim()[1], 30)
y = np.linspace(plt.ylim()[0], plt.ylim()[1], 30)
Y, X = np.meshgrid(y, x)
P = np.zeros_like(X)
for i, xi in enumerate(x):
for j, yj in enumerate(y):
P[i, j] = clf.decision_function([[xi, yj]])
# plot the margins
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
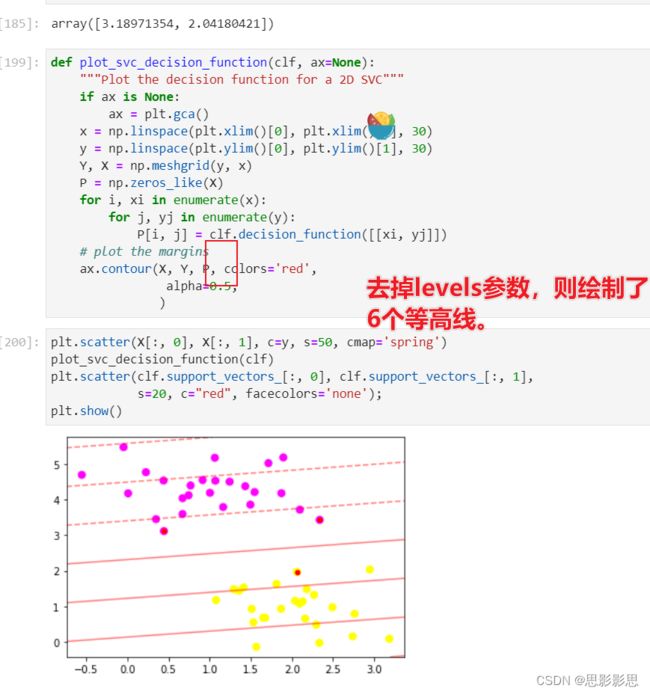
绘制等高线,levels表示要关注的高度值。linestyles则可以取值实线,点斜线,点线等。把levels修改为[-1, 0, 1, 2]则会出现四根线。
8.Matplotlib绘图–等高线
绘制散点图
scatter文档参考
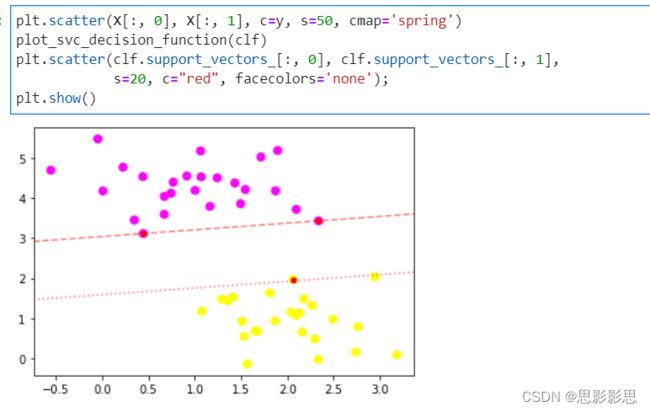
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='spring')
plot_svc_decision_function(clf)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
s=2000, facecolors='none');
plt.show()
从上图中可以看出,c用于表示点的颜色。在进行支持向量的绘制的时候,描述了所有的点。
因此,我觉得在绘制等高线时,matplot应该是对网格内进行了插值,插入了许多点来进行绘制等高线。网格仅用来圈定散点的范围。二维上的许多特征点,也可以理解在高纬空间中,只不过恰好在同一个平面上而已。绘制散点图的工作就不做进一步分析了,因为之前已经总结过了。
总结
图解机器学习这个书呢,自己也是痛苦了许久,因为情绪也不怎么好吧,所以自我提升也一直没有不愿意开展。刚刚完成了对于甘地自传的阅读,接下来就是希望3月份能完成这本《图解机器学习》的阅读。
本文中对于ovo和ovr的理解还是很重要的。发现虽然是尝试理解机器学习,但是好像都是在熟悉sklearn和matplot,画图和机器学习,算法也都封装好了。先会用再说吧。
参考支持向量机代码实现_sklearn实现支持向量机