Graph Attention Networks翻译
论文
这是一篇将attention机制应用到graph convolution中的文章。但是文章中提出的模型其实是利用了attention的一部分思想，和处理sequence的模型应用的attention机制是不完全一样的。
处理sequence的模型引入的attention机制可以分为两类，一类是在输入sequence本身上计算attention的intertext情形；另一类是另外有一个用来计算attention的文本的intertext情形 。本文中的情形是intratext，是在输入的待处理的graph自身上计算attention，在摘要中作者说明了，本文的attention计算的目的是为每个节点neighborhood中的节点分配不同的权重，也就是attention是用来关注那些作用比较大的节点，而忽视一些作用较小的节点。相比之下，在sequence的模型中，attention的计算是为了在处理局部信息的时候同时能够关注整体的信息，计算出来的attention不是用来给参与计算的各个节点进行加权的，而是表示一个全局的信息并参与计算。
Abstract
本文提出了一种新的应用于图数据上的网络结果Graph Attention Networks(GATs)，不同于先前一些基于谱域的图神经网络，通过使用masked的self attention，从而克服了先前图卷积网络或其近似的现有方法的缺点。通过堆叠节点能够参与其邻域特征的层layers，我们（隐式地）为邻域中的不同节点指定了不同的权重，而无需任何类型的计算密集型矩阵运算（如求逆）或依赖于图结构。通过这种方式，我们可以同时解决基于频谱的图神经网络的几个关键挑战，并使我们的模型易于适用于归纳（inductive problems）和推理问题（transductive problems）。我们的GAT模型已在四个已建立的transductive and inductive graph benchmarks中达到或匹配了最先进的结果：the Cora, Citeseer and Pubmed citation network datasets, as well as a protein-protein interaction dataset(其中训练时测试图仍然不可见）。
这里插播一下inductive problems和transductive problems： 主要区别是在，训练阶段是否利用了Test data：
- Inductive learning对未来的Testing data并不知，Transductive
- learning则是已知Testing data的，当然Testing data是unlabeled。
1、Introduction
这部分分析了从CNN到GNN的发展历程，然后分别剖析了现有基于谱域的GNN方法和非谱域GNN方法的不足之处。
- 首先指出，许多有趣的任务涉及无法以网格状结构表示的数据，而这些数据位于不规则的域中。 3D网格，社交网络，电信网络，生物网络或大脑连接组就是这种情况。 此类数据通常可以以图形的形式表示。
- 其次说，基于谱域的GNN不断进化，通过在傅利叶定义域内对图上拉普拉斯算子进行特征分解来实现卷积操作，再到引入平滑参数的filter，再到通过图的切比雪夫展开的filter，最后是限制只对一阶邻居进行操作的方法。所有这些方法都要依靠拉普拉斯矩阵的特征值，这就必须对整个图结构进行操作，这就使得一个训练好的模型很难适用于其他问题。
- 对于非谱域的方法，即空域上的GNN方法，通过对空间中邻居节点进行卷积操作是一个方法，但是这需要解决如何处理不同节点不一样的邻居数目。一些方法是使用图的度矩阵作为输入，或者固定邻居节点的数量。
接着，论文介绍了一下Attention mechanism。注意力机制在许多基于序列的任务中几乎已经成为事实上的标准（Bah-danau等人，2015； Gehring等人，2016）。 注意力机制的好处之一是，它们允许处理可变大小的输入，着眼于输入中最相关的部分以做出决策。 当注意力机制用于计算单个序列的表示时，通常称为自我注意力或内部注意力（When an attention mechanism is used to compute a representation of a single sequence, it is commonly referred to as self-attention or intra-attention）。 自注意力与循环神经网络（RNN）或卷积一起，已被证明对诸如机器阅读（Cheng等人，2016）和学习句子表示（Lin等人，2017）之类的任务很有用。 但是，Vaswani等人（2017）表明，自我注意力不仅可以改善基于RNN或卷积的方法，而且足以构建一个强大的模型，从而获得机器翻译任务的最新性能。
基于以上的工作，受到attention mechanism的启发，我们也要提出一个attention based的模型，在graph structured data上进行节点分类的任务。想法是为每一个节点更新hidden representation的时候，都要对其neighbors进行一下attention（注意力值）的计算，模仿sequence based task中的intratext的attention的思想。作者指出这个注意力框架有三个特点：
- 1、attention机制计算很高效，为每一个节点和其每个近邻节点计算attention可以并行进行。
(并行处理节点-邻居节点对) - 2、通过指定任意的权重给neighbor，这个模型可以处理拥有不同“度”（每个节点连接的其他节点的数目）节点，也就是说，无论一个节点连接多少个neighbor，这个模型都能按照规则指定权重。
(可以处理有不同度节点) - 3、这个模型可以直接应用到归纳推理的问题中（inductive learning problem），包括一些需要将模型推广到完全未知的graph的任务中。
(该模型是inductive的，即不需要知道整个图的全部信息)
作者在四个数据集上进行了实验都取得了state-of-the-art的结果。这四个数据集，三个是引用文献的，一个是蛋白质相互作用网络的。
作者在introduction的后面提到，本文的工作可以看做是MoNet的具体形式，并且在不同edge上共享计算网络很像Santoro 2017年的relational networks和Hoshen 2017年的VAIN，之后还简单提到了一些其他的相关工作。
2、GAT Architecture
2.1 Graph Attentional Layer
模型的输入是node feature的集合，即 h = { h ⃗ 1 , h ⃗ 2 , … , h ⃗ N } , h ⃗ i ∈ R F \mathbf{h}=\left\{\vec{h}_{1}, \vec{h}_{2}, \ldots, \vec{h}_{N}\right\}, \vec{h}_{i} \in \mathbb{R}^{F} h={h1,h2,…,hN},hi∈RF，其中 N N N是node的数量，F是每一个node的feature数量，其实也就是feature vector的长度。模型的输出也是一个集合 h ′ = { h ⃗ 1 ′ , h ⃗ 2 ′ , … , h ⃗ N ′ } , h ⃗ i ′ ∈ R F ′ \mathbf{h}^{\prime}=\left\{\vec{h}_{1}^{\prime}, \vec{h}_{2}^{\prime}, \ldots, \vec{h}_{N}^{\prime}\right\}, \vec{h}_{i}^{\prime} \in \mathbb{R}^{F^{\prime}} h′={h1′,h2′,…,hN′},hi′∈RF′， N N N是不变的，但是每一个node的feature数量变成了 F ′ F^{\prime} F′，不一定还是之前的 F F F了。node的原始的feature可能不够好用，因此先用至少一层线性层来为每个node计算一个表达能力更强的feature，也即用一个 W ∈ R F ′ × F W \in \mathbb{R}^{F^{\prime}×F} W∈RF′×F应用到每一个node的feature上。之后在node上应用self-attention，这个attention mechanism也是复用的，每个节点都用一样的机制。attention coefficient的计算为 a : R F ′ × R F ′ ⟶ R a:\mathbb{R}^{F^{\prime}}×\mathbb{R}^{F^{\prime}}\longrightarrow \mathbb{R} a:RF′×RF′⟶R，用两个node的feature来计算两个node之间有怎样的一个关系。整个过程便是 e i j = a ( W h i ⃗ , W h j ⃗ ) e_{ij}= a(W\vec{h_i},W\vec{h_j} ) eij=a(Whi,Whj)，即两个node feature先是通过线性变换生成新的表达力更强的feature，然后计算attention coefficient，于是，任意两个node之间都有了attention coefficient，本文的这个attention coefficient其实是用来做加权平均的，即卷积的时候，每个node的更新都是其他node的加权平均（不一定是所有node，本文中实际只用了直接相连的node），但是直接用attention coefficient不太好，因此进行一下softmax，得到 α i j = softmax j ( e i j ) = exp ( e i j ) ∑ k ∈ N i exp ( e i k ) \alpha_{i j}=\operatorname{softmax}_{j}\left(e_{i j}\right)=\frac{\exp \left(e_{i j}\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(e_{i k}\right)} αij=softmaxj(eij)=∑k∈Niexp(eik)exp(eij)，这个系数 α α α就是每次卷积时，用来进行加权求和的系数。以上都是一般性的描述，具体来讲，本文采取的计算attention coefficient的函数 a a a是一个单层的前馈网络，参数是 a ⃗ ∈ R 2 F ′ \vec{a} \in \mathbb{R}^{2F^{\prime}} a∈R2F′，并且使用了LeakyReLU来处理，整个写好就是：
α i j = exp ( Leaky ReLU ( a → T [ W h ⃗ i ∥ W h ⃗ j ] ) ) ∑ k ∈ N i exp ( LeakyReLU ( a → T [ W h ⃗ i ∥ W h ⃗ k ] ) ) \alpha_{i j}=\frac{\exp \left(\text { Leaky ReLU }\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{j}\right]\right)\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(\text { LeakyReLU }\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} \| \mathbf{W} \vec{h}_{k}\right]\right)\right)} αij=∑k∈Niexp( LeakyReLU (aT[Whi∥Whk]))exp( Leaky ReLU (aT[Whi∥Whj]))
其中||表示concate起来。每次卷积时，除了加权求和，还要再弄一个非线性函数，即 h ⃗ i ′ = σ ( ∑ j ∈ N i α i j W h ⃗ j ) \vec{h}_{i}^{\prime}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j} \mathbf{W} \vec{h}_{j}\right) hi′=σ(∑j∈NiαijWhj)。
为了使模型更加稳定，文章还提出了multi-head attention机制，这种机制更加有利，这个意思是说不只用一个函数 a a a进行attention coefficient的计算，而是设置K个函数，每一个函数都能计算出一组attention coefficient，并能计算出一组加权求和用的系数，每一个卷积层中，K个attention机制独立的工作，分别计算出自己的结果后连接在一起，得到卷积的结果，即：
h ⃗ i ′ = ∏ k = 1 K σ ( ∑ j ∈ N i α i j k W k h ⃗ j ) \vec{h}_{i}^{\prime}=\prod_{k=1}^{K} \sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \vec{h}_{j}\right) hi′=∏k=1Kσ(∑j∈NiαijkWkhj)
||依然表示连接在一起的意思， α i j k \alpha_{ij}^{k} αijk是用第k个计算attention coefficient的函数 ( a k ) (a^{k}) (ak)计算出来的。整个过程如下图所示：
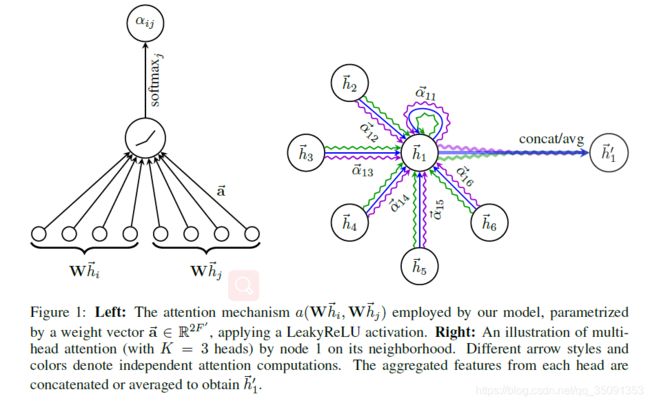对于最后一个卷积层，如果还是使用multi-head attention机制，那么就不采取连接的方式合并不同的attention机制的结果了，而是采用求平均的方式进行处理，即：
h ⃗ i ′ = σ ( 1 K ∑ k = 1 K ∑ j ∈ N i α i j k W k h ⃗ j ) \vec{h}_{i}^{\prime}=\sigma\left(\frac{1}{K} \sum_{k=1}^{K} \sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \vec{h}_{j}\right) hi′=σ(K1∑k=1K∑j∈NiαijkWkhj)
2.2 Comparisons to Related Work
2.1小节中描述的attentional layer直接解决了之前用神经网络建模图结构数据的方法中存在的几个问题，同时也指出在几个方面的优点：
- 计算很高效，attention机制在所有边上的计算是可以并行的，输出的features的计算在所有节点上也可以并行。像特征分解这种非常费资源的操作都不需要。单层的GAT的multi-head的一个head的时间复杂度可以表示为 O ( ∣ V ∣ F F ′ + ∣ E ∣ F ′ ) O(|V|FF^{\prime}+|E|F^{\prime}) O(∣V∣FF′+∣E∣F′)，这里面 ∣ V ∣ F F ′ |V|FF^{\prime} ∣V∣FF′指的应该是计算attention机制的复杂度，每一个节点计算attention coefficient是 O ( F F ′ ) O(FF^{\prime}) O(FF′)，然后每个节点都只计算其与周围几个直接连接的近邻节点之间的coefficient，即 O ( V ) O(V) O(V)，因此整个就是 O ( ∣ V ∣ F F ′ ) O(|V|FF^{\prime}) O(∣V∣FF′)，计算 α α α应该是加上了一个 O ( V ) O(V) O(V)的复杂度。而 ∣ E ∣ F ′ |E|F^{\prime} ∣E∣F′是用来计算卷积的时间复杂度，每个edge都对应将一个node乘上权重并包含到卷积的加权求和中，而每一个node有 F ′ F^{\prime} F′个feature，加进来就是 E E E次操作，因此整个就是 O ( ∣ E ∣ F ′ ) O(|E|F^{\prime}) O(∣E∣F′)的复杂度。这个复杂度和Kipf&Welling 2017年的Graph Convolutional Networks（GCNs）的复杂度相当
- 和GCN不同，本文的模型可以对同一个neighborhood的node分配不同的重要性，使得模型的容量（自由度）大增。并且分析这些学到的attentional weights有利于可解释性（意思可能是分析一下模型在分配不同的权重的时候是从哪些角度着手的），就像机器翻译里的情况（这个其实没看懂是什么意思，作者给了个例子是Bahdanau 2015年的qualitative analysis）
- attention机制是对于所有edge共享的，不需要依赖graph全局的结构以及所有node的特征（很多之前的方法都有这个缺陷，但是作者没有说是什么方法，这种很笼统的话都不太好懂）。这也表明了两点：一是graph不需要是无向的。二是我们的技术适合inductive learning，包括一些任务中，用来测试的graph在训练阶段完全未知（由于本文做的多是在一个大graph上的node分类，因此训练和测试可能是在一个graph上的）。
- 2017年Hamilton提出的inductive method为每一个node都抽取一个固定尺寸的neighborhood，为了计算的时候footprint是一致的（指的应该是计算的时候处理neighborhood的模式是固定的，不好改变，因此每次都抽样出固定数量的neighbor参与计算），这样，在计算的时候就不是所有的neighbor都能参与其中。此外，Hamilton的这个模型在使用一些基于LSTM的方法的时候能得到最好的结果，这样就是假设了每个node的neighborhood的node一直存在着一个顺序，使得这些node成为一个序列。但是本文提出的方法就没有这个问题，每次都可以将neighborhood所有的node都考虑进来，而且不需要事先假定一个neighborhood的顺序
- 这个是说明了之前提到的GAT如何被看做MoNet的一个特例，用到了一些MoNet的东西，需要看一下才知道在说啥。
https://blog.csdn.net/b224618/article/details/81407969