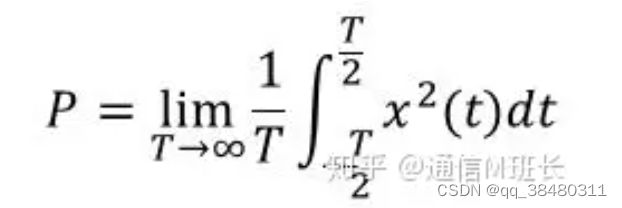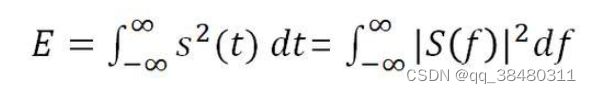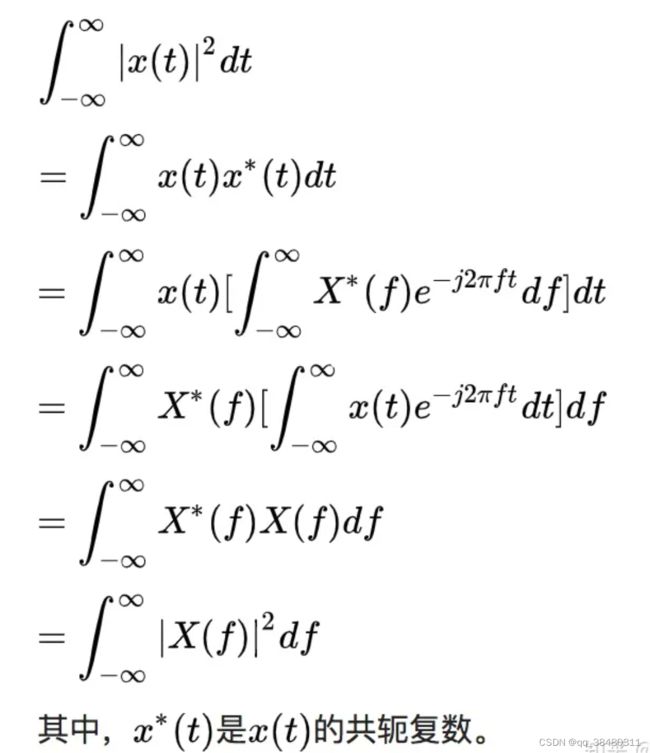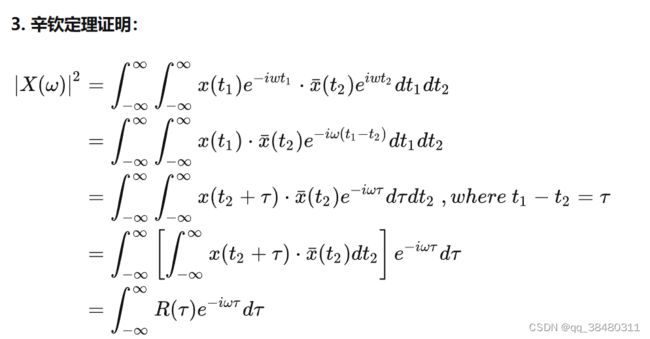如何理解功率谱/能量谱密度？它与自相关函数的关系？

目录

1. 自相关函数：

2.功率谱密度 /能量谱密度

 什么是 能量信号？ 什么是 功率信号？

什么是 能量谱密度？ 什么是 功率谱密度？

3.自相关函数 与 能量谱密度/功率谱密度 的关系？

4.周期性的功率信号的 功率谱是离散的

---

如何理解功率谱密度/能量谱密度？他们与自相关函数的关系？

能量 = 功率 * 时间， 即等于功率在时间上的积分

对于一个能量信号，其 能量 = 能量谱密度 在 谱（即频域）上的积分。可以理解为，信号的能量分布在不同的频率上面，把所有频率上的能量谱 叠加 就得到了 能量。由于 能量信号在 无限长时间内的 能量是一个 有限值 E, 那么其平均功率  应该是一个趋于 0 的值。而功率谱密度是功率 在各个频率上的分量， 总的为0分量自然更为0了， 因而能量信号不存在 功率谱密度，只有能量谱密度。

对于一个功率信号，其 功率 = 能量谱密度 在 谱（即频域）上的积分。可以理解为，信号的功率分布在不同的频率上面，把所有频率上的功率谱 叠加 就得到了 功率。 由于 功率信号在 无限长时间内的 功率是一个 有限值 P, 那么其总能量应该是一个趋于无穷 的值。 因而其没有能量谱密度，只有功率谱密度。

结论： 能量谱密度是

一个能量信号自相关函数的傅里叶变换等价于它的能量谱密度，一个功率信号自相关函数的傅里叶变换等价于它的功率谱密度。  即Wiener-Khinchin theorem。

即 信号的自相关函数与 功率谱/能量谱密度之间成 傅里叶变换对。

请参阅  Wiener-Khinchin theorem - 知乎 (zhihu.com)

想要理解这句话，我们 需要了解 三个名词（自相关函数 & 能量谱密度/功率谱密度），一个操作（傅里叶变换）。 

1. 自相关函数：

 对于一个信号自相关函数的定义：

2.功率谱密度 /能量谱密度

想要理解 功率谱密度 和能量谱 密度的前提是  明白

 什么是 能量信号？ 什么是 功率信号？

请参照 (4 封私信 / 7 条消息) 功率谱密度如何理解？ - 知乎 (zhihu.com)https://www.zhihu.com/question/29520851

要理解 什么是信号的功率？信号的功率定义如下：

为什么这么定义呢？

定义来源于电路的功率计算，但是假设电路的电阻是1 欧姆，在此情况下，

 (因为 )

有了功率的定义，那么怎么计算能量呢？（能量=功率*时间）

如果把T 放宽到无限时间，则 

若第一个极限E存在，即称为能量信号;

若第二个极限P存在，则称为功率信号。

OK，到这里 首先我们 明白了 能量信号和功率信号的含义。 要说明的一点是 一个信号可以既不是能量信号，也不是功率信号，但不可能既是能量信号，又是功率信号。

什么是 能量谱密度？ 什么是 功率谱密度？

由于功率信号具有无穷大的能量，所以按照能量E的公式，这个积分是不存在的。

但是我们可以把这个信号截断成小块。

把信号s(t)截断成一个截短信号sT(t),-T/2

这样sT(t)就是一个能量信号了，我们利用傅里叶变换可以求出其能量谱密度|ST(f)|^2

其中，G（f）是 能量信号的能量谱密度； P（f）是功率信号的功率谱密度。

请仔细看图中的公式， 对于能量信号，求的是 整个时间域上的能量 E，因为在整个时间域上其能量有限，所以是可以求得的； 对于 功率信号，求得是 一个截断时间T的 能量  ET， 因为功率信号在整个时间域上其能量无限，所以是不可以求得的，只能求一个时间内的信号。

对于E/ET，自我理解： 对于 能量等于 功率在 时间域的积分， 也等于 能量谱密度 在 频域的积分。 功率 等于 功率谱密度 在频域上的 积分。

能量是守恒的，不会管你变换来、变换去。所以，不管是在时域还是频域，能量守恒。这也是巴塞伐尔定理。

Parseval's theorem证明：即要证明

从f 或从w 域证明。（）（下图里自行把x（t）当成s（t）即可）

3.自相关函数 与 能量谱密度/功率谱密度 的关系？

对于能量信号：一个能量信号自相关函数的傅里叶变换等价于它的能量谱密度

对于功率信号：一个功率信号自相关函数的傅里叶变换等价于它的功率谱密度

具体证明参照

维纳—辛钦(Winner-Khitchine)定理的证明_维纳辛钦定理_带着地球去浪一浪的博客-CSDN博客

4.周期性的功率信号的 功率谱是离散的

可以将T选作等于信号的周期T0，并且用傅里叶级数代替傅里叶变换，求出信号的频谱

 因为功率信号在时间  T趋近无穷 上的能量是无限的，因而没办法证明其在 无穷时间域的能量 守恒，但是 由于其功率有限，可以证明 其在 时间 域上的平均功率 等于 其 在频域上的（离散）功率谱 相加。

Cn为此周期信号的傅里叶级数的系数。若f0是此信号的基波频率，则Cn是此信号的第n此谐波的振幅；|Cn|^2为第n次谐波的功率，可以称为信号的（离散）功率谱。请注意，这是 功率谱 而非 功率谱密度。 若非是要表示功率谱密度，可以如下定义：

首先，要知道，应用中所说的能量谱==能量谱密度，功率谱≈功率谱密度， 第二，能量信号才有能量谱密度，能量谱密度可由能量信号的傅里叶变换得到，正比于傅里叶谱的平方，能量谱密度对频率积分就可以得到总能量；第三，功率信号包括有周期信号和非周期信号（常见的如随机信号），周期信号可定义功率谱（离散的），正比于傅里叶级数系数的平方，功率谱的累加求和可以得到信号的平均功率，而非周期信号则没有功率谱的概念，这也是功率谱较少使用的原因。通过引入冲击函数，可对周期和非周期的功率信号统一定义功率谱密度，功率谱密度对频率积分就得到信号的平均功率。所以应用中基本只用功率谱密度，也常简称为功率谱。