AI模型评价指标
AI模型评价指标
分类模型评价指标
指标定义
转载:
- Confusion Matrix, Accuracy, Precision, Recall, F1 Score
- What’s a good F1 score?
代码
from sklearn.metrics import precision_score, recall_score, f1_score, accuracy_score, confusion_matrix
def compute_metrics_mutli_cls(y_true, y_pred):
"""
多分类
micro:把所有的类放一起算
macro:先分别求出每个类的precision,再算术平均
weighted: 不再取算术平均,而是乘以该类在总样本数中的占比
:param y_true: 真实label
:param y_pred: 预测label
"""
print("Accuracy:\t{}".format(accuracy_score(y_true, y_pred)))
print("Frecision-micro::\t{}".format(precision_score(y_true, y_pred, average='micro')))
print("Frecision-marco:\t{}".format(precision_score(y_true, y_pred, average='macro')))
print("Frecision-weighted:\t{}".format(precision_score(y_true, y_pred, average='weighted')))
print("Recall-micro: \t{}".format(recall_score(y_true, y_pred,average='micro')))
print("Recal1-marco: \t{}".format(recall_score(y_true, y_pred, average='macro')))
print("Recal1-weighted:\t{}".format(recall_score(y_true, y_pred, average='weighted')))
print("F1-Score-micro:\t{}".format(f1_score(y_true, y_pred, average='micro')))
print("F1-Score-marco:\t{}".format(f1_score(y_true, y_pred, average='macro')))
print("F1-Score-weighted:\t{}".format(f1_score(y_true, y_pred, average='weighted')))
# 混淆矩阵:
print(confusion_matrix(y_true, y_pred))
def compute_metrics_two_cls(y_true, y_pred):
"""
二分类
:param y_true: 真实label
:param y_pred: 预测label
"""
print("Accuracy:\t{}".format(accuracy_score(y_true, y_pred)))
print("Frecision:\t{}".format(precision_score(y_true, y_pred)))
print("Recall: \t{}".format(recall_score(y_true, y_pred)))
print("F1-Score:\t{}".format(f1_score(y_true, y_pred)))
tn, fp, fn, tp = confusion_matrix(test_y, test_predict).ravel()
回归模型评价指标
指标定义
均方根误差(Root Mean Squard Error,RMSE)
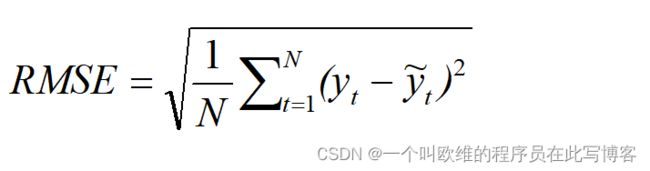
均方根误差RMSE计算的是真实值与预测值之间差值的样本标准差,其计算方式相对均方误差MSE添加了根号,RMSE表明预测的离散程度以及真实值与预测值之间的偏差程度,即预测值在真实回归线附近的分布情况,在构建模型进行非线性拟合时,评价指标均方根误差RMSE值越小越好,但均方根误差容易受到极端值/异常值的影响而产生波动,影响真实评估效果。
平均绝对误差(Mean Absolute Error,MAE)
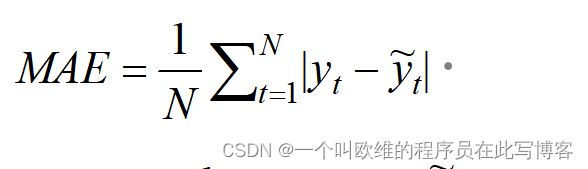
平均绝对误差MAE计算的是真实值与预测值之间绝对误差平均值,其假设所有个体的差异在平均值上的权重是相等的,如RMSE一样,所得值越小表示模型预测误差越小。
平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)
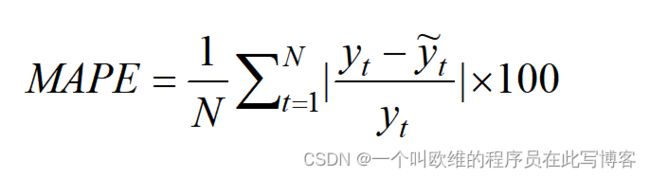
平均绝对百分比误差MAPE表示的是真实值与预测值之间的误差百分比,用于衡量真实观测值和预测值之间的误差程度,该值越小说明预测值接近真实值的程度越高。但MAPE存在一个不足:当预测的真实值很小时,预测后的较小误差将导致MAPE的计算结果增大。
对称平均绝对百分比误差(Symmetric Mean Absolute Percentage Error,SMAPE)
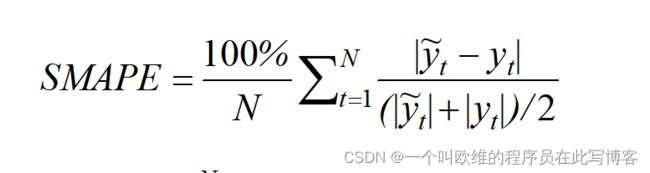
针对MAPE的不足,提出对称平均绝对百分比误差SMAPE进行修正,较好地避免MAPE因预测的真实值过小而导致的SMAPE计算结果较大。
决定系数(Coefficient Of Determination,R Squared)
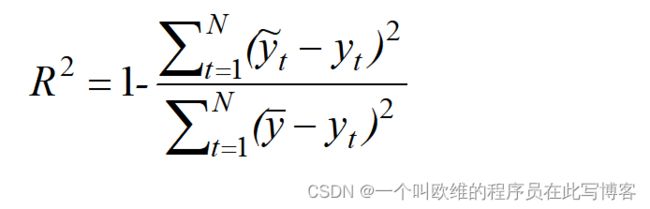
决定系数R Squared反应的是模型对数据样本的拟合程度,预测结果归至[0, 1]之间,值越大表示预测拟合的效果越好。
互相对比
MSE和MAE会由于不同实际应用中,数据的量纲不同,无法直接比较预测值而无法判断模型更适合预测哪个问题。而使用决定系数R Squared可将模型的预测结果转为准确度来衡量,故针对不同的实际应用问题,通过比较预测准确度判断此模型更适合哪个问题。通过上述五种评价指标,可较为全面地、多角度地衡量模型的预测性能。
代码
from sklearn.metrics import mean_squared_error, mean_absolute_error, mean_absolute_percentage_error, r2_score
def regression_evaluation(true_value, pred_value):
"""
回归问题得到预测结果的指标
:param true_value:真实值: np.ndarray
:param pred_value:预测值: np.ndarray
"""
r2 = r2_score(true_value, pred_value)
mae = mean_absolute_error(true_value, pred_value)
rmse = np.sqrt(mean_squared_error(true_value, pred_value))
mse = mean_squared_error(true_value, pred_value)
mape = mean_absolute_percentage_error(true_value, pred_value) * 100
smape = 100 / len(true_value) * np.sum(
2 * np.abs(pred_value - true_value) / (np.abs(true_value) + np.abs(pred_value)))
print("MAE:\t{:.2f}".format(mae))
print("MSE:\t{:.2f}".format(mse))
print("RMSE:\t{:.2f}".format(rmse))
print("R2:\t{:.2f}".format(r2))
print("MAPE:\t{:.2f}".format(mape))
print("SMAPE:\t{:.2f}".format(smape))