布隆过滤器的使用
布隆过滤器简介
Bloom Filter(布隆过滤器)是一种多哈希函数映射的快速查找算法。它是一种空间高效的概率型数据结构,通常应用在一些需要快速判断某个元素是否属于集合,但是并不严格要求100%正确的场合。
布隆过滤器的优势在于,利用很少的空间可以做到精确率较高,空间效率和查询时间都比一般的算法要好的多,缺点是有一定的误识别率和删除困难。为什么不允许删除元素呢:删除意味着需要将对应的 k 个 bits 位置设置为 0,其中有可能是其他元素对应的位。
哈希表与布隆过滤器
哈希表也能用于判断元素是否在集合中,但是Bloom Filter只需要哈希表的1/8或1/4的空间复杂度就能完成同样的问题。Bloom Filter可以插入元素,但是不可以删除已有元素。集合中的元素越多,误报率越大,但是不会漏报。
应用场景
布隆过滤器的用处就是,能够在节省存储空间的情况下迅速判断一个元素是否在一个集合中。主要有如下几个典型使用场景:
- 网页爬虫对URL的去重,避免爬取相同的URL地址;
- 反垃圾邮件,从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱;
- 缓存击穿,将已存在的缓存放到布隆过滤器中,当黑客访问不存在的缓存时迅速返回避免缓存及DB挂掉。
- 黑白名单的过滤
原理
如果想判断一个元素是不是在一个集合中,一般想到的方法是暂存数据,然后查找判定是否存在集合中。这种方法在数据量比较小的情况下适用,但是几个中元素较多的时候,检索速度就会越来越慢。
可以利用Bitmap:只要检查对应点是不是1就可以知道集合中有没有这个数。Bloom filter可以看做是对bitmap的扩展。只是使用多个hash映射函数,从而减低hash发生冲突的概率。可以发现由于有hash的介入,布隆过滤器整体上是一种非常概率的数据结构,存在一定的误判率。所以有这样的特性:key命中了布隆过滤器,代表key可能在布隆过滤器中、key没有命中布隆过滤器,代表key一定不在布隆过滤器中。
在Go 中比较常用的是:https://github.com/bits-and-blooms/bloom,我们可以通过分析这个开源的项目来看下布隆过滤器的实现原理
例子
package main
import (
"fmt"
"github.com/bits-and-blooms/bitset"
bloom "github.com/bits-and-blooms/bloom/v3"
)
func main() {
filter := bloom.NewWithEstimates(1000000, 0.01)
filter.Add([]byte("a"))
if filter.Test([]byte("a")) {
fmt.Println("true")
return
}
fmt.Println("false")
}
数据结构
type BloomFilter struct {
m uint
k uint
b *bitset.BitSet
}
// 这个才是 BloomFilter 真正的底层结构,就是一个 []uint64
type BitSet struct {
length uint
set []uint64
}
// 将元素添加到 布隆过滤器 里面
// Add data to the Bloom Filter. Returns the filter (allows chaining)
func (f *BloomFilter) Add(data []byte) *BloomFilter {
h := baseHashes(data)
for i := uint(0); i < f.k; i++ {
f.b.Set(f.location(h, i))
}
return f
}
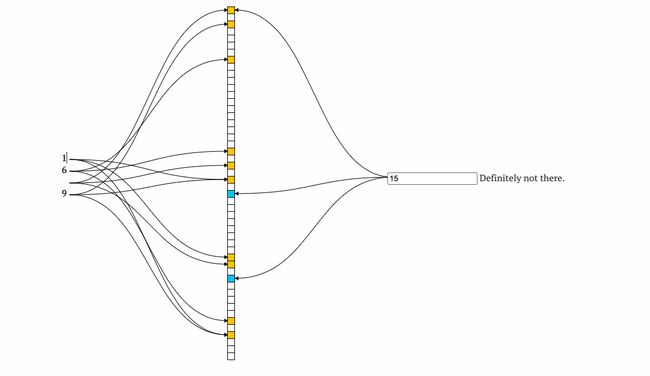
可以简单理解成下面这张图,元素1,6,9 经过 hash 函数之后存在了数组中,在Bloom Filters 可视化网站 可以看到动态视频。然后判断存不存在只需要判断hash 之后的元素对应的数组位置是不是都等于1
问题
布隆过滤器的容量及误判率该如何设定
- 假设布隆过滤器容量为 n,过滤器误判率为 p, qps 为 x,一次请求对布隆过滤器的访问次数为 g,则极限 qps 场景下每秒对布隆过滤器的访问次数为 xg,那每秒可能会有 xg*p 的请求到 数据源中;假设我们的数据源的请求 qps限制 为 y,那么误判率 p 的估计取值为
y / (x*g)。 - 知道了容量和误判率之后,我们就可以通过:https://hur.st/bloomfilter/n=100000000&p=0.0002&m=&k= 大致预估出 布隆过滤器 的大小
如何更新布隆过滤器
因为布隆过滤器不能够删除,所以我们只能定时或者手动更新布隆过滤器
布隆过滤器 Redis 大Key问题
在 n= 1 亿,p=0.0002的数据下,布隆过滤器大概在 211.33MiB,这个时候我们存在redis 上,就会造成 redis 大key 问题,有可能会引起redis 的慢查询,拖挂 redis。
我们可以定时生成布隆过滤器讲结果存储在 DB 或者对象存储中,由每一个服务的实例定时去拉取生成的最新布隆过滤器数据。
Redis布隆过滤器
bitmap
在刚刚我们提到,布隆过滤器的核心数据结构为bitmap, 在Redis上也支持bitmap,其实就是对 string 的每一位进行操作。由此我们也可以得出,用 Redis的bitmap实现的布隆过滤器可以存储最大的数据量为:512x1024x1024x8 = 4294967296,42亿。
我们可以通过 SETBIT 来设置 bit的值,GETBIT 来获取 bit位的值
127.0.0.1:6379> SETBIT mykey 7 1
(integer) 0
127.0.0.1:6379> GETBIT mykey 7
(integer) 1
127.0.0.1:6379> SETBIT mykey 7 0
(integer) 1
127.0.0.1:6379> GETBIT mykey 7
(integer) 0
127.0.0.1:6379>
所以通过Redis bitmap来实现布隆过滤器需要做三件事情:
- k 次散列函数计算出 k 个位点。
- 插入时将位数组中 k 个位点的值设置为 1。
- 查询时根据 1 的计算结果判断 k 位点是否全部为 1,否则表示该元素一定不存在
Bloom Filter
我们也可以通过安装 Redis 的插件:https://github.com/RedisBloom/RedisBloom,这个插件包含了很多数据类型。Bloom filter(布隆过滤器), Cuckoo filter(布谷鸟过滤器), Count-min sketch(频率算法), Top-K, t-digest(近似百分位算法)
在Redis中的操作
bloom filter定义
BF.RESERVE {key} {error_rate} {capacity}
使用给定的期望错误率和初始容量创建空的Bloom过滤器(如果不存在的话)。如果打算向Bloom过滤器中添加许多项,则此命令非常有用,否则只能使用BF.ADD 添加项。
初始容量和错误率将决定过滤器的性能和内存使用情况。一般来说,错误率越小(即对误差的容忍度越低),每个过滤器条目的空间消耗就越大。
bloom filter基本操作
BF.ADD {key} {item}
单条添加元素
向Bloom filter添加一个元素,如果该key不存在,则创建该key(过滤器)。
如果项是新插入的,则为“1”;如果项以前可能存在,则为“0”。
BF.MADD {key} {item} [item…]
批量添加元素
布尔数(整数)的数组。返回值为0或1的范围的数据,这取决于是否将相应的输入元素新添加到过滤器中,或者是否已经存在。
BF.EXISTS {key} {item}
判断单个元素是否存在
如果存在,返回1,否则返回0
BF.MEXISTS {key} {item} [item…]
判断多个元素是否存在
其他相关的命令可以在这里查询到:https://redis.io/commands/?name=bf
127.0.0.1:6379> BF.ADD bfKey 1
(integer) 1
127.0.0.1:6379> BF.ADD bfKey foo
(integer) 1
127.0.0.1:6379> BF.EXISTS bfKey 4
(integer) 0
127.0.0.1:6379> BF.EXISTS bfKey 4
(integer) 0
127.0.0.1:6379> BF.EXISTS bfKey 1
(integer) 1
127.0.0.1:6379> BF.EXISTS bfKey foo
(integer) 1
127.0.0.1:6379>
布谷鸟过滤器
为了解决布隆过滤器中不能删除,且存在误判的缺点,本文引入了一种新的哈希算法——cuckoo filter,它既可以确保该元素存在的必然性,又可以在不违背此前提下删除任意元素,仅仅比bitmap牺牲了微量空间效率。
原理
最简单的布谷鸟哈希结构是一维数组结构,会有两个 hash 算法将新来的元素映射到数组的两个位置。如果两个位置中有一个位置为空,那么就可以将元素直接放进去。但是如果这两个位置都满了,它就不得不「鸠占鹊巢」,随机踢走一个,然后自己霸占了这个位置。
- 使用两个哈希函数 h1(x) 、 h2(x) 和两个哈希桶 T1、T2 。
- 插入元素 x:
- 如果 T1[h1(x)] 、T2[h2(x)] 有一个为空,则插入;两者都空,随便选一个插入。
- 如果 T1[h1(x)] 、T2[h2(x)] 都满,则随便选择其中一个(设为 y ),将其踢出,插入 x。
- 重复上述过程,插入元素 y。
- 如果插入时,踢出次数过多,则说明哈希桶满了。则进行扩容、ReHash 后,再次插入。
- 查询元素 x:
- 读取 T1[h1(x)] 、T2[h2(x)] 和 x 比对即可
可以通过这个Cuckoo Filter 可视化网站观察到。
- 读取 T1[h1(x)] 、T2[h2(x)] 和 x 比对即可
其他
- 布谷鸟哈希
- 布谷鸟过滤器
- 布谷鸟过滤器实现