11.盛最多水的容器

盛最多水的容器

Category	Difficulty	Likes	Dislikes
algorithms	Medium (63.74%)	2707	-

Tags

array | two-pointers

Companies

bloomberg

给你 n 个非负整数 a1，a2，...，a``n，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

**说明：**你不能倾斜容器。

示例 1：

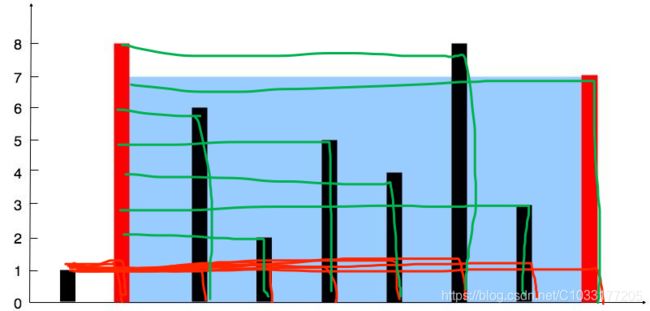
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

示例 3：

输入：height = [4,3,2,1,4]
输出：16

示例 4：

输入：height = [1,2,1]
输出：2

提示：

• n = height.length
• 2 <= n <= 3 * 104
• 0 <= height[i] <= 3 * 104

---

Discussion | Solution

Code Now

思路

真是什么题都想的出来，首先我们看看暴力解法。

暴力解法：

不是求面积么，我们可以从头遍历到尾，然后进行比较那个面积最大，

class Solution {
public:
    int maxArea(vector<int>& height) {
		int N = height.size();
		int area = 0;        
        for(int i=0; i<N; i++)
        {
            for(int j=1; j<N; j++)
            {
                area = max(area, min(height[i], height[j])*(j-i));
            }
        }
        return area;
    }
};

接下来我们来个高级玩法，双指针。

为什么有双指针的思路。我也不知道，看了答案之后，以后就有思路了，不虚。

left = i; right = N-1;

面积S=min(h[left], h[right])*(right-left)

假如：h[left] < h[right]

如果我们这时移动短板，也就是left，移动left在到left+1，会出现h[left+1] > h[left]后者h[left+1] < h[left]，这时候我们代入上面的式子，这时候S移动后的面积可能会变大，也可能会变小。

如果我们这时移动长板，也就是right，移动right到right-1，也会出现h[right-1] > h[left]或者h[right-1] < h[left] （为啥不跟h[right]比较呢，因为跟h[right]比较意义不大）。这时候代入上面的式子，会发现S移动后的面积只能等于或者小于S之前的。

综上所述：需要移动短板的位置。

代码

class Solution {
public:
    int maxArea(vector<int>& height) {
		int N = height.size();
		int area = 0;        
        int left = 0;
        int right = N-1;
        while(left < right)
        {
            area = max(area, min(height[left], height[right])*(right-left));
            if(height[left] < height[right])
            {
                left++;
            } 
            else 
            {
                right--;
            }
        }
        return area;
    }
};